Метод Монте-Карло для решеточного газа Модель решеточного газа. Алгоритм Монте-Карло. Моделирование решеточного газа на двумерно
Содержание
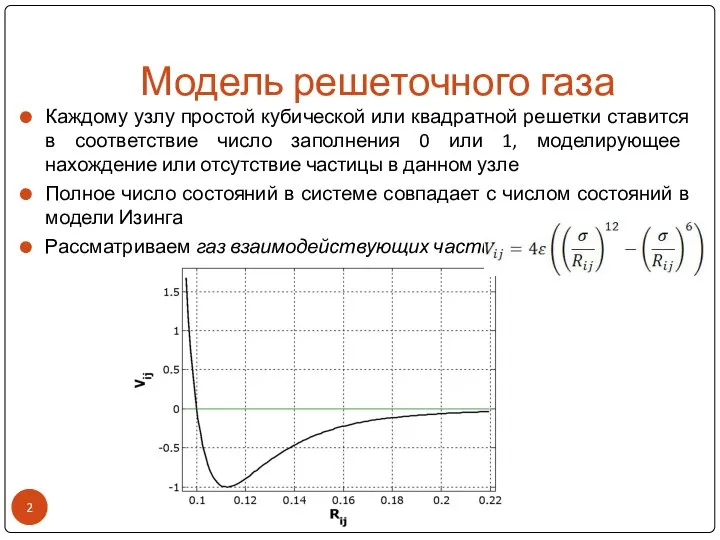
- 2. Модель решеточного газа Каждому узлу простой кубической или квадратной решетки ставится в соответствие число заполнения 0
- 3. Модель решеточного газа на квадратной решетке Точки соответствуют узлам решетки, занятым частицами
- 4. Модель решеточного газа Модельный гамильтониан, описывающий систему: Химический потенциал отвечает переменному числу частиц в системе и
- 5. Алгоритм Монте-Карло Гамильтониан диагонален в базисе чисел заполнения: Необходимо реализовать принцип детального равновесия в условиях большого
- 6. Алгоритм Монте-Карло Процедуры рождения и уничтожения частиц: разные вероятности обращения Уравнение детального баланса: Возможный выбор вероятностей
- 7. Схема алгоритма
- 8. Алгоритм Монте-Карло Число шагов в алгоритме МК определяется достижением необходимой сходимости рассчитываемых величин Для модели решеточного
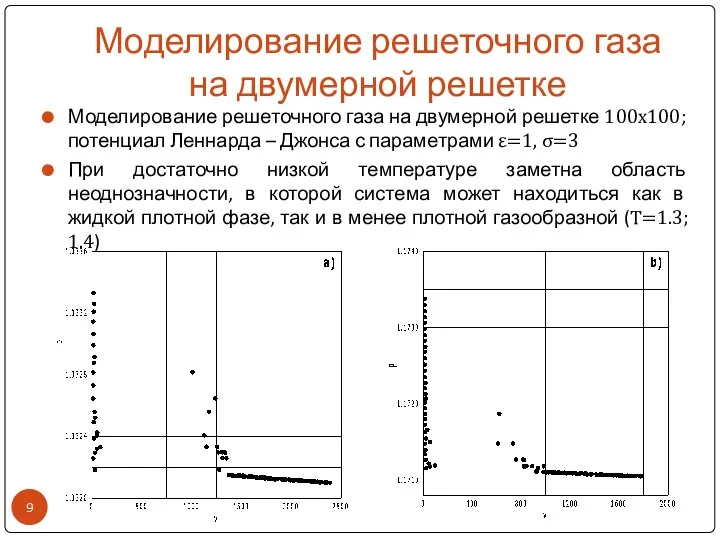
- 9. Моделирование решеточного газа на двумерной решетке Моделирование решеточного газа на двумерной решетке 100х100; потенциал Леннарда –
- 11. Скачать презентацию






 Презентация Диалектика свободы и ответственности
Презентация Диалектика свободы и ответственности  Диск режимов фотоаппарата. Коррекция экспозиции. Экспонометр. Гистограмма. (Занятие 4)
Диск режимов фотоаппарата. Коррекция экспозиции. Экспонометр. Гистограмма. (Занятие 4) Скульптура презентация_
Скульптура презентация_ Презентация на тему "Центр детского творчества "Народные ремёсла" Хабаровск" - скачать презентации по Педагогике
Презентация на тему "Центр детского творчества "Народные ремёсла" Хабаровск" - скачать презентации по Педагогике Внешняя политика Н.С.Хрущёва
Внешняя политика Н.С.Хрущёва Основания по химии
Основания по химии Презентация «Страховой рынок»
Презентация «Страховой рынок» Инсоляция. Актуальность проблемы инсоляции в крупных городах
Инсоляция. Актуальность проблемы инсоляции в крупных городах Основы проектирования туристских комплексов с основами инженерной графики
Основы проектирования туристских комплексов с основами инженерной графики Культурные приложения Мобильные технологии в музеях
Культурные приложения Мобильные технологии в музеях 25يناير في روسيا نحتفل يوم الطالب
25يناير في روسيا نحتفل يوم الطالب По страницам истории школы
По страницам истории школы  Совершенствование регламентации порядка рассмотрения дел об административных правонарушениях мировыми судьями
Совершенствование регламентации порядка рассмотрения дел об административных правонарушениях мировыми судьями Ремонт кофемолки Bosch/Jura
Ремонт кофемолки Bosch/Jura Этика от обезьянок до андроидов
Этика от обезьянок до андроидов Способ крепления балки штырем для фиксации балки в креплении
Способ крепления балки штырем для фиксации балки в креплении Развитие специальной выносливости юных гандболистов на основе применения игрового метода
Развитие специальной выносливости юных гандболистов на основе применения игрового метода Рабочая тетрадь
Рабочая тетрадь Антимикробные свойства текстильных материалов
Антимикробные свойства текстильных материалов Загальна характеристика звукового складу мови. Правила переносу слів
Загальна характеристика звукового складу мови. Правила переносу слів Здоровый образ жизни
Здоровый образ жизни Недостоверное декларирование: не правильное присвоение кода товара по ЕТН ВЭД ТС Выполнили студентки 3-го курса ФТД группы Т-1209
Недостоверное декларирование: не правильное присвоение кода товара по ЕТН ВЭД ТС Выполнили студентки 3-го курса ФТД группы Т-1209  Устойчивость САУ
Устойчивость САУ Характеристика детей, имеющих общее недоразвитие речи - презентация для начальной школы
Характеристика детей, имеющих общее недоразвитие речи - презентация для начальной школы Чарльз Дарвин
Чарльз Дарвин Этические требования к критике
Этические требования к критике Фотосинтез
Фотосинтез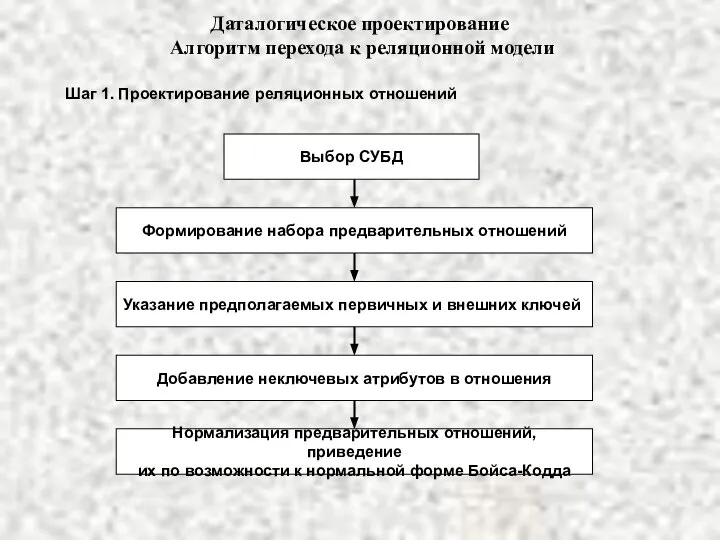 Даталогическое проектирование
Даталогическое проектирование