Тройной интеграл Виды поверхностей второго порядка Замена переменных в тройном интеграле Тройной интеграл в цилиндрических коор
Содержание
- 2. Виды поверхностей второго порядка Цилиндрические поверхности Всякое уравнение, не содержащее переменной z и представляющее на плоскости
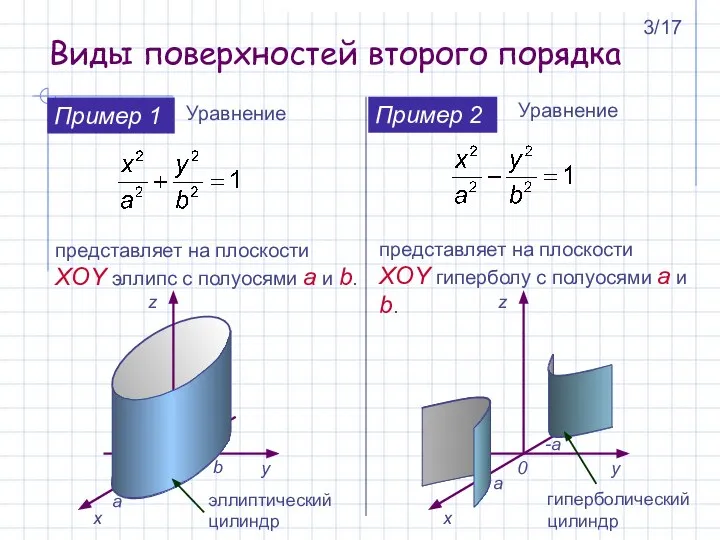
- 3. Виды поверхностей второго порядка Уравнение представляет на плоскости XOY эллипс с полуосями а и b. Пример
- 4. Эти уравнения представляют собой цилиндрические поверхности у которых образующие параллельны осям OY и OX. Уравнение Пример
- 5. Поверхности вращения Уравнение поверхности содержит переменные x и y в виде 2 Для построения этой поверхности
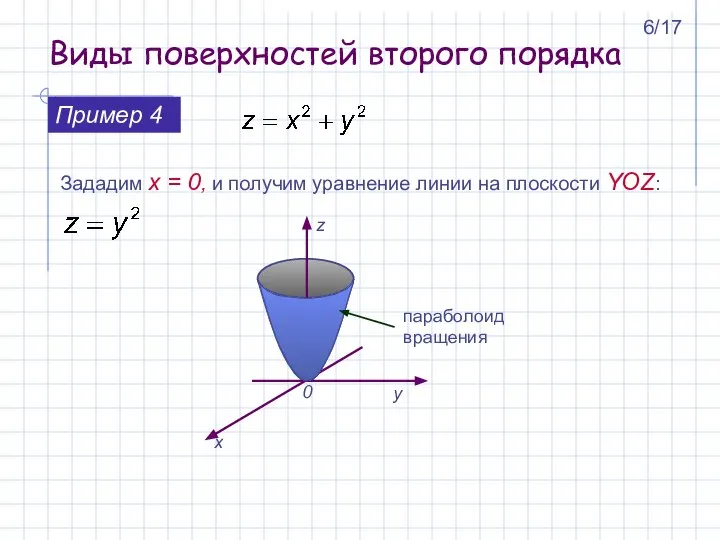
- 6. Зададим x = 0, и получим уравнение линии на плоскости YOZ: Пример 4 параболоид вращения Виды
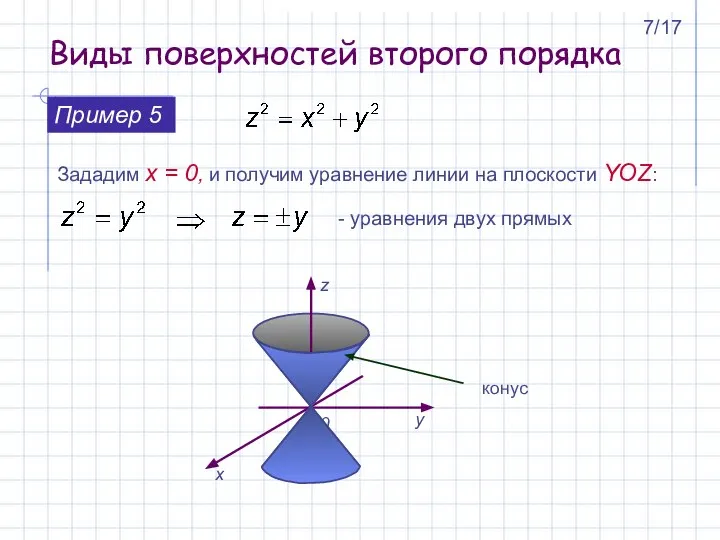
- 7. Зададим x = 0, и получим уравнение линии на плоскости YOZ: Пример 5 конус - уравнения
- 8. Зададим x = 0, и получим уравнение линии на плоскости YOZ: Пример 6 сфера - уравнение
- 9. Замена переменных в тройном интеграле Заменим переменные : определитель Якоби (якобиан) Пусть в замкнутой области V
- 10. Тогда справедлива формула замены переменной в тройном интеграле: Для вычисления тройного интеграла наиболее часто используют так
- 11. Цилиндрические координаты Положение точки M(x; y; z) в пространстве можно определить заданием трех чисел r; φ;
- 12. Цилиндрические координаты точки связаны с ее декартовыми координатами следующими соотношениями: Возьмем в качестве u, v, w
- 13. Формула замены переменных примет вид: Внутренний интеграл берется по переменной z, пределы расставляются также, как в
- 14. К цилиндрическим координатам удобно переходить в том случае, если область D (проекция области V на XOY)
- 15. D z = 1 Приведем уравнение конуса к цилиндрическим координатам: z = r Найдем уравнение линии,
- 16. z = r Расставим пределы интегрирования: r 1 Цилиндрические координаты 0 0 1 16/17
- 18. Скачать презентацию












 Презентация "Презентация на тему: викторина по мультфильмам" - скачать презентации по Экономике
Презентация "Презентация на тему: викторина по мультфильмам" - скачать презентации по Экономике «НОВЫЕ ПОХОЖДЕНИЯ ВЫПУСКНИКОВ, ИЛИ УДИВИТЕЛЬНОЕ ПУТЕШЕСТВИЕ ПО ОКЕАНУ ЗНАНИЙ»
«НОВЫЕ ПОХОЖДЕНИЯ ВЫПУСКНИКОВ, ИЛИ УДИВИТЕЛЬНОЕ ПУТЕШЕСТВИЕ ПО ОКЕАНУ ЗНАНИЙ» Предприятие АО "РКЦ "Прогресс"
Предприятие АО "РКЦ "Прогресс" Я нарисую красками СУДЬБУ
Я нарисую красками СУДЬБУ  ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН: ПСИХОЛОГО-ПЕДАГОГИЧЕСКАЯ ПОДГОТОВКА УЧАЩИХСЯ И РОДИТЕЛЕЙ Барбитова А.Д.
ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН: ПСИХОЛОГО-ПЕДАГОГИЧЕСКАЯ ПОДГОТОВКА УЧАЩИХСЯ И РОДИТЕЛЕЙ Барбитова А.Д. Открытие ворот
Открытие ворот Минеральные удобрени - нитраты
Минеральные удобрени - нитраты Системный характер языка. Уровни и единицы языковой системы
Системный характер языка. Уровни и единицы языковой системы Способы измерения бытовой коррупции
Способы измерения бытовой коррупции Презентация по алгебре Теорема синусов
Презентация по алгебре Теорема синусов  Инд генератор
Инд генератор  Вишакха Пуджа
Вишакха Пуджа Примеры торговых марок
Примеры торговых марок Патентоспособность и патентная чистота. Защита прав на ИЗ, ПМ, ПО. Тема 4_Раздел 4 и 5_
Патентоспособность и патентная чистота. Защита прав на ИЗ, ПМ, ПО. Тема 4_Раздел 4 и 5_ Основы деятельности финансового менеджера
Основы деятельности финансового менеджера Протокольная работа. Роль протокольной работы в дипломатической деятельности
Протокольная работа. Роль протокольной работы в дипломатической деятельности Окончание процедуры банкротства и права кредиторов. (Лекция 6)
Окончание процедуры банкротства и права кредиторов. (Лекция 6) Национальное богатство
Национальное богатство  Методологические подходы в психологии
Методологические подходы в психологии органоиды1
органоиды1 Стеклообои
Стеклообои Методы обследования больных в клинике ортопедической стоматологии
Методы обследования больных в клинике ортопедической стоматологии Буферные системы
Буферные системы Внеклассное занятие к неделе географии
Внеклассное занятие к неделе географии Пересечение поверхностей
Пересечение поверхностей Защита персональных данных
Защита персональных данных Культурное пространство
Культурное пространство Применение дифракционного метода суммирования в геолокации
Применение дифракционного метода суммирования в геолокации