Содержание
- 2. Уравнение Шредингера Согласно постулату квантовой механики, состояние системы может быть описано определенной функцией координат, причем квадрат
- 3. Уравнение Шредингера Основная задача квантовой механики для стационарных состояний (частный случай спектральной задачи Штурма – Лиувилля
- 4. Собственно энергетическое представление Представление, в котором гамильтонова матрица диагональна, называется собственно энергетическим или собственным: Базис этого
- 5. Собственно энергетическое представление Собственные функции Ψ1 и Ψ2, отвечающие различным собственным значениям, ортогональны Если два оператора
- 6. Пример. Система из трех спинов Всего в системе будет 8 состояний, которые можно разбить на группы
- 7. Пример. Система из трех спинов Так как гамильтониан и оператор полного спина системы коммутируют, то гамильтонова
- 8. Инварианты матриц Процедура нахождения спектра сводится к преобразованию гамильтоновой матрицы к диагональному виду с помощью некоторого
- 9. Инварианты матриц Коэффициенты характеристического полинома являются инвариантами, в частности: След матрицы Определитель матрицы Важными инвариантами являются
- 11. Скачать презентацию








 Презентация Фискальная политика
Презентация Фискальная политика Ликвородинамика, оболочки, кровосн, аномалии
Ликвородинамика, оболочки, кровосн, аномалии  Всероссийский творческий фестиваль «Верим в село! Гордимся Россией!»
Всероссийский творческий фестиваль «Верим в село! Гордимся Россией!»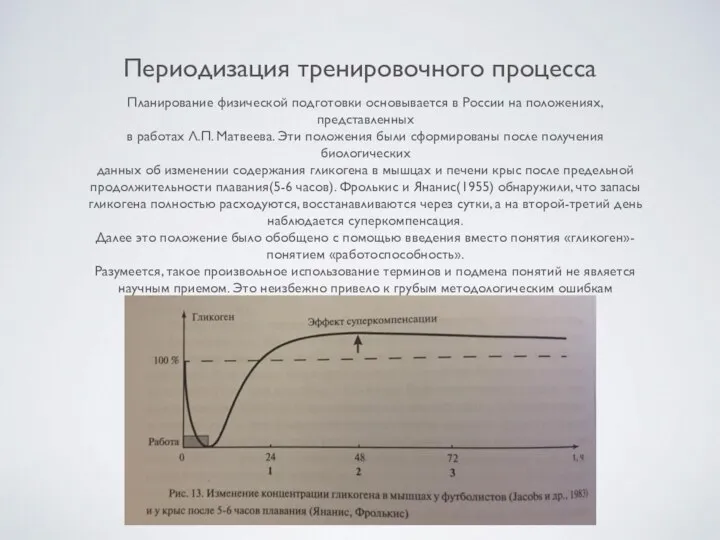 Периодизация тренировочного процесса
Периодизация тренировочного процесса Основы гематологии для инженеров. Приборы, реагенты, кровь
Основы гематологии для инженеров. Приборы, реагенты, кровь Презентация "Образ твой, над Русью вознесенный" - скачать презентации по МХК
Презентация "Образ твой, над Русью вознесенный" - скачать презентации по МХК Исследовательская программа Ф.А. фон Хайека. Лекция Н.А. Макашевой для 2-ого курса
Исследовательская программа Ф.А. фон Хайека. Лекция Н.А. Макашевой для 2-ого курса  Презентация "Опера. Самый значительный жанр вокальной музыки" - скачать презентации по МХК
Презентация "Опера. Самый значительный жанр вокальной музыки" - скачать презентации по МХК Стипендиальное обеспечение студентов
Стипендиальное обеспечение студентов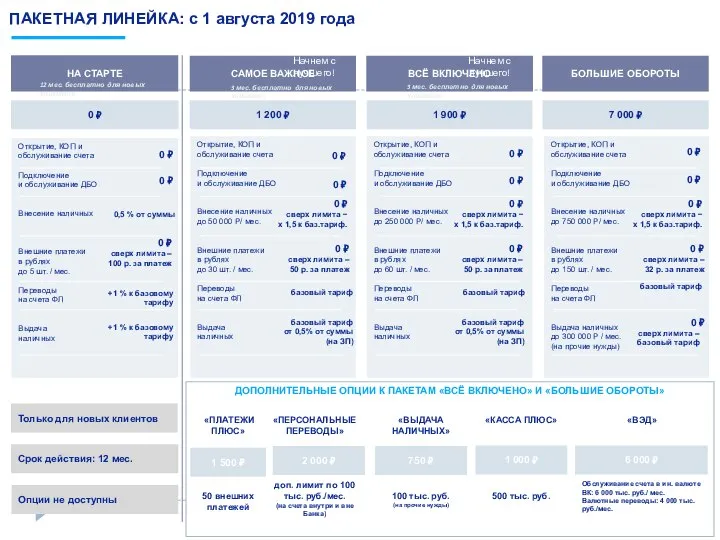 Пакетная линейка: c 1 августа 2019 года на старте
Пакетная линейка: c 1 августа 2019 года на старте Празднование Дней Европы в г. Одессе в 2018 году
Празднование Дней Европы в г. Одессе в 2018 году Словарное слово «ПОНЕДЕЛЬНИК
Словарное слово «ПОНЕДЕЛЬНИК  Обереги и талисманы
Обереги и талисманы История автомобилестроения
История автомобилестроения Litigation and enforcement in UK
Litigation and enforcement in UK Презентация Договор комиссии
Презентация Договор комиссии Исследование эффективности средств и методов подготовки легкоатлетов с учетом возраста и пола
Исследование эффективности средств и методов подготовки легкоатлетов с учетом возраста и пола 000189b6-519ac351
000189b6-519ac351 Первый ВТорой класс
Первый ВТорой класс наши подземные богатства - презентация для начальной школы
наши подземные богатства - презентация для начальной школы Презентация по МХК Театр в 18 веке в России
Презентация по МХК Театр в 18 веке в России Геохимия эндогенных процессов
Геохимия эндогенных процессов Цели внутреннего контроля и аудита финансового бизнес-цикла и его функции
Цели внутреннего контроля и аудита финансового бизнес-цикла и его функции Русские народные промыслы. Полхов-майданская роспись
Русские народные промыслы. Полхов-майданская роспись Ювелирное украшение башкирских девушек
Ювелирное украшение башкирских девушек Модели централизованного формирования норм поведения и подавления коррупции. МАСЭП 2015
Модели централизованного формирования норм поведения и подавления коррупции. МАСЭП 2015 Рак вульвы
Рак вульвы Лекція № 5 МАРКЕТИНГОВА ТОВАРНА ПОЛІТИКА
Лекція № 5 МАРКЕТИНГОВА ТОВАРНА ПОЛІТИКА