x
y
1
0
Масштаб π:3
−1
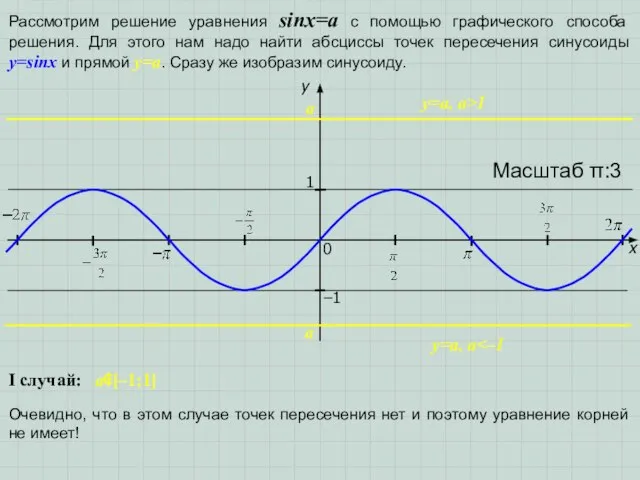
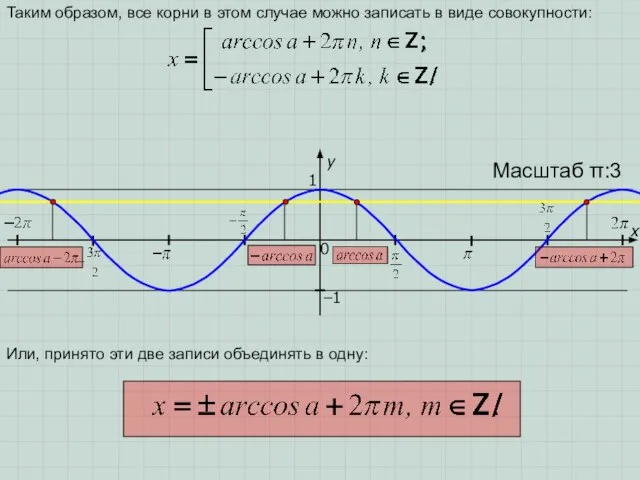
II случай: a∈[–1;1]
Очевидно, что в этом случае точек пересечения бесконечно
много, причем их абсциссы определяются следующим образом:
a
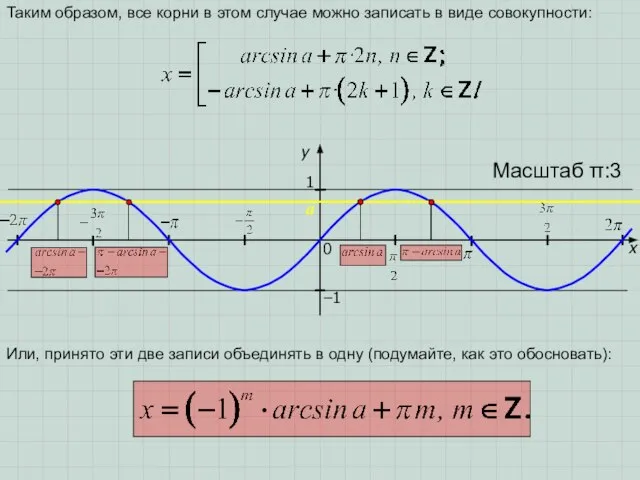
1) Рассмотрим точку, абсцисса которой попадает на отрезок .
2) Абсцисса этой точки – есть число(угол в радианной мере), синус которого равен a, т.е. значение этого числа равно arcsina.
3) Абсцисса второй точки, попадающей на отрезок [–π; π], равна (π–arcsina). Для объяснения этого достаточно вспомнить, что sinx=sin(π–x).
4) Все остальные абсциссы точек пересечения получаются из этих двух добавлением к ним чисел вида 2πn, где n∈ (ведь мы помним свойство периодичности функции y=sinx). Задание: назовите, какие абсциссы «улетевших» за край чертежа двух точек?
Ответ: (arcsina+2π) и (3π – arcsina).

![x y 1 0 Масштаб π:3 −1 II случай: a∈[–1;1] Очевидно,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1214030/slide-3.jpg)
![x y 1 0 Масштаб π:3 −1 II случай: a∈[–1;1] Очевидно,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1214030/slide-7.jpg)
 Механизм Отражения (Reflection) в C#
Механизм Отражения (Reflection) в C# Презентация на тему "Как правильно выбрать эффективный биологически активный препарат" - скачать презентации по Медицине
Презентация на тему "Как правильно выбрать эффективный биологически активный препарат" - скачать презентации по Медицине ТЕМА 5 БЕЗРАБОТИЦА В пользе безработицы больше всего уверены те, кто не знаком с ней по личному опыту. Джон Гелбрэйт, американски
ТЕМА 5 БЕЗРАБОТИЦА В пользе безработицы больше всего уверены те, кто не знаком с ней по личному опыту. Джон Гелбрэйт, американски Развития психики
Развития психики Рекурсия. Сортировка слиянием. Восходящая сортировка слиянием. Сложность сортировки. Устойчивость сортировок
Рекурсия. Сортировка слиянием. Восходящая сортировка слиянием. Сложность сортировки. Устойчивость сортировок Трансграничные туры социально-культурной направленности
Трансграничные туры социально-культурной направленности Нравственные основы службы в органах внутренних дел. Профессиональная этика сотрудника органов внутренних дел
Нравственные основы службы в органах внутренних дел. Профессиональная этика сотрудника органов внутренних дел Правовые основы охраны труда
Правовые основы охраны труда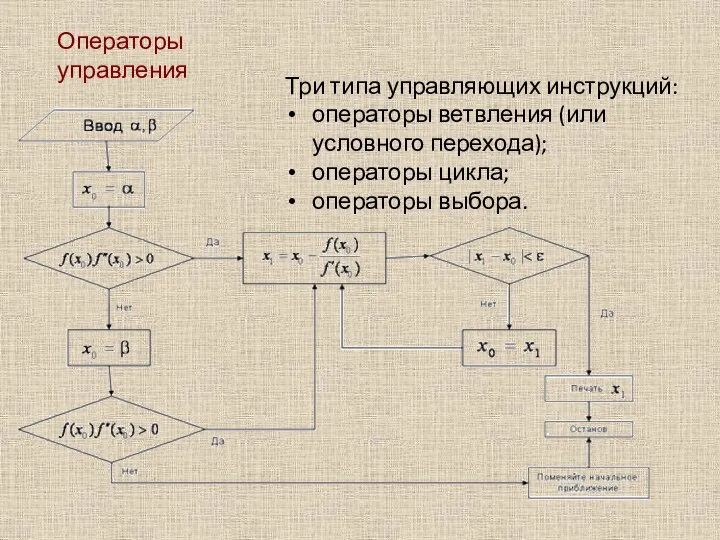 Операторы управления
Операторы управления Презентация Цена и общая стоимость контракта Виды цен Определение валюты цены
Презентация Цена и общая стоимость контракта Виды цен Определение валюты цены 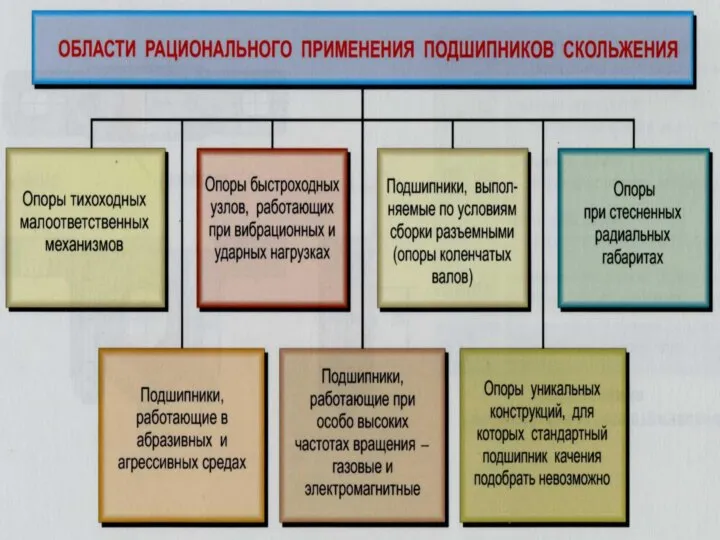 Области рационального применения подшипников скольжения
Области рационального применения подшипников скольжения Презентация Законы и иные источники ПСО. Их роль
Презентация Законы и иные источники ПСО. Их роль Litania Loretańska
Litania Loretańska Языки программирования
Языки программирования Методология научных исследований
Методология научных исследований Проблемно-контрольные вопросы Что такое институт права. Какие признаки присущи правовому институту? Что представляют собой
Проблемно-контрольные вопросы Что такое институт права. Какие признаки присущи правовому институту? Что представляют собой  НАЛОГОВЫЙ КОДЕКС: для транспортных предприятий
НАЛОГОВЫЙ КОДЕКС: для транспортных предприятий  Презентация Microsoft Office PowerPoint
Презентация Microsoft Office PowerPoint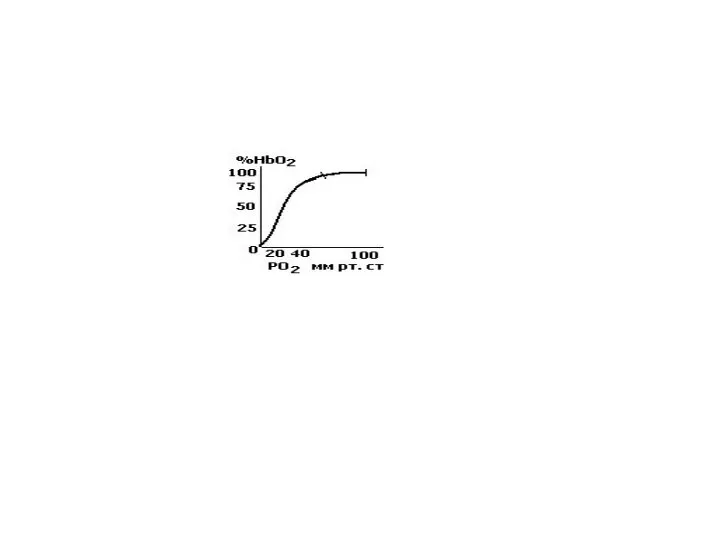 дыхание 2
дыхание 2 Устройство пк
Устройство пк  Аттестация как элемент планирования карьеры
Аттестация как элемент планирования карьеры Субиндексы степени развития бизнеса Нечаева Анастасия, Юрлова Виктория, МЭ-102
Субиндексы степени развития бизнеса Нечаева Анастасия, Юрлова Виктория, МЭ-102 Тензор поляризуемости диэлектрика
Тензор поляризуемости диэлектрика
 Регистры x86-64. Компьютерные основы программирования. Представление программ, часть 4
Регистры x86-64. Компьютерные основы программирования. Представление программ, часть 4 Инфляция «Инфляция — одна из форм налогообложения, не нуждающаяся в законодательном одобрении». Лауреат Нобелевской премии по
Инфляция «Инфляция — одна из форм налогообложения, не нуждающаяся в законодательном одобрении». Лауреат Нобелевской премии по Мужская парфюмерия
Мужская парфюмерия Политическая система
Политическая система Понятие и виды правомерного поведения
Понятие и виды правомерного поведения