Содержание
- 2. Для любых двух простейших чисел а и в выполняется одно из двух условий: либо а больше
- 3. Неравенства делятся на строгие и нестрогие Строгое неравенство А(х) > В(х) А(х) А(х) ≥ В(х) Строгое
- 4. Решим простейшее линейное неравенство ? 5х + 3 > 3х+7 Сначала вычтем из обеих частей 3х
- 5. Если х0 – решение данного неравенства, то, добавляя к обоим частям число с = - (3х0
- 6. Теперь решим квадратное неравенство ах2 + bх + с > 0, где а ≠ 0.
- 7. ? ! ? !
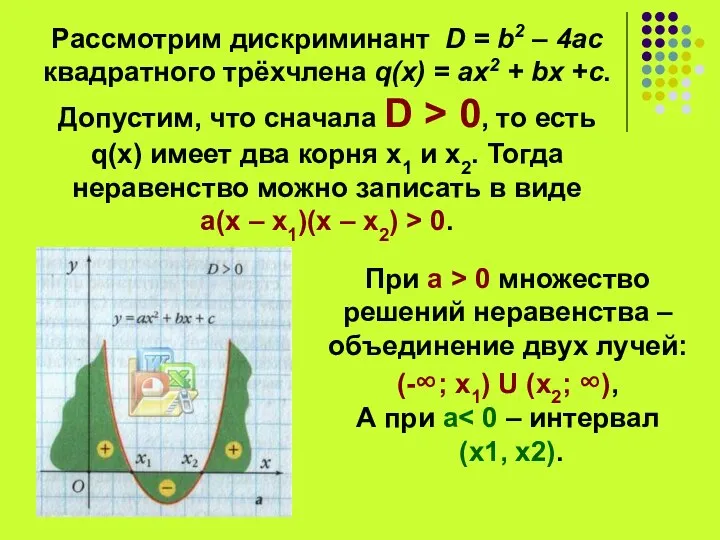
- 8. Рассмотрим дискриминант D = b2 – 4ac квадратного трёхчлена q(x) = aх2 + bx +c. Допустим,
- 9. Случай D = 0, когда х1 = х2 и q(x) = a(x –x1)2, рассматривается аналогично
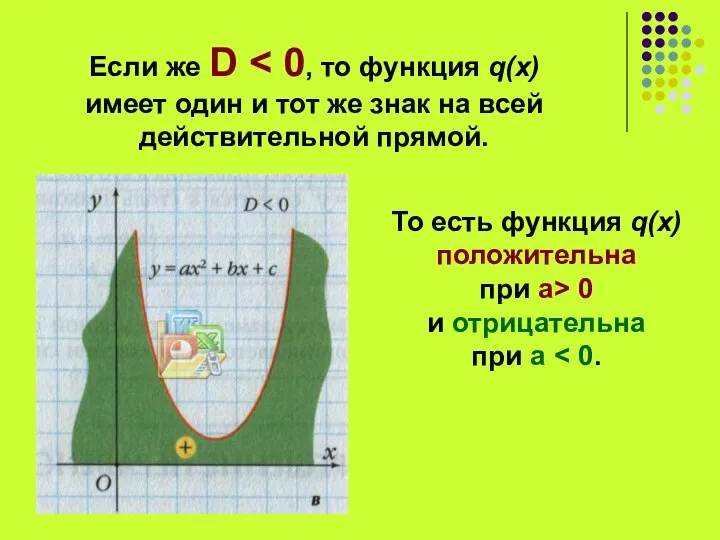
- 10. Если же D То есть функция q(x) положительна при а> 0 и отрицательна при а
- 11. Итог нашего маленького исследования подведём в следующей таблице:
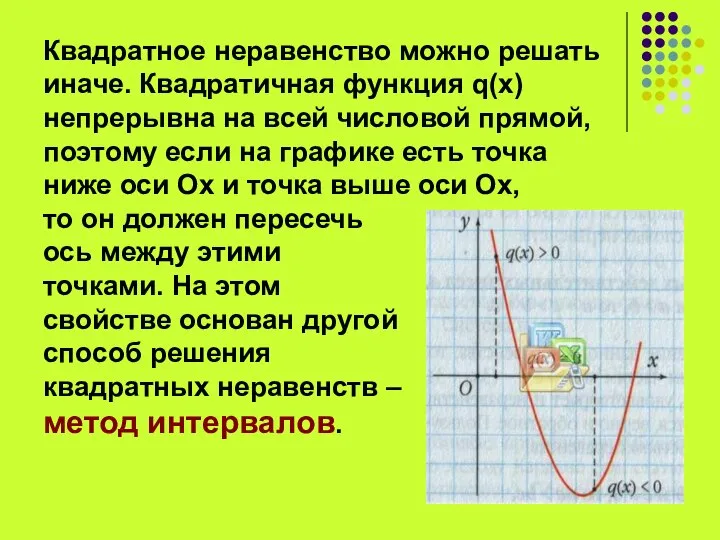
- 12. Квадратное неравенство можно решать иначе. Квадратичная функция q(x) непрерывна на всей числовой прямой, поэтому если на
- 13. Алгоритм решения неравенств методом интервалов (квадратных и не только): Найдём нули функции (абсциссы точек пересечения графика
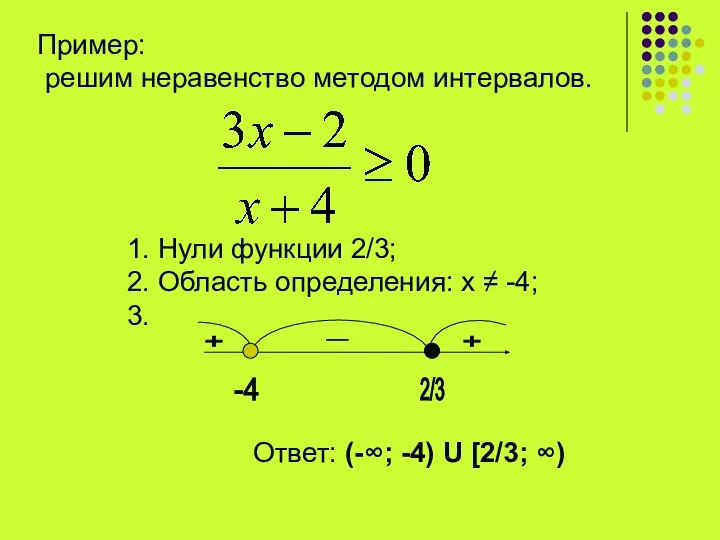
- 14. Пример: решим неравенство методом интервалов. 1. Нули функции 2/3; 2. Область определения: х ≠ -4; 3.
- 16. Скачать презентацию









 Анализ современного урока В помощь учителю
Анализ современного урока В помощь учителю Художественная культура XIX столетия
Художественная культура XIX столетия Развитие государственных муниципальных закупок в системе управления экономикой страны
Развитие государственных муниципальных закупок в системе управления экономикой страны Статистика труда
Статистика труда  Технические каналы утечки информации на объектах информатизации Вооруженных Сил
Технические каналы утечки информации на объектах информатизации Вооруженных Сил Проектирование СТО автомобилей, с разработкой поста технического обслуживания и моделированием детали автомобиля
Проектирование СТО автомобилей, с разработкой поста технического обслуживания и моделированием детали автомобиля Системный подход к содержанию культуры
Системный подход к содержанию культуры Теория разработки рекламных объявлений
Теория разработки рекламных объявлений Презентация Поправка к цене контракта. Виды скидок во внешнеторговом контракте
Презентация Поправка к цене контракта. Виды скидок во внешнеторговом контракте  Богородице-Рождественский женский монастырь. Воскресная школа «Лучик»
Богородице-Рождественский женский монастырь. Воскресная школа «Лучик» «Молодёжные субкультуры»
«Молодёжные субкультуры» Экспортный контроль в системе управления ВЭД
Экспортный контроль в системе управления ВЭД Принтеры
Принтеры Биосфера с пз
Биосфера с пз Презентация Уравнения с параметрами
Презентация Уравнения с параметрами Презентация на тему "Анатомия и физиология как науки. Понятие об органе и системах органов. Организм в целом" - скачать презент
Презентация на тему "Анатомия и физиология как науки. Понятие об органе и системах органов. Организм в целом" - скачать презент Экспедиция «Мориа - 2018» КЧР
Экспедиция «Мориа - 2018» КЧР Основы программирования - Java ФИСТ 1 курс
Основы программирования - Java ФИСТ 1 курс Вимоги до диякона
Вимоги до диякона Государство 2
Государство 2 Разработка виртуального тренажера процесса пастеризации в среде Labview
Разработка виртуального тренажера процесса пастеризации в среде Labview Мать Тереза
Мать Тереза Коммуникация и общество
Коммуникация и общество Мясо Мангал. Игра, Миссия или Бизнес?
Мясо Мангал. Игра, Миссия или Бизнес? Конституционно-правовые основы правотворческих полномочий и виды подзаконных правовых актов органов государственной власти РФ
Конституционно-правовые основы правотворческих полномочий и виды подзаконных правовых актов органов государственной власти РФ Контроллер. Проектирование и разработка веб-сервисов
Контроллер. Проектирование и разработка веб-сервисов скелет
скелет Связь явлений Часть 2
Связь явлений Часть 2