Содержание
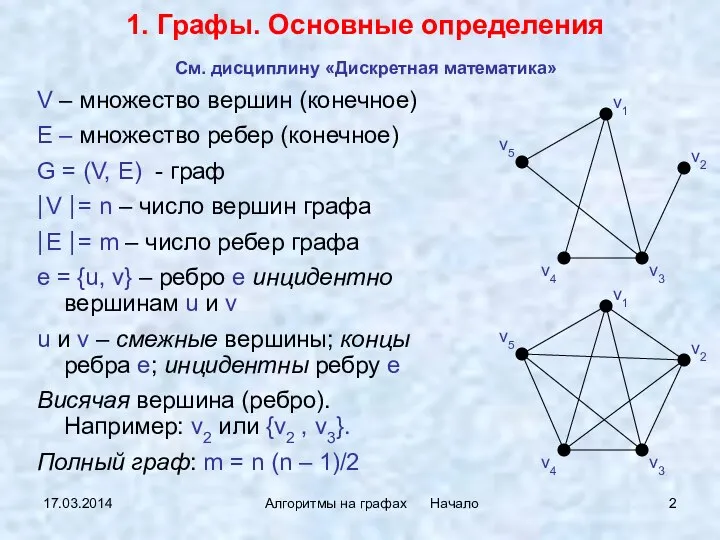
- 2. 17.03.2014 Алгоритмы на графах Начало 1. Графы. Основные определения V – множество вершин (конечное) E –
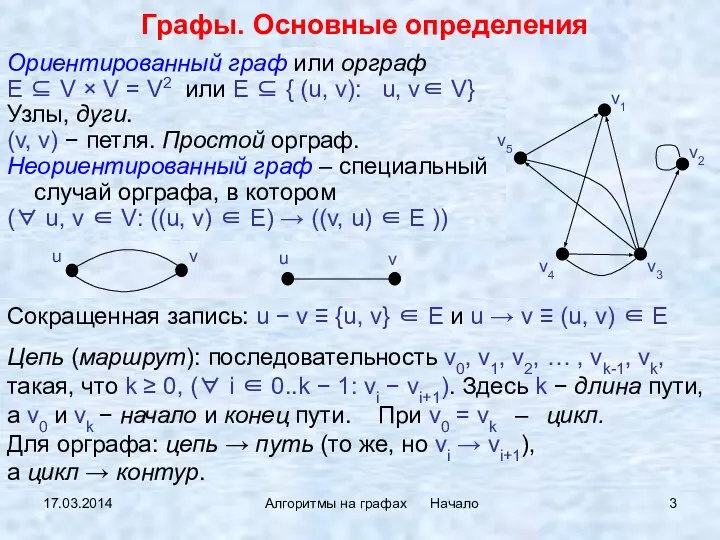
- 3. 17.03.2014 Алгоритмы на графах Начало Ориентированный граф или орграф E ⊆ V × V = V2
- 4. 17.03.2014 Алгоритмы на графах Начало Графы. Основные определения Аналогично для графа (неориентированного графа) E ⊆ {
- 5. 17.03.2014 Алгоритмы на графах Начало Степень вершины d(v) – число инцидентных ей ребер (дуг). Для орграфа:
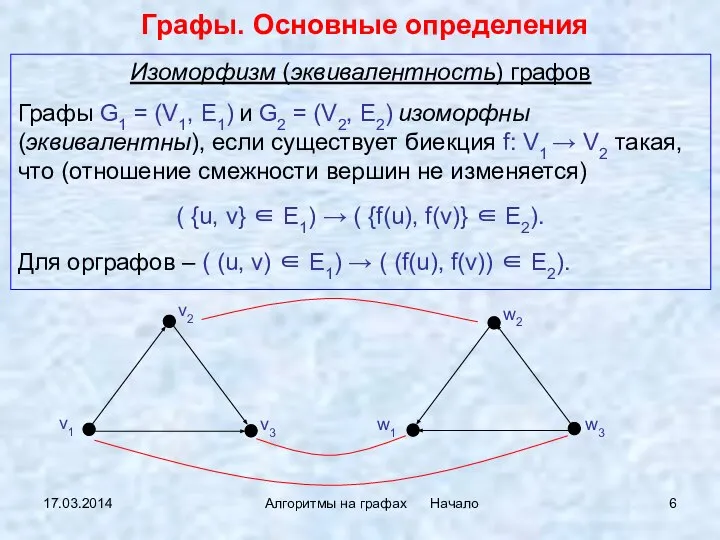
- 6. 17.03.2014 Алгоритмы на графах Начало Графы. Основные определения Изоморфизм (эквивалентность) графов Графы G1 = (V1, E1)
- 7. 17.03.2014 Алгоритмы на графах Начало Другое определение графа (орграфа) Отступление. Соответствие Графы и бинарные отношения. Бинарное
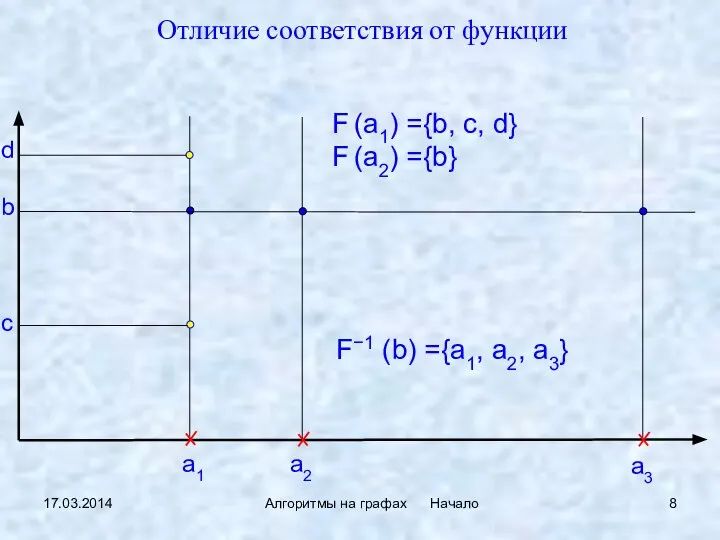
- 8. 17.03.2014 Алгоритмы на графах Начало b a1 F−1 (b) ={a1, a2, a3} a2 a3 F (a1)
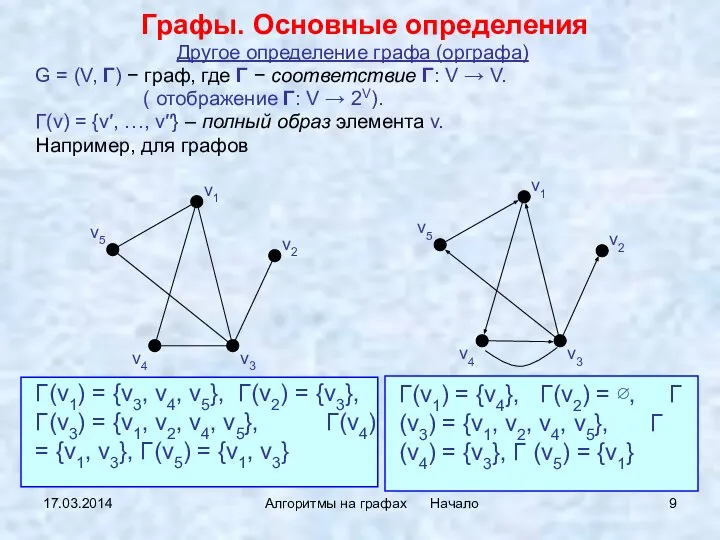
- 9. 17.03.2014 Алгоритмы на графах Начало Другое определение графа (орграфа) G = (V, Γ) − граф, где
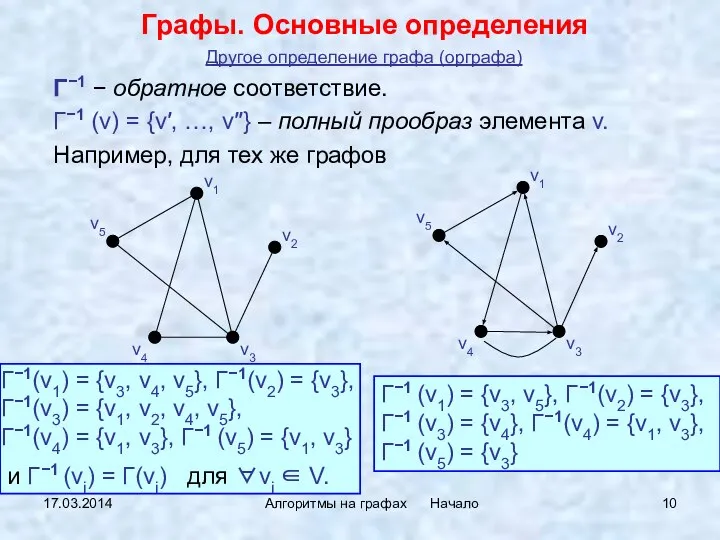
- 10. 17.03.2014 Алгоритмы на графах Начало Γ−1 − обратное соответствие. Γ−1 (v) = {v′, …, v′′} –
- 11. 17.03.2014 Алгоритмы на графах Начало Упорядоченный граф G = (V, L) − упорядоченный граф, где L
- 12. 17.03.2014 Алгоритмы на графах Начало Упорядоченный граф Упорядоченные графы G1 = (V1, L 1) и G2
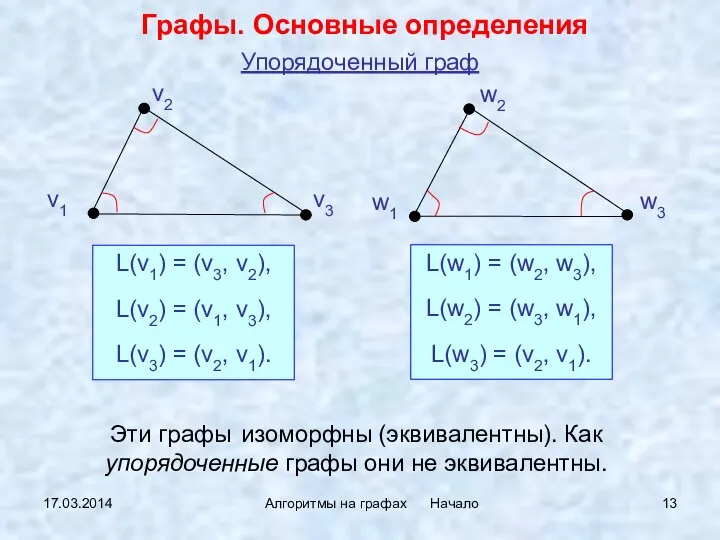
- 13. 17.03.2014 Алгоритмы на графах Начало Упорядоченный граф Графы. Основные определения v1 v2 v3 w1 w2 w3
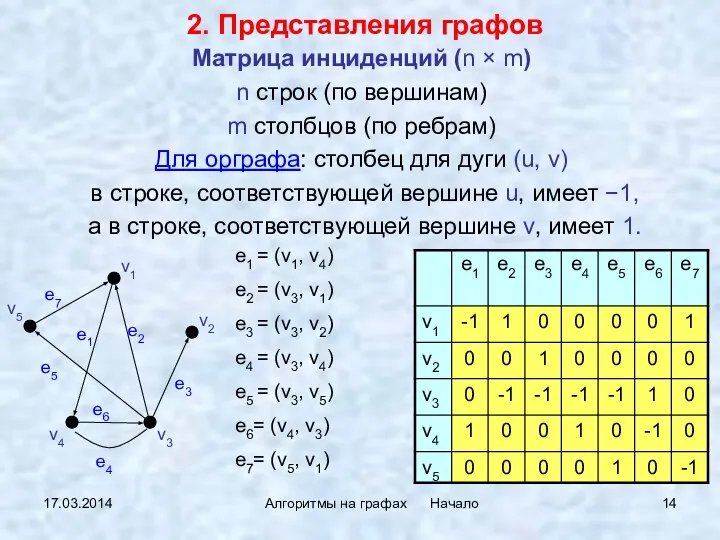
- 14. 17.03.2014 Алгоритмы на графах Начало Матрица инциденций (n × m) n строк (по вершинам) m столбцов
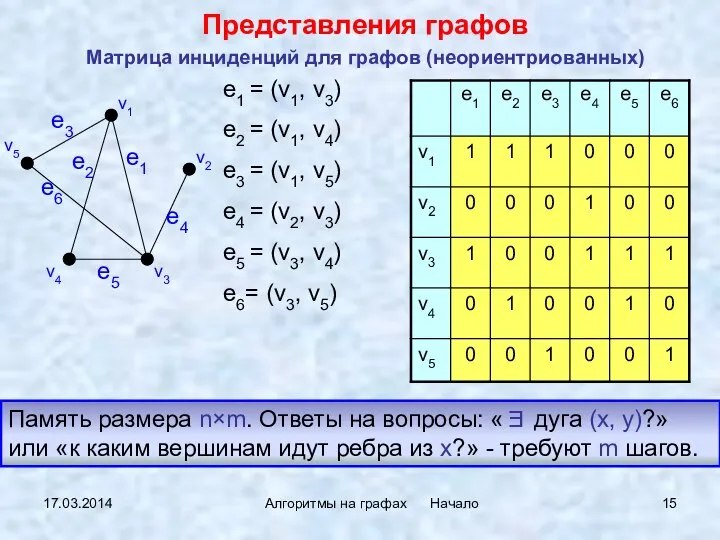
- 15. 17.03.2014 Алгоритмы на графах Начало Матрица инциденций для графов (неориентриованных) Представления графов e1 = (v1, v3)
- 16. 17.03.2014 Алгоритмы на графах Начало A[u, v] = 1, если u − v или u →
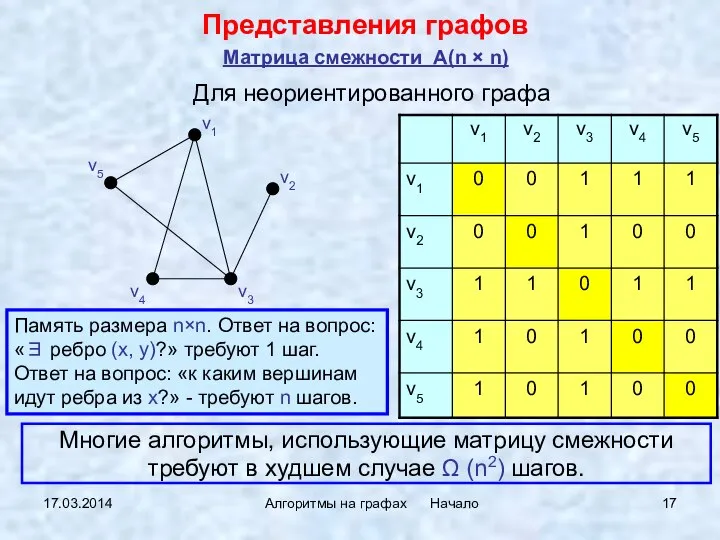
- 17. 17.03.2014 Алгоритмы на графах Начало Для неориентированного графа Представления графов Матрица смежности A(n × n) Память
- 18. 17.03.2014 Алгоритмы на графах Начало Списки смежности Adj[1..n] – массив списков (adjacent – смежный, соседний) Adj[v]
- 19. 17.03.2014 Алгоритмы на графах Начало Списки смежности Реализация упорядоченного графа Adj[1..n] – массив списков (adjacent –
- 20. 17.03.2014 Алгоритмы на графах Начало Списки смежности for ∀u∈ Adj [v] do S(u) ≡ begin L
- 21. 17.03.2014 Алгоритмы на графах Начало Задание: Написать код преобразования одного представления графа (орграфа) в другое. Виды
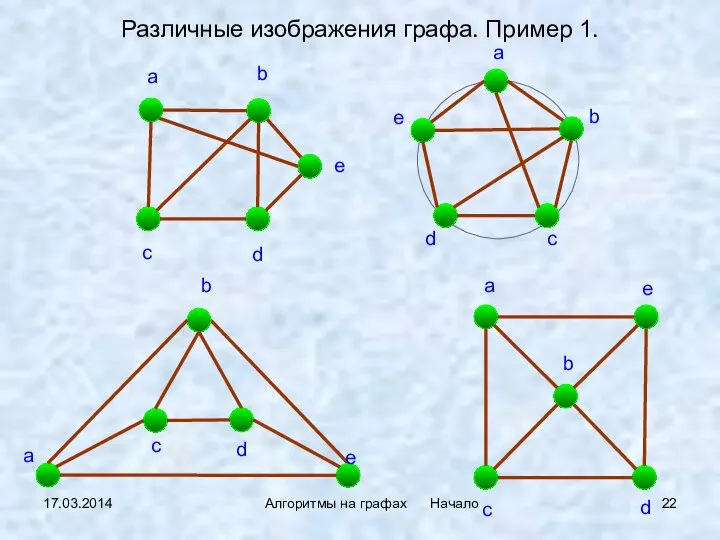
- 22. 17.03.2014 Алгоритмы на графах Начало Различные изображения графа. Пример 1.
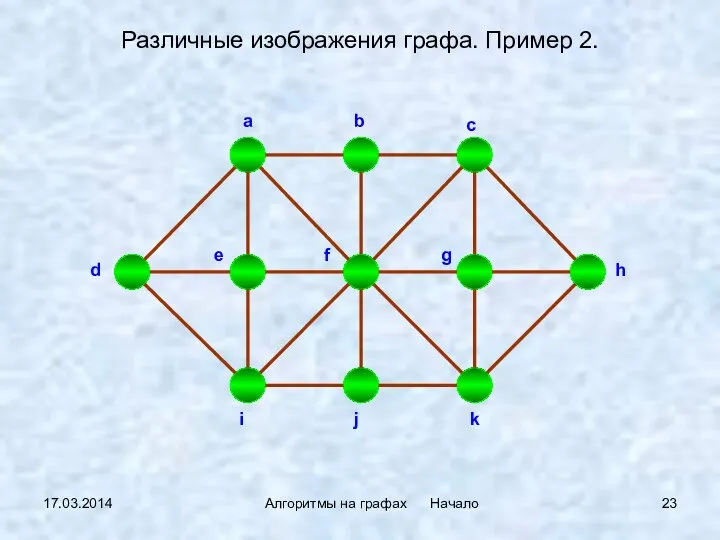
- 23. 17.03.2014 Алгоритмы на графах Начало Различные изображения графа. Пример 2.
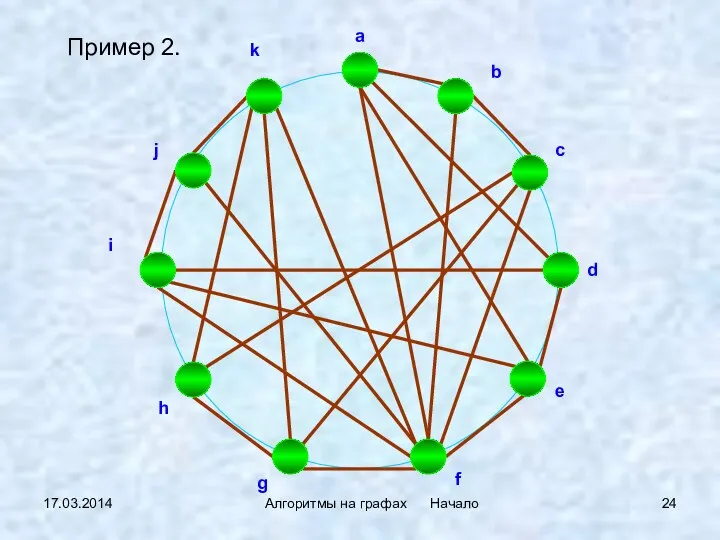
- 24. 17.03.2014 Алгоритмы на графах Начало Пример 2.
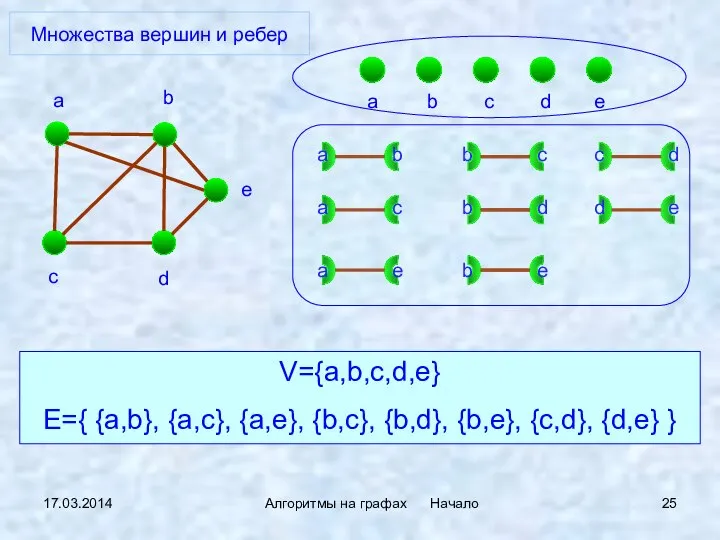
- 25. 17.03.2014 Алгоритмы на графах Начало Множества вершин и ребер V={a,b,c,d,e} E={ {a,b}, {a,c}, {a,e}, {b,c}, {b,d},
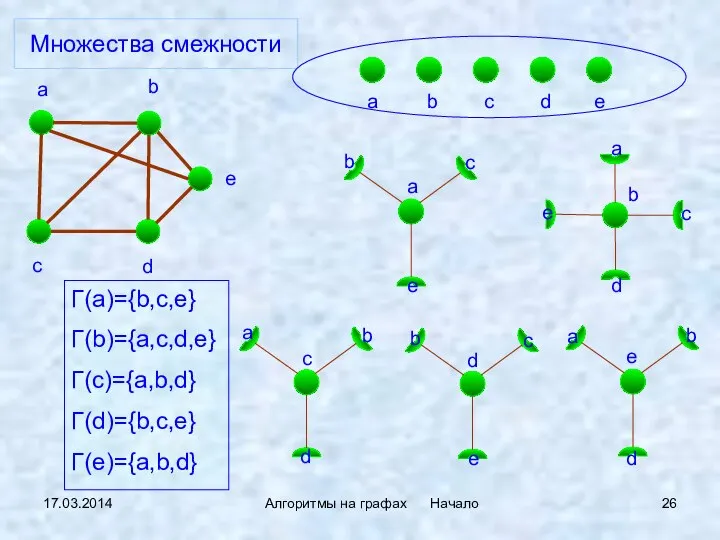
- 26. 17.03.2014 Алгоритмы на графах Начало Множества смежности Γ(a)={b,c,e} Γ(b)={a,c,d,e} Γ(c)={a,b,d} Γ(d)={b,c,e} Γ(e)={a,b,d}
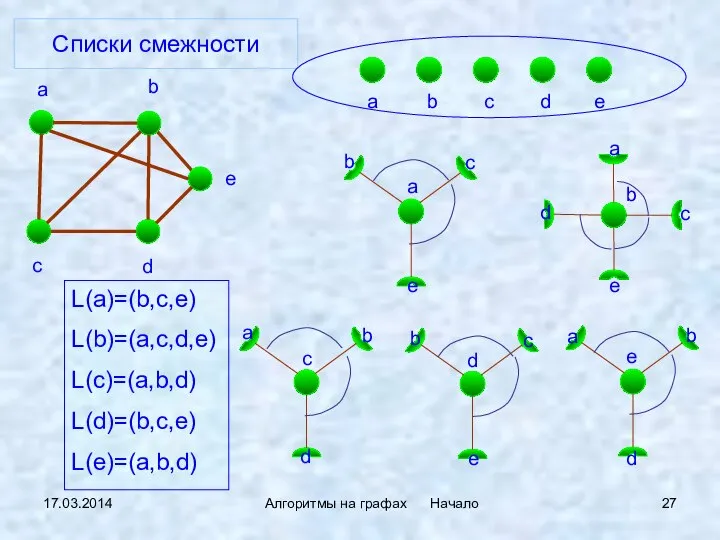
- 27. 17.03.2014 Алгоритмы на графах Начало Списки смежности L(a)=(b,c,e) L(b)=(a,c,d,e) L(c)=(a,b,d) L(d)=(b,c,e) L(e)=(a,b,d)
- 28. 17.03.2014 Алгоритмы на графах Начало Конец вводной части
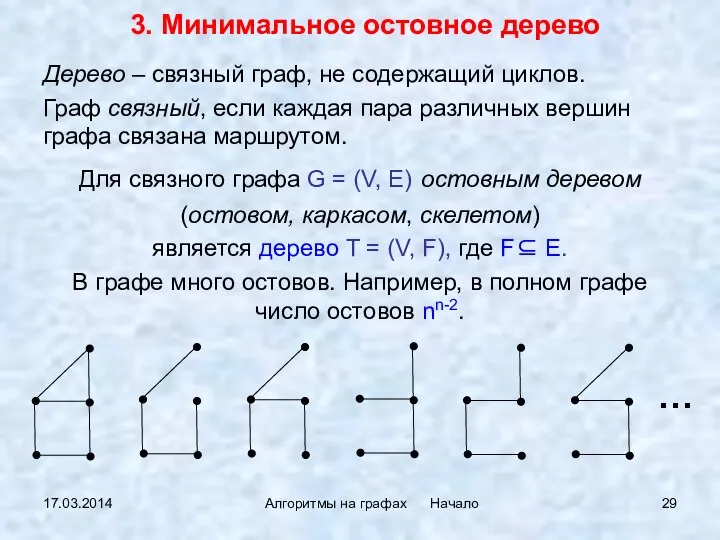
- 29. 17.03.2014 Алгоритмы на графах Начало Дерево – связный граф, не содержащий циклов. Граф связный, если каждая
- 30. 17.03.2014 Алгоритмы на графах Начало Остовные деревья (леса) Пример. Задача «связности» (Седжвик). Задан граф. Пусть номера
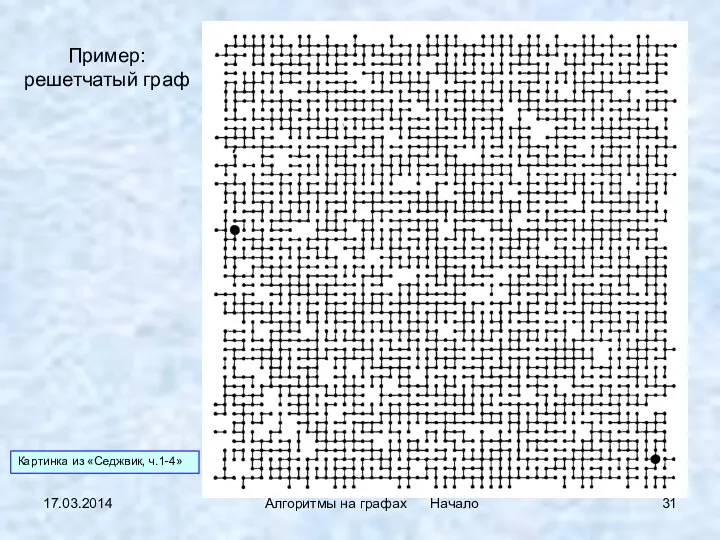
- 31. 17.03.2014 Алгоритмы на графах Начало Пример: решетчатый граф Картинка из «Седжвик, ч.1-4»
- 32. 17.03.2014 Алгоритмы на графах Начало Рассмотрим простой вариант задачи связности Предъявляется последовательность ребер графа: i1 –
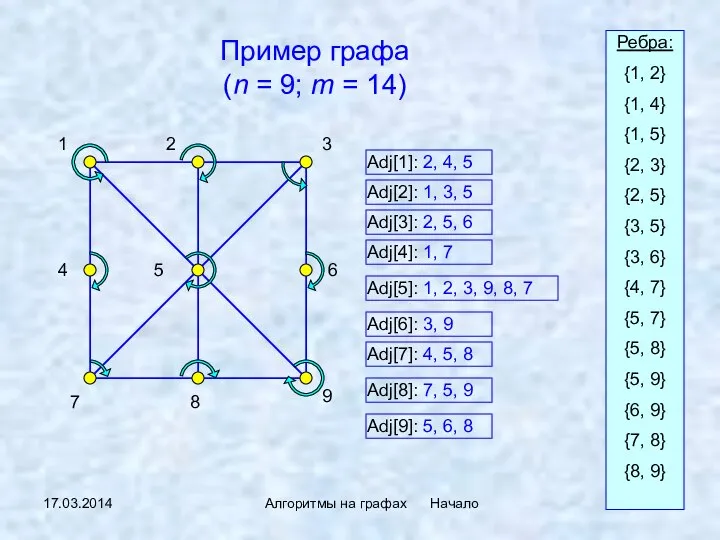
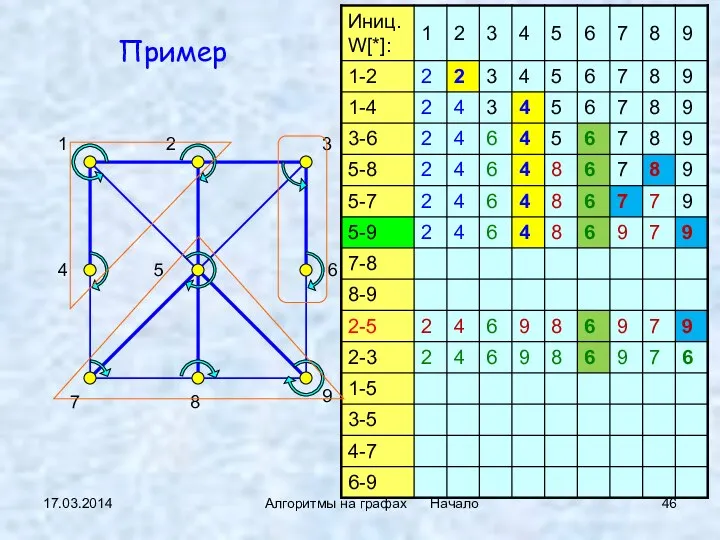
- 33. 17.03.2014 Алгоритмы на графах Начало Пример графа (n = 9; m = 14) Adj[1]: 2, 4,
- 34. 17.03.2014 Алгоритмы на графах Начало Пример Идея: пусть на некотором шаге сформирован остовный лес (выделены подмножества
- 35. 17.03.2014 Алгоритмы на графах Начало Алгоритм for (i = 1; i // Все деревья – изолированные
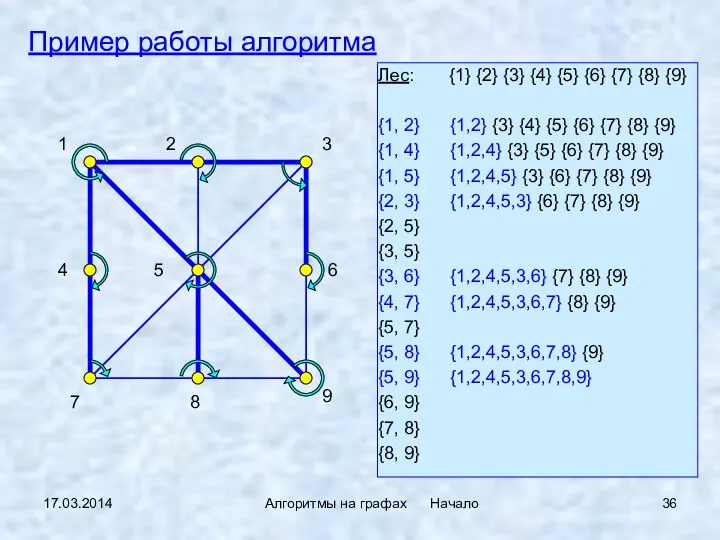
- 36. 17.03.2014 Алгоритмы на графах Начало Пример работы алгоритма Лес: {1} {2} {3} {4} {5} {6} {7}
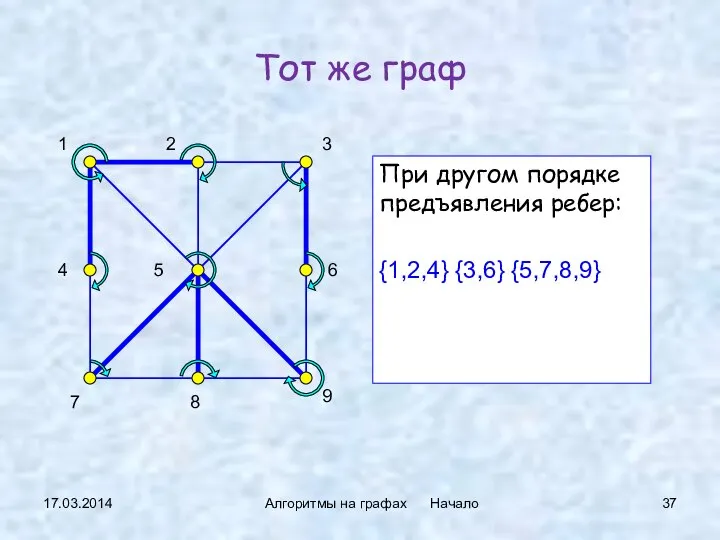
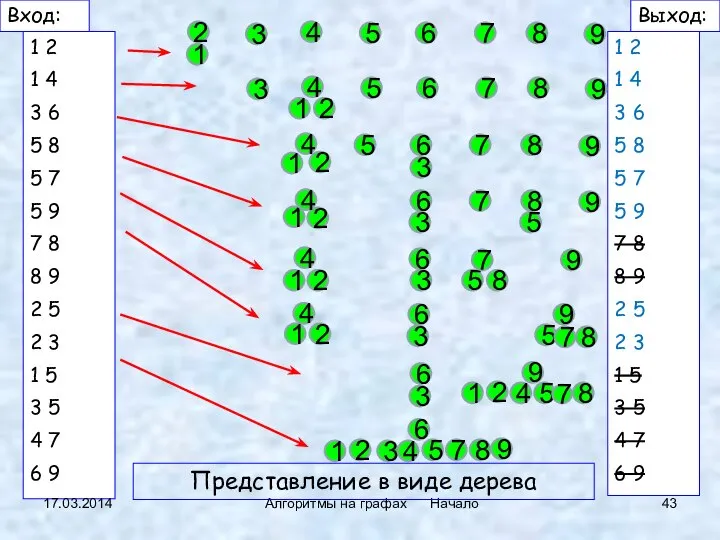
- 37. 17.03.2014 Алгоритмы на графах Начало Тот же граф При другом порядке предъявления ребер: {1,2,4} {3,6} {5,7,8,9}
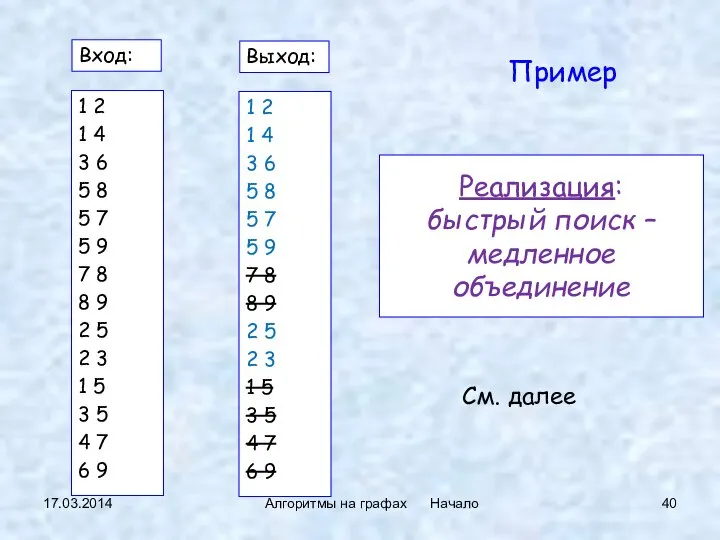
- 38. 17.03.2014 Алгоритмы на графах Начало Реализация: быстрый поиск – медленное объединение for (i = 1; i
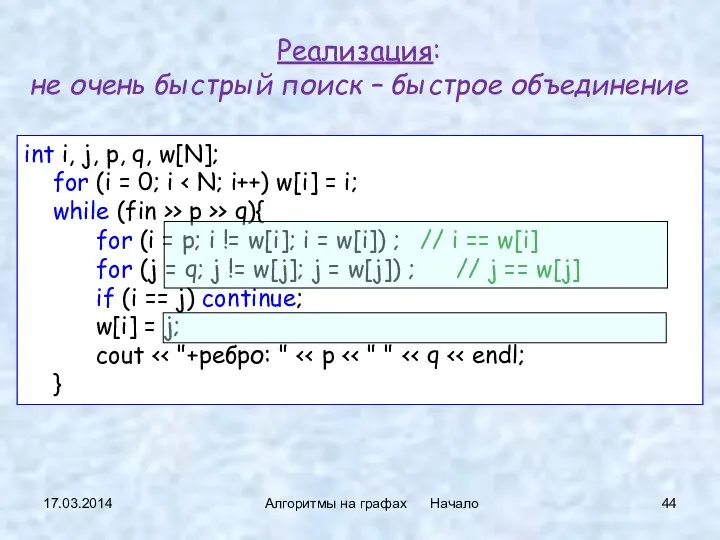
- 39. int i, j, k, p, q, w[N]; for (i = 0; i while (fin >> p
- 40. 1 2 1 4 3 6 5 8 5 7 5 9 7 8 8 9
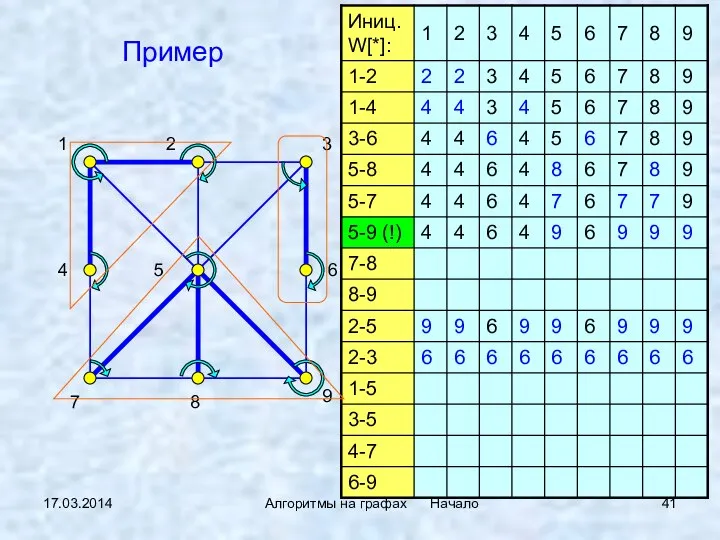
- 41. 17.03.2014 Алгоритмы на графах Начало Пример
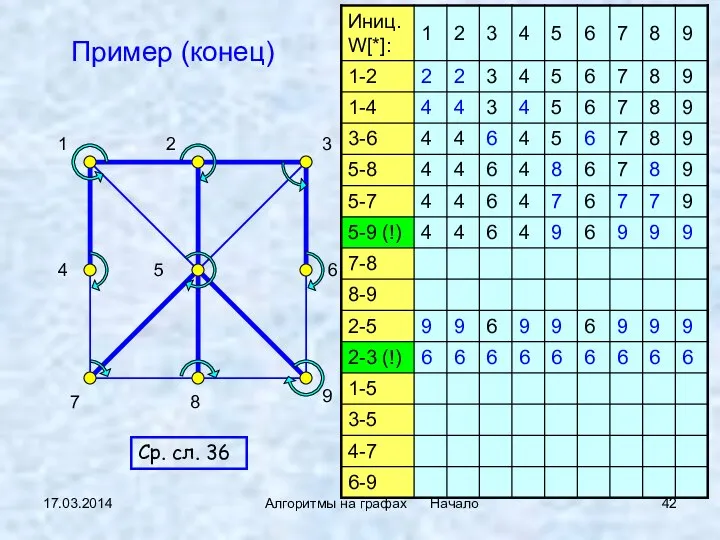
- 42. 17.03.2014 Алгоритмы на графах Начало Пример (конец) Ср. сл. 36
- 43. 1 2 1 4 3 6 5 8 5 7 5 9 7 8 8 9
- 44. Реализация: не очень быстрый поиск – быстрое объединение 17.03.2014 Алгоритмы на графах Начало int i, j,
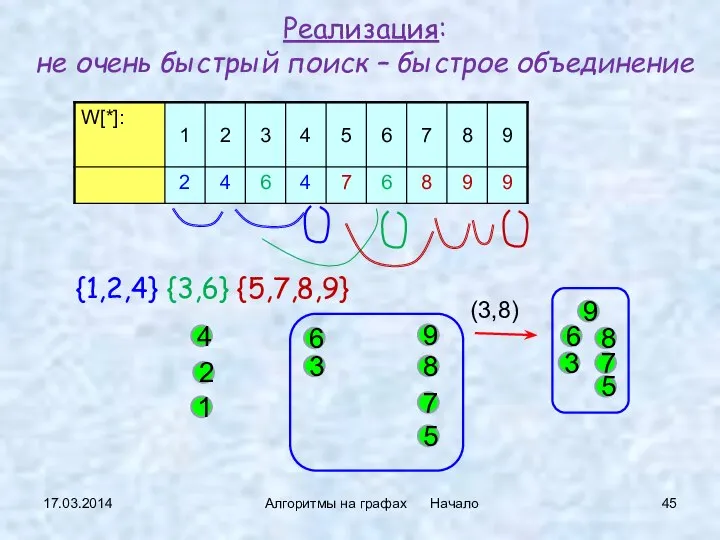
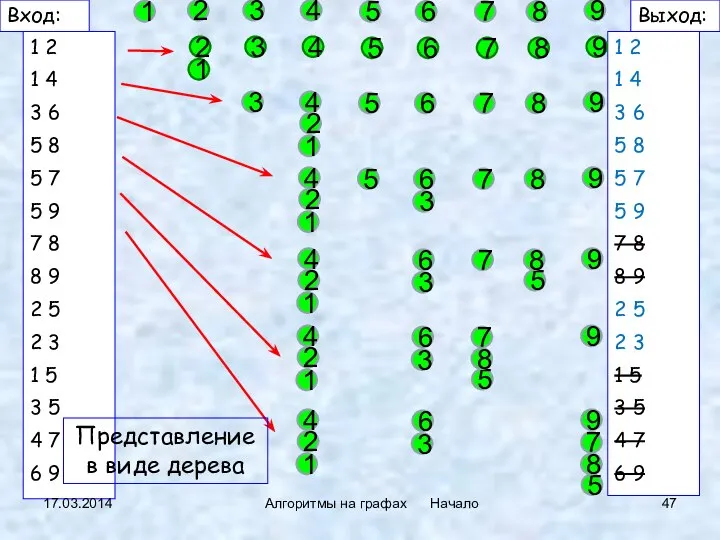
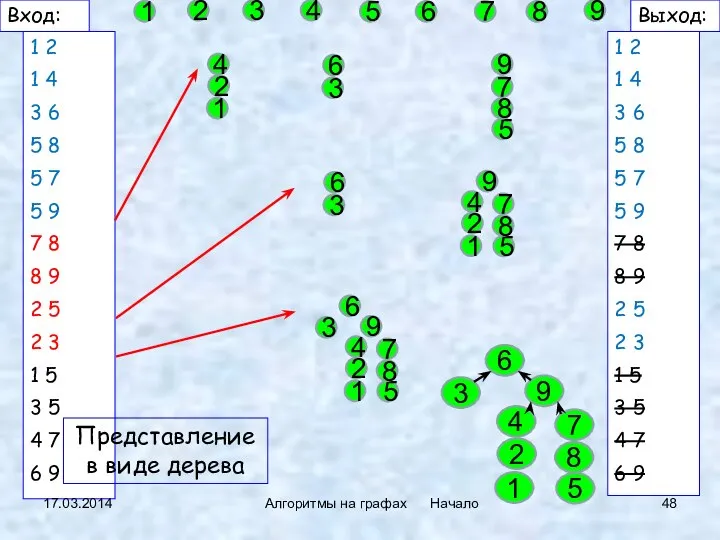
- 45. 17.03.2014 Алгоритмы на графах Начало {1,2,4} {3,6} {5,7,8,9} Реализация: не очень быстрый поиск – быстрое объединение
- 46. 17.03.2014 Алгоритмы на графах Начало Пример
- 47. 1 2 1 4 3 6 5 8 5 7 5 9 7 8 8 9
- 48. 1 2 1 4 3 6 5 8 5 7 5 9 7 8 8 9
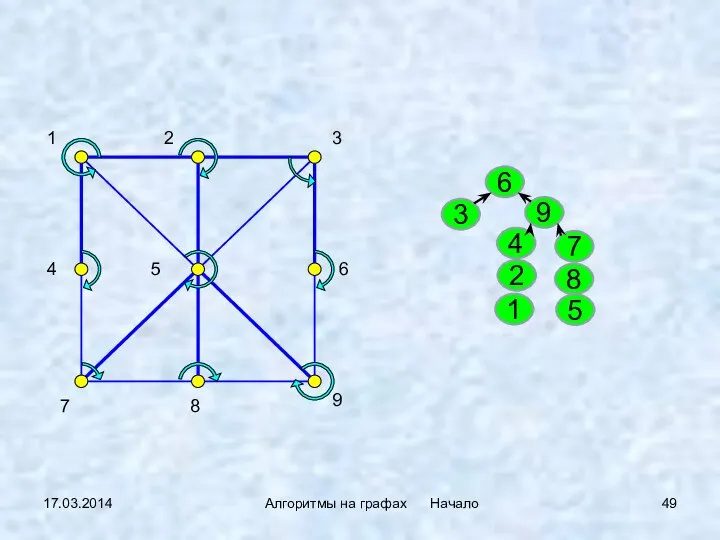
- 49. 17.03.2014 Алгоритмы на графах Начало
- 50. 17.03.2014 Алгоритмы на графах Начало Граф G = (V, E). Матрица весов W[v, u]. Пусть T
- 51. 17.03.2014 Алгоритмы на графах Начало Продолжение задачи «Построение МОД» на следующей лекции
- 53. Скачать презентацию





![17.03.2014 Алгоритмы на графах Начало A[u, v] = 1, если u](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301909/slide-15.jpg)
![17.03.2014 Алгоритмы на графах Начало Списки смежности Adj[1..n] – массив списков](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301909/slide-17.jpg)
![17.03.2014 Алгоритмы на графах Начало Списки смежности Реализация упорядоченного графа Adj[1..n]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301909/slide-18.jpg)
![17.03.2014 Алгоритмы на графах Начало Списки смежности for ∀u∈ Adj [v]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301909/slide-19.jpg)







![int i, j, k, p, q, w[N]; for (i = 0;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1301909/slide-38.jpg)


 Психологические и медико-биологические проблемы физической культуры и спорта
Психологические и медико-биологические проблемы физической культуры и спорта Социальная антропология Республики Кореи
Социальная антропология Республики Кореи Презентация на тему "Дымова И.Е" - скачать презентации по Педагогике
Презентация на тему "Дымова И.Е" - скачать презентации по Педагогике ФОРМИРОВАНИЕ СИСТЕМЫ АДАПТАЦИИ ПЕРСОНАЛА НА ПРЕДПРИЯТИИ Выполнила студентка Н.В.Александрова гр.О-3272
ФОРМИРОВАНИЕ СИСТЕМЫ АДАПТАЦИИ ПЕРСОНАЛА НА ПРЕДПРИЯТИИ Выполнила студентка Н.В.Александрова гр.О-3272 15 лет шахматному клубу «Вертикаль» г. Сатка
15 лет шахматному клубу «Вертикаль» г. Сатка Управление освещением. Программирование в ONI PLR studio
Управление освещением. Программирование в ONI PLR studio Проблемы ограничения свободы СМИ
Проблемы ограничения свободы СМИ Интегрированный урок географии, естествознания
Интегрированный урок географии, естествознания Учебный предмет черчение. История развития чертежа
Учебный предмет черчение. История развития чертежа Понятие и признаки гражданского правоотношения
Понятие и признаки гражданского правоотношения Использование динамической памяти при организации списков и их обработке. Лекция 10
Использование динамической памяти при организации списков и их обработке. Лекция 10 Федеральная Антимонопольная Служба: чем она занимается и чем полезна потребителю
Федеральная Антимонопольная Служба: чем она занимается и чем полезна потребителю Основи будови військових засобів вимірювань. Засоби вимірювань
Основи будови військових засобів вимірювань. Засоби вимірювань Презентация Future of Ukraine
Презентация Future of Ukraine Устройства ввода и вывода информации
Устройства ввода и вывода информации Презентация Педагогическое взаимодействие
Презентация Педагогическое взаимодействие Українська мова
Українська мова Презентация к уроку «Наш край» Куликов Иван Семенович Подготовила: А.А.Лукьянова 2011 год
Презентация к уроку «Наш край» Куликов Иван Семенович Подготовила: А.А.Лукьянова 2011 год  Наркотические вещества, классификация, влияние на организм, профилактика
Наркотические вещества, классификация, влияние на организм, профилактика Презентация ВАЖНЕЙШИЕ ФАКТОРЫ РАЗВИТИЯ УПРАВЛЕНЧЕСКОЙ МЫСЛИ В РОССИИ XVII в
Презентация ВАЖНЕЙШИЕ ФАКТОРЫ РАЗВИТИЯ УПРАВЛЕНЧЕСКОЙ МЫСЛИ В РОССИИ XVII в Основы химического производства пластмасс
Основы химического производства пластмасс Коллективный договор как фактор мотивации профсоюзного членства
Коллективный договор как фактор мотивации профсоюзного членства Классицизм (от латинского- «образцовый»)
Классицизм (от латинского- «образцовый») Колобок
Колобок  Ау! Волонтеры! или как справиться с «кризисом доверия» 28 октября 2011, институт журналистики и массовой коммуникации КПУ, Альберт
Ау! Волонтеры! или как справиться с «кризисом доверия» 28 октября 2011, институт журналистики и массовой коммуникации КПУ, Альберт  Презентация Оценка результативности поведения персонала
Презентация Оценка результативности поведения персонала Помоги Митюше сделать хохломскую ложку. Игра
Помоги Митюше сделать хохломскую ложку. Игра Сканирование карт
Сканирование карт