Содержание
- 2. Целочисленные алгоритмы (язык Си) Тема 1. Алгоритм Евклида © К.Ю. Поляков, 2008-2009
- 3. Вычисление НОД НОД = наибольший общий делитель двух натуральных чисел – это наибольшее число, на которое
- 4. Алгоритм Евклида Евклид (365-300 до. н. э.) НОД(a,b)= НОД(a-b, b) = НОД(a, b-a) Заменяем большее из
- 5. Модифицированный алгоритм Евклида НОД(a,b)= НОД(a%b, b) = НОД(a, b%a) Заменяем большее из двух чисел остатком от
- 6. Реализация алгоритма Евклида Рекурсивный вариант: Без рекурсии: int NOD ( int a, int b ) {
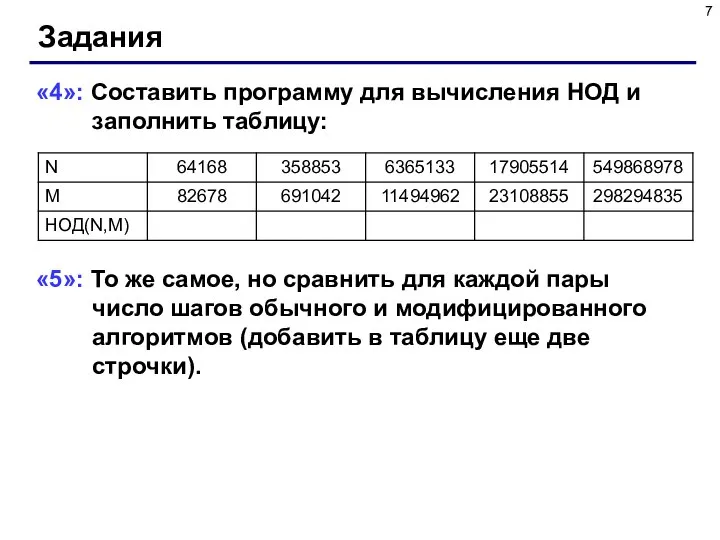
- 7. Задания «4»: Составить программу для вычисления НОД и заполнить таблицу: «5»: То же самое, но сравнить
- 8. Целочисленные алгоритмы (язык Си) Тема 2. Решето Эратосфена © К.Ю. Поляков, 2008-2009
- 9. Поиск простых чисел Простые числа – это числа, которые делятся только на себя и на 1.
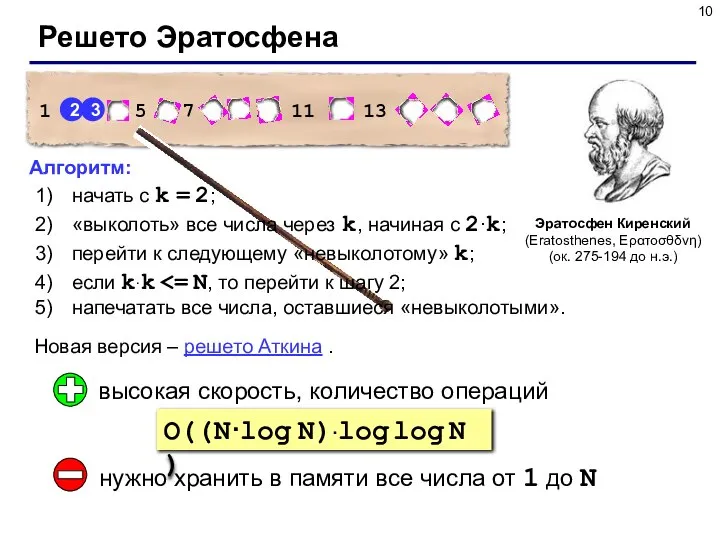
- 10. Решето Эратосфена Эратосфен Киренский (Eratosthenes, Ερατοσθδνη) (ок. 275-194 до н.э.) Новая версия – решето Аткина .
- 11. Реализация // сначала все числа не выколоты for ( i = 1; i A[i] = 1;
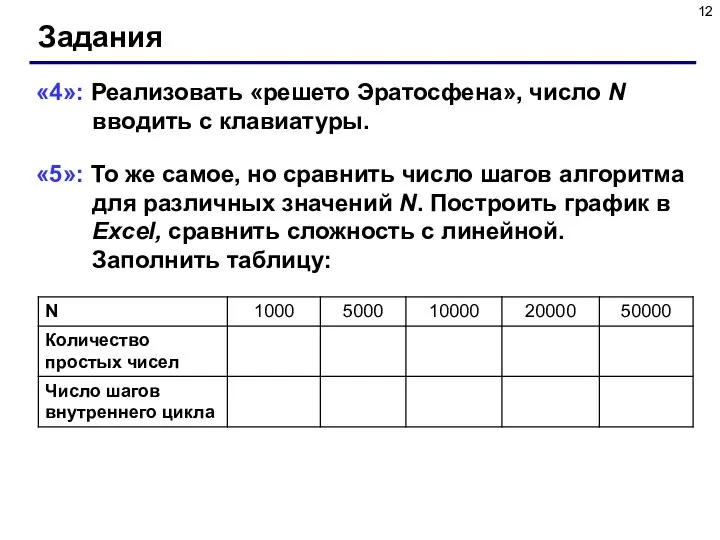
- 12. Задания «4»: Реализовать «решето Эратосфена», число N вводить с клавиатуры. «5»: То же самое, но сравнить
- 13. Целочисленные алгоритмы (язык Си) Тема 3. Длинные числа © К.Ю. Поляков, 2008-2009
- 14. Что такое длинные числа? Задача. Вычислить (точно) 100! = 1·2·3·...·99·100 Проблема: это число содержит более 100
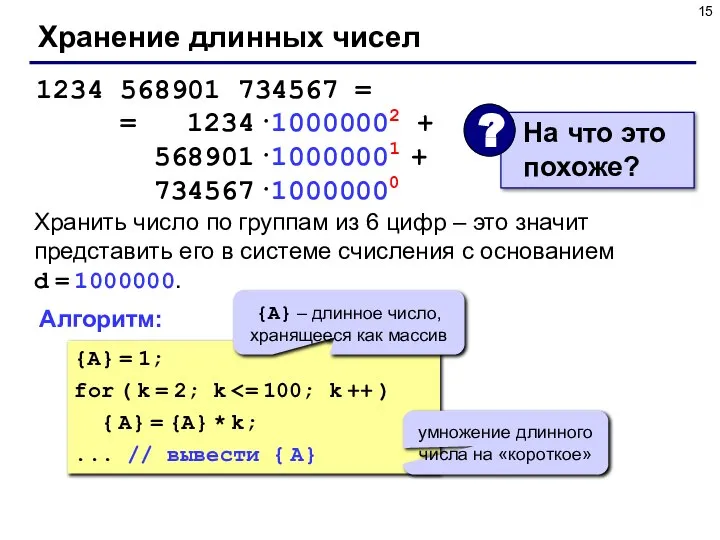
- 15. Хранение длинных чисел 1234 568901 734567 = = 1234·10000002 + 568901·10000001 + 734567·10000000 Хранить число по
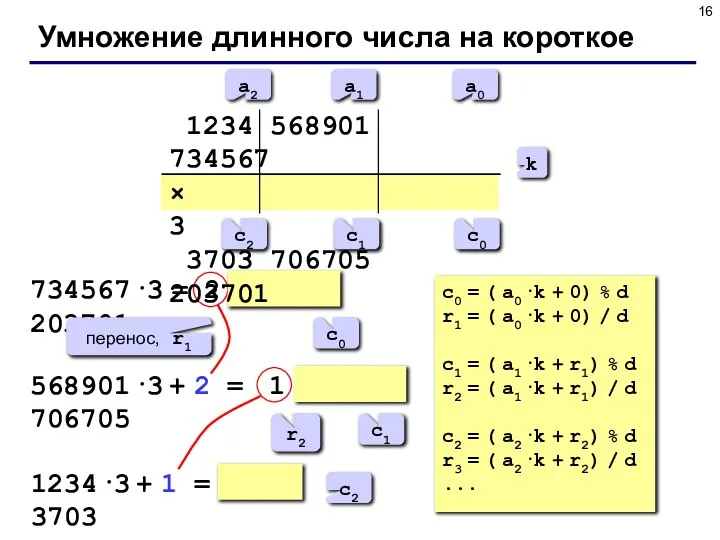
- 16. Умножение длинного числа на короткое 1234 568901 734567 × 3 3703 706705 203701 k a0 a1
- 17. Вычисление 100! const int d = 1000000; // основание системы int A[40] = {1}, // A[0]=1,
- 18. Вариант для С++ #include typedef vector lnum; const int d = 1000000; // основание системы lnum
- 19. Как вывести длинное число? «Первая мысль»: for ( i = len-1; i >= 0; i --
- 20. Вариант для С++ Сначала мы просто выводим самый последний элемент вектора (или , если вектор пустой),
- 21. Задания «4»: Составить программу для вычисления 99!! = 1·3·...·97·99 «5»: То же самое, но написать свою
- 22. Целочисленные алгоритмы (язык Си) Тема 4. Целочисленная оптимизация © К.Ю. Поляков, 2008-2009
- 23. Задачи целочисленной оптимизации Оптимизация: при заданных ограничениях Целочисленная оптимизация: x – вектор (массив) целых чисел Комбинаторная
- 24. Задача коммивояжера Задача коммивояжера. Коммивояжер (бродячий торговец) должен выйти из первого города и, посетив по разу
- 25. Метод случайных перестановок Что представляет собой решение? перестановка чисел 2,3,...N. комбинаторная задача 1 3 5 2
- 27. Скачать презентацию



















 Защита информационных ресурсов компьютерных систем и сетей
Защита информационных ресурсов компьютерных систем и сетей Громадянське суспільство та політичні партії. (Лекция 3)
Громадянське суспільство та політичні партії. (Лекция 3) Презентация "Как начиналась галерея" - скачать презентации по МХК
Презентация "Как начиналась галерея" - скачать презентации по МХК Губка Боб или Спанч Боб - это мультяшный герой, живущий на дне океана в городе Бикини Боттом
Губка Боб или Спанч Боб - это мультяшный герой, живущий на дне океана в городе Бикини Боттом . Лечение угревой болезни
. Лечение угревой болезни Имя существительное
Имя существительное Закономерности, принципы и методы управления персоналом
Закономерности, принципы и методы управления персоналом Расчет токов КЗ в программном комплексе АРМ СРЗА ПК Бриз
Расчет токов КЗ в программном комплексе АРМ СРЗА ПК Бриз Урок 25 Состав числа 11 и соответствующие случаи вычитания
Урок 25 Состав числа 11 и соответствующие случаи вычитания 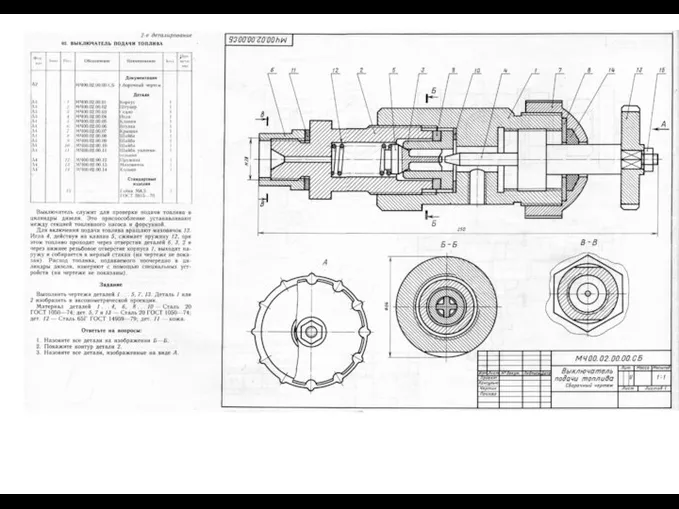 Выключатель подачи топлива. Чертёж
Выключатель подачи топлива. Чертёж Графические возможности Delphi
Графические возможности Delphi Политическая мода и стиль
Политическая мода и стиль Свод знаний по управлению проектами. PMBOK – Project Management Body of Knowledge
Свод знаний по управлению проектами. PMBOK – Project Management Body of Knowledge Патриарх сибирского пейзажа Кондратий Белов
Патриарх сибирского пейзажа Кондратий Белов WM HSG Special Options (룸콘 특수기능). Настройка котла
WM HSG Special Options (룸콘 특수기능). Настройка котла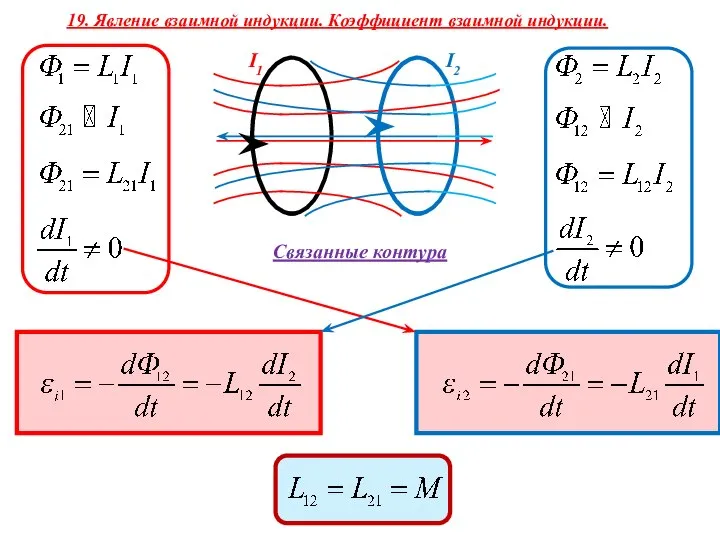 Взаимная индукция. Энергия магн.поля
Взаимная индукция. Энергия магн.поля Нормативно-правовое и нормативно-техническое регулирование в строительстве
Нормативно-правовое и нормативно-техническое регулирование в строительстве Режимы налогообложения. Задание 6
Режимы налогообложения. Задание 6 Основные термины электроники. Полупроводниковые элементы. Полупроводниковые выпрямители
Основные термины электроники. Полупроводниковые элементы. Полупроводниковые выпрямители Доходы государства
Доходы государства Разработка и монтаж электронного блока утечки бытового газа для одного подьезда на базе микроконтроллера Atmega8
Разработка и монтаж электронного блока утечки бытового газа для одного подьезда на базе микроконтроллера Atmega8 Электрощит питания судов с берега. Стартерный пуск судового дизель-генератора. (Билет 13)
Электрощит питания судов с берега. Стартерный пуск судового дизель-генератора. (Билет 13) Презентация Стратегия развития Федеральной таможенной службы до 2020 г
Презентация Стратегия развития Федеральной таможенной службы до 2020 г History of computer development
History of computer development Презентация Цели, задачи и функции государственного управления на современном этапе
Презентация Цели, задачи и функции государственного управления на современном этапе  Презентация "Введение в макроэкономику" - скачать презентации по Экономике
Презентация "Введение в макроэкономику" - скачать презентации по Экономике Олимпийское движение как социальный феномен
Олимпийское движение как социальный феномен Расчет и определение оптимальной комплектации водосточной системы
Расчет и определение оптимальной комплектации водосточной системы