Содержание
- 2. Постановка задачи оптимизации Условия оптимальности. Условная и безусловная оптимизация. Одномерный случай. Примеры алгоритмов и процедур
- 3. Постановка задачи оптимизации Постановка задачи оптимизации начинается с определения набора независимых переменных и обычно включает условия,
- 4. Постановка задачи оптимизации Задачей оптимизации называется задача поиска минимума скалярной функции на множестве значений ее аргумента,
- 5. Постановка задачи оптимизации К задачам на поиск оптимума сводятся многие из проблем математики, системного анализа, техники,
- 6. Постановка задачи оптимизации Курс посвящен вопросам численного поиска оптимума и оптимизационным алгоритмам. При описании оптимизационных алгоритмов
- 7. Классификация оптимизационных задач Подавляющее большинство оптимизационных задач, возникающих на практике, приводятся к стандартному виду. Даже те
- 8. Постановка задачи оптимизации Вначале обсудим весьма широкий класс задач, именуемых нелинейными непрерывными задачами условной оптимизации (NCP).
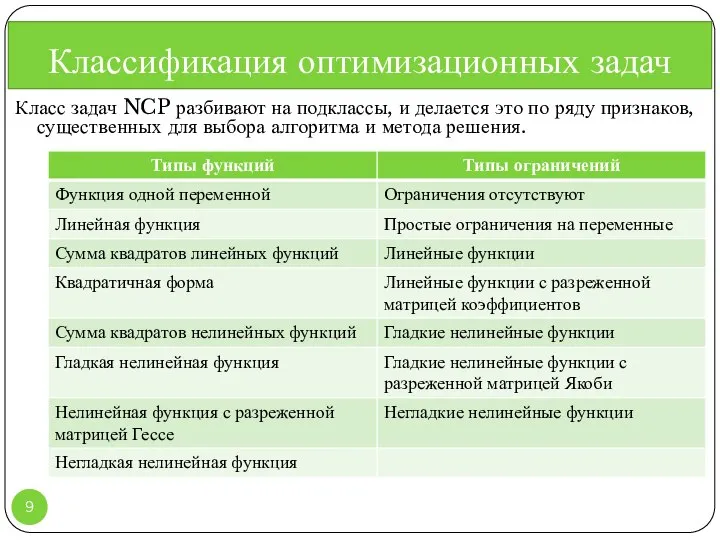
- 9. Класс задач NCP разбивают на подклассы, и делается это по ряду признаков, существенных для выбора алгоритма
- 10. Классификация оптимизационных задач Определим, что понимается под «решением» задачи NCP, и выясним, какими свойствами оно обладает.
- 11. Классификация оптимизационных задач Пусть х*—допустимая точка NCP и через обозначено множество допустимых точек, содержащихся в -окрестности
- 12. В соответствии с данными определениями х* не будет точкой локального минимума, если в любой ее окрестности
- 13. БЕЗУСЛОВНАЯ ОПТИМИЗАЦИЯ Мы начнем изучение условий оптимальности с простейшей задачи о безусловной минимизации функции одной переменной:
- 14. Требование равенства нулю производной называют необходимым условием оптимальности первого порядка. Это условие касается только первой производной.
- 15. Метод золотого сечения. Пусть задана функция Тогда для того, чтобы найти определённое значение этой функции на
- 16. Формализация метода золотого сечения ,
- 17. Троичный поиск , Трои́чный по́иск (Тернарный поиск) — это метод в информатике для поиска максимумов и
- 18. Троичный поиск , function ternarySearch(f, left, right, absolutePrecision) //left and right are the current bounds; the
- 19. Бассейны Ньютона , Бассейны Ньютона для полинома пятой степени. Разными цветами закрашены области притяжения для разных
- 20. Метод Ньютона , Обобщение на комплексную плоскость Метод Ньютона поиска минимума может быть применён и для
- 21. Метод Ньютона , http://en.wikipedia.org/wiki/File:NewtonIteration_Ani.gif http://en.wikipedia.org/wiki/Newton%27s_method
- 22. Опыт – это то, что ты получаешь только тогда, когда в нем нуждаешься … Справочник по
- 23. История Жан Батист Жозеф Фурье (фр. Jean Baptiste Joseph Fourier; 21 марта 1768, Осер, Франция —
- 25. Скачать презентацию





















 Каким должен быть кабинет психолога (идеальная модель)
Каким должен быть кабинет психолога (идеальная модель) Изучение машин и оборудования для организации рельефа и производства дорожных работ
Изучение машин и оборудования для организации рельефа и производства дорожных работ Технология ремонта и проверки стационарной ССМ № 3
Технология ремонта и проверки стационарной ССМ № 3 Презентация на тему "моя воспитательная концепция" - скачать презентации по Педагогике
Презентация на тему "моя воспитательная концепция" - скачать презентации по Педагогике Структура экономической деятельности таможенных органов Выполнили студентки экономического факультета третьего курса группы э1
Структура экономической деятельности таможенных органов Выполнили студентки экономического факультета третьего курса группы э1 Таможенная экспертиза меда
Таможенная экспертиза меда Винсент Виллем ван Гог Слободяник Артём
Винсент Виллем ван Гог Слободяник Артём Договор личного страхования
Договор личного страхования Релейная защита
Релейная защита Растворы ВМС
Растворы ВМС Международные отношения России и Китая
Международные отношения России и Китая Исследование качества жизни подростков 14-17
Исследование качества жизни подростков 14-17 Основы алгоритмизации и быстрое введение в язык Си
Основы алгоритмизации и быстрое введение в язык Си игра правописание гласных 3 класс - презентация для начальной школы
игра правописание гласных 3 класс - презентация для начальной школы Современные компьютерные устройства
Современные компьютерные устройства Политологический анализ демократии
Политологический анализ демократии Тромбоцитопении у детей
Тромбоцитопении у детей Кластер (градостроительство)
Кластер (градостроительство) «Организация процесса самообразования в педагогической деятельности учителя» Автор: заместитель директора по методической раб
«Организация процесса самообразования в педагогической деятельности учителя» Автор: заместитель директора по методической раб b2c32ee31b7d73ec283cb7b321ca54
b2c32ee31b7d73ec283cb7b321ca54 Физиология сердечно- сосудистой системы
Физиология сердечно- сосудистой системы Презентация "Проблема стиля и стилизации в изобразительном искусстве. Рисуем собаку" - скачать презентации по МХК
Презентация "Проблема стиля и стилизации в изобразительном искусстве. Рисуем собаку" - скачать презентации по МХК Основы менеджмента
Основы менеджмента Идеология антикоррупционной политики в России
Идеология антикоррупционной политики в России ООП на Delphi – 5: Элементы ввода и вывода информации. Обработка исключений
ООП на Delphi – 5: Элементы ввода и вывода информации. Обработка исключений Особенности проектирования тепловых сетей в районах с вечномерзлыми грунтами
Особенности проектирования тепловых сетей в районах с вечномерзлыми грунтами Быт знатных людей в древней Руси
Быт знатных людей в древней Руси Трёхсторонний диалог. Инструмент закрытия сделки
Трёхсторонний диалог. Инструмент закрытия сделки