Содержание
- 2. 1.Числовые ряды. Определение. 2.Необходимый признак сходимости. 3.Достаточные признаки сходимости рядов с положительными членами. 4.Знакопеременные ряды. 5.Знакочередующиеся
- 3. Сумма ряда или ряд, — математическое выражение, позволяющее записать бесконечное количество слагаемых и подразумевающее значение их
- 4. Пусть дана бесконечная последовательность чисел: (1) Выражение: (2) называется числовым рядом, а числа - членами ряда.
- 5. Если последовательность частичных сумм имеет конечный предел (3) то этот предел называется суммой ряда. В этом
- 6. Необходимый признак сходимости ряда ● Если ряд сходится, то его общий член к нулю при стремится
- 7. Достаточные признаки сходимости рядов с положительными членами. 1) Признак сравнения рядов (5) (6) ● Если, начиная
- 8. 2) Признак Даламбера. ● Если существует предел то при ℓ ряд (5) сходится , о сходимости
- 9. Примеры 1. Написать пять первых членов ряда по данному общему члену (*) 2. Найти для ряда
- 10. Частичная сумма ряда Отсюда следует, что ряд (*) сходится и его сумма S=1 3. Написать формулу
- 11. Учитывая, что знаки членов ряда чередуются, получим если ,то расходится! => ряд расходится - расходиться! 4.
- 12. 5. Исследовать по признаку Даламбера сходимость ряда: ℓ=0 ряд сходится. 6. Исследовать по признаку Коши сходимость
- 13. Знакопеременные ряды Определение: Если члены числового ряда с разными знаками, то такой ряд будет называться знакопеременным.
- 14. ● Если же ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.
- 15. Знакочередующиеся ряды Ряд (3) (3`) где n>0 (n=1,2,3,…) называется знакочередующимся. Этот ряд является частным случаем знакопеременного
- 16. Признак Лейбница Если члены знакочередующегося ряда (3) убывают по абсолютной величине и 0 , то такой
- 17. Члены данного ряда убывают по абсолютной величине, знаки чередуются и предел =>ряд сходится Составлен ряд (а)
- 18. Итак: 1) Сходятся условно ряды с общим членом или 2) Абсолютно сходятся ряды с общим членом
- 20. Скачать презентацию

















 Етапи розроблення програмного забезпечення
Етапи розроблення програмного забезпечення Cegła
Cegła Логопедическая распевка
Логопедическая распевка Культура Древней Греции
Культура Древней Греции Car body
Car body Создание ресурсного центра по выявлению и поддержке одарённых детей Лицея
Создание ресурсного центра по выявлению и поддержке одарённых детей Лицея Основные способы плавания
Основные способы плавания Interesting places of London
Interesting places of London Жамбыл Жабаев биография
Жамбыл Жабаев биография  Я и закон
Я и закон Организация ЭВМ и вычислительных систем. История развития ВТ и классификация ЭВМ
Организация ЭВМ и вычислительных систем. История развития ВТ и классификация ЭВМ Кальулятор: рассчет стоимости натяжного потолка
Кальулятор: рассчет стоимости натяжного потолка Строительная акустика. Пути повышения изоляции воздушного и ударного шума. Снижение шума в градостроительстве
Строительная акустика. Пути повышения изоляции воздушного и ударного шума. Снижение шума в градостроительстве HALLOWEEN в магазине «Секунда»
HALLOWEEN в магазине «Секунда» Сотрудничество с интернет магазинами
Сотрудничество с интернет магазинами Библейская вера
Библейская вера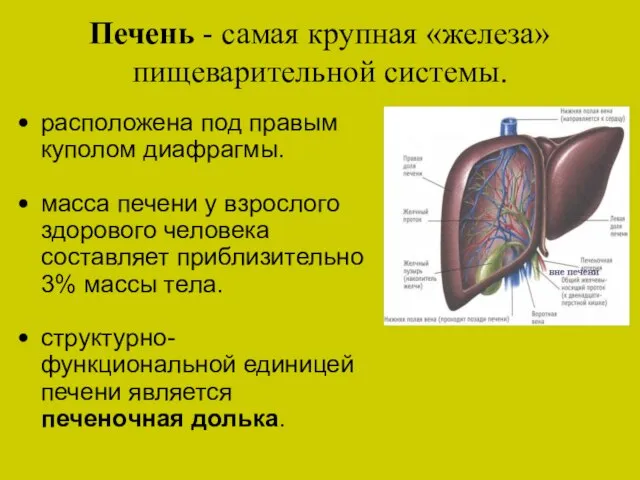 Печень - самая крупная «железа» пищеварительно
Печень - самая крупная «железа» пищеварительно От алгоритма к программе. (Тема 3)
От алгоритма к программе. (Тема 3) Специалист и консультация специалиста. Основы судебной экспертизы
Специалист и консультация специалиста. Основы судебной экспертизы Презентация "Левитан" - скачать презентации по МХК
Презентация "Левитан" - скачать презентации по МХК Презентация Субъекты контроля таможенной стоимости. Функции и полномочия таможенного органа по контролю таможенной стоимости. Ор
Презентация Субъекты контроля таможенной стоимости. Функции и полномочия таможенного органа по контролю таможенной стоимости. Ор История развития лапты
История развития лапты Республика Бурятия
Республика Бурятия Отношения Украины и России
Отношения Украины и России Презентация Усталость. Способы снятия. Выполнили: Фомичёва Татьяна Яценко Яна
Презентация Усталость. Способы снятия. Выполнили: Фомичёва Татьяна Яценко Яна ДОМОНГОЛЬСКИЕ ИКОНЫ
ДОМОНГОЛЬСКИЕ ИКОНЫ История и теория акцизов Выполнили: Минниахметова м.м., Сочнева а.е. Э111б
История и теория акцизов Выполнили: Минниахметова м.м., Сочнева а.е. Э111б Последовательность операций
Последовательность операций