Содержание
- 2. Распространим определения числовых характеристик дискретных величин на величины непрерывные. ♦ Математическим ожиданием непрерывной случайной величины Х,
- 3. ♦ Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если возможные значения Х Є
- 4. Замечание 1. Можно доказать, что св-ва мат. ожидания и дисперсии дискретных величин сохраняются и для непрерывных
- 5. Пример. Найти мат. ожидание и дисперсию случайной величины Х, заданной ф-ей распределения: 0 при х ≤
- 6. Найдем мат. ожидание: M(X) = ∫ x ·1· dx = х2/2 = 1/2. Дисперсия: D(X) =
- 7. Нормальное распределение Нормальным называется распределение вероятностей непр. случ. величины, кот. определяется плотностью f(x) = е -(х-
- 8. Общим называют норм. распределение с произвольными параметрами а и σ (σ>0). Нормированным называют норм. распр-ие с
- 9. Локальная теорема Лапласа При больших значениях n ф-ла Бернулли неудобна, и для приближенных вычислений используют локальную
- 10. Ф-ла тем точнее, чем больше n. Ф-ция φ(x) затабулирована и ее таблица для положительных х приводится
- 11. Интегральная теорема Лапласа Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления
- 12. Спасибо за внимание!
- 13. Нормальная кривая
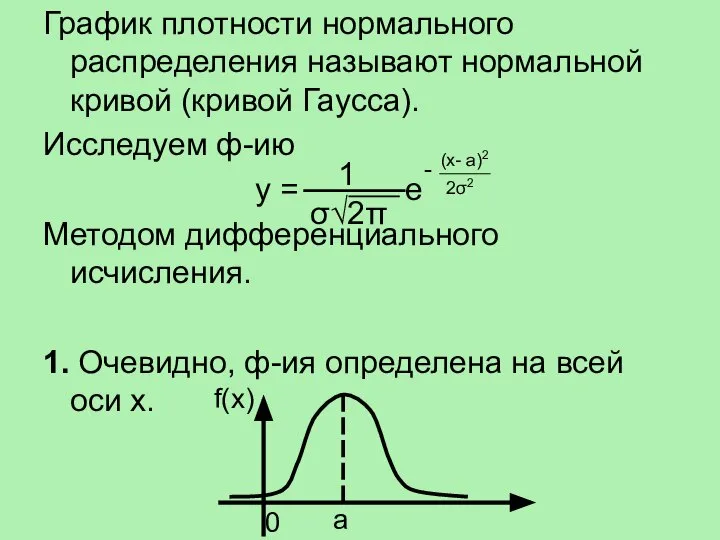
- 14. График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Исследуем ф-ию у = е Методом дифференциального
- 15. 2. у > 0, т.е. кривая расположена над осью х. 3. Lim y = 0, т.е.
- 16. 5. Разность х-а содержится в аналитическом выражении ф-ии в квадрате, т.е. график симметричен относительно прямой х=а.
- 17. у''=0 при х=а±σ, а при переходе через эти точки 2-ая производная меняет знак (в обеих этих
- 18. Влияние параметров нормального распределения на форму нормальной кривой Известно, что график f(x-a) получается параллельным переносом графика
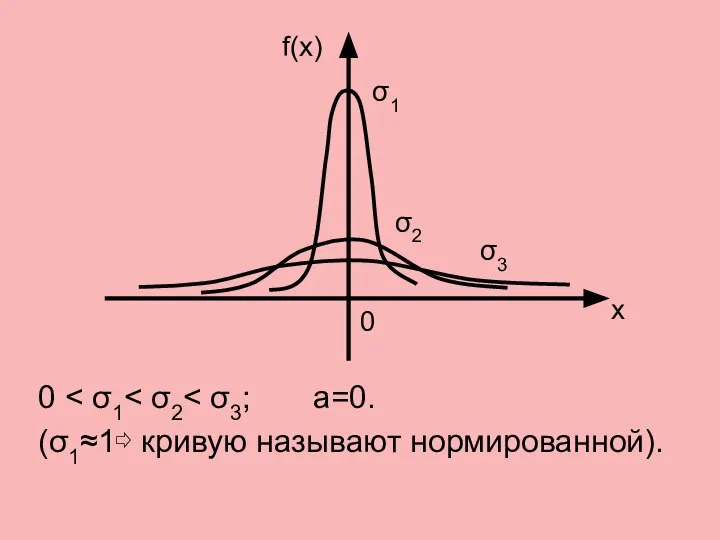
- 19. Отсюда следует, что с возрастанием σ максимум убывает, а сама кривая становиться более пологой, т.е. сжимается
- 20. 0 (σ1≈1⇨ кривую называют нормированной). f(x) х 0 σ1 σ2 σ3
- 21. Вероятность попадания в заданный интервал нормальной случайной величины Как известно P (α того, что случайная величина
- 22. Вычисления вероятности заданного отклонения Часто требуется вычислить вероятность то, что отклонение нормально распределенной случайной величины Х
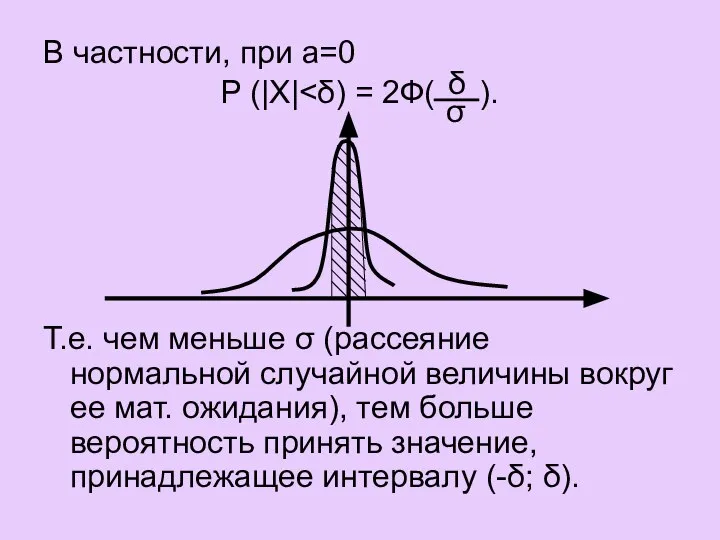
- 23. В частности, при а=0 P (|Х| Т.е. чем меньше σ (рассеяние нормальной случайной величины вокруг ее
- 24. Правило трех сигм В ф-ле P (|Х-а| P (|Х-а| следовательно, σ t = 3σ , то
- 25. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратичное отклонение, очень мала, а
- 26. На практике, если распределение неизвестно, но выполняется условие в правиле 3-х сигм, то есть основание предполагать,
- 28. Скачать презентацию




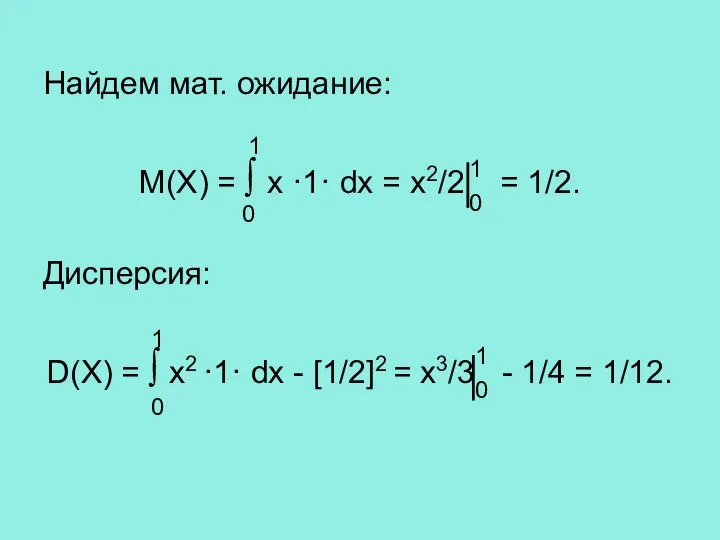

















 Достар
Достар Малая бытовая техника - 2
Малая бытовая техника - 2 Медико-биологические основы физической культуры. Психофизиологические аспекты адаптации человека. (Лекция 3)
Медико-биологические основы физической культуры. Психофизиологические аспекты адаптации человека. (Лекция 3) іс-әрекет - презентация для начальной школы
іс-әрекет - презентация для начальной школы London
London Романо германдық құқықтық отбасының сипаттамасы
Романо германдық құқықтық отбасының сипаттамасы Функции DeVita AP
Функции DeVita AP Архитектура Древней Руси. Культурные достижения Х-ХV веков
Архитектура Древней Руси. Культурные достижения Х-ХV веков Поликонденсационные смолы и пластмассы на их основе
Поликонденсационные смолы и пластмассы на их основе  JavaScript. Top level functions
JavaScript. Top level functions Формы государственного устройства
Формы государственного устройства Основы индустриальной технологии строительного производства
Основы индустриальной технологии строительного производства Логические ошибки Не подключено OpenMP
Логические ошибки Не подключено OpenMP  Откровение вечной картины
Откровение вечной картины Путешествие в прошлое стула (для дошкольников)
Путешествие в прошлое стула (для дошкольников) Плавание. Техники плавания
Плавание. Техники плавания Закон Вернера
Закон Вернера Жанры телевидения
Жанры телевидения Липиды
Липиды  Отчет главы администрации кемского муниципального района о результатах его деятельности
Отчет главы администрации кемского муниципального района о результатах его деятельности Оптимизация запаса в логистике складирования на примере книжного магазина
Оптимизация запаса в логистике складирования на примере книжного магазина Парові двигуни
Парові двигуни Бионика - наука современности
Бионика - наука современности Электрические воздействия на изоляцию
Электрические воздействия на изоляцию Национальный центр искусства и культуры Жоржа Помпиду
Национальный центр искусства и культуры Жоржа Помпиду Брежнев Леонид Ильич
Брежнев Леонид Ильич Логарифмы и их свойства - презентация по Алгебре
Логарифмы и их свойства - презентация по Алгебре Тест по БЖД
Тест по БЖД