Содержание
- 2. Способы задания дискретной случайной величины не являются общими – они неприменимы, например, для непрерывных случайных величин.
- 3. Функцией распределения называют ф-цию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет
- 4. Свойства функции распределения 1. Значения функции распределения принадлежат отрезку [0;1]: 0 ≤ F(x) ≤ 1. 2.
- 5. Пример №1. Случайная величина Х задана функцией распределения 0 при х ≤ -1 F(x) = х/4+1/4
- 6. Решение. Т.к. на интервале (0;2), по условию, F(x) = x/4 + 1/4, то F(2) - F(0)
- 7. Пример №2. Случайная величина Х задана функцией распределения 0 при х ≤ 2 F(x) = 0,5х
- 8. а) P(X б) P(X в) P(X ≥ 3) = ? Т.к. события Х≥3 и X P(X
- 9. Пример №3. Случайная величина Х задана функцией распределения 0 при х ≤ 0 F(x) = х2
- 10. Вероятность того, что Х примет значение xЄ(0,25; 0,75) в одном испытании, равна P(0,25 = х2│ =
- 11. 4. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна 0. Таким образом,
- 12. Но неправильно думать, что равенство 0 вероятности Р(X=х1) означает, что событие X=х1 невозможно (если не ограничиваться
- 13. 5. Если возможные значения случайной величины принадлежат интервалу (a;b), то 1) F(х) = 0 при х
- 14. График функции распределения ] График расположен в полосе, ограниченной прямыми у=0, y=1 (1 свойство). ] При
- 15. ] При х ≤ а ординаты графика равны 0; при х ≥ b ординаты графика равны
- 16. Плотность распределения вероятностей непрерывной случайной величины Способ задания непрерывной случайной величины с помощью ф-ции распределения не
- 17. Плотностью распределения вероятностей непрерывной случайной величины Х называют ф-цию f(х) – первую производную от ф-ции распределения
- 18. Пример. Дана ф-ция распределения непрерывной случайной величины Х 0 при х ≤ 0 F(x) = sinx
- 19. Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а; b), равна определенному
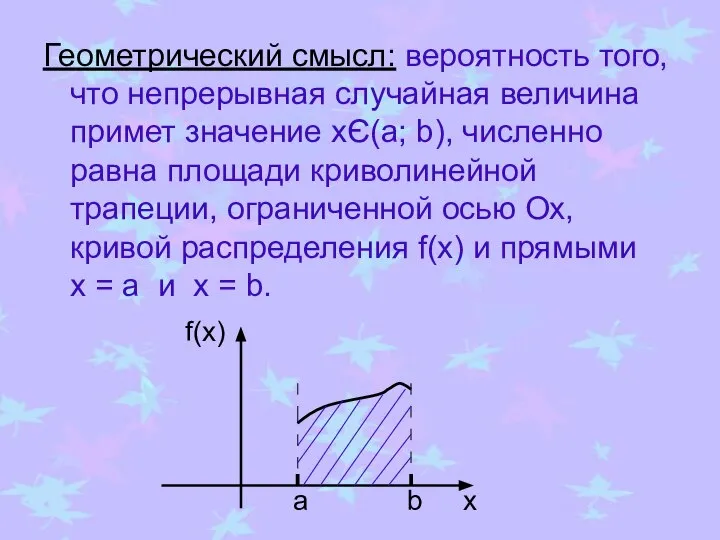
- 20. Геометрический смысл: вероятность того, что непрерывная случайная величина примет значение xЄ(а; b), численно равна площади криволинейной
- 21. Свойства плотности распределения 1. Плотность распределения – неотрицательная функция: f(x) ≥ 0. График плотности распределения называют
- 22. Геометрический смысл: вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна 1. В частности,
- 23. Вероятностный смысл плотности распределения Функция f(x) определяет плотность распределения вероятности для каждой точки х. Для достаточно
- 25. Скачать презентацию


![Свойства функции распределения 1. Значения функции распределения принадлежат отрезку [0;1]: 0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1295510/slide-3.jpg)









![График функции распределения ] График расположен в полосе, ограниченной прямыми у=0,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1295510/slide-13.jpg)
![] При х ≤ а ординаты графика равны 0; при х](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1295510/slide-14.jpg)







 Внешняя политика при Ельцине
Внешняя политика при Ельцине Целевой воспитательный проект по толерантному воспитанию «Астрахань многонациональная», 1 – 11 классы
Целевой воспитательный проект по толерантному воспитанию «Астрахань многонациональная», 1 – 11 классы Окружающая среда. Кино
Окружающая среда. Кино Физиология форменных элементов крови
Физиология форменных элементов крови Тест на знання теорії
Тест на знання теорії родительское собрание Колокольчик
родительское собрание Колокольчик Технология и процесс разработки ПО. Лекция 6
Технология и процесс разработки ПО. Лекция 6 Презентация Транснациональные корпорации и их роль мировом хозяйстве
Презентация Транснациональные корпорации и их роль мировом хозяйстве Организация деятельности по охране труда
Организация деятельности по охране труда ЖИЗНЬ И ТВОРЧЕСТВО Константина Васильевича Иванова РАБОТА УЧЕНИКА МОУ «АТЛАШЕВСКОЙ СОШ» 11 КЛАССА СЕМЕНОВА АЛЕКСАНДРА
ЖИЗНЬ И ТВОРЧЕСТВО Константина Васильевича Иванова РАБОТА УЧЕНИКА МОУ «АТЛАШЕВСКОЙ СОШ» 11 КЛАССА СЕМЕНОВА АЛЕКСАНДРА Міжнародний рух Червоного Хреста і Червоного Півмісяця. Захисні емблеми в праві озброєних конфліктів. (Тема 4)
Міжнародний рух Червоного Хреста і Червоного Півмісяця. Захисні емблеми в праві озброєних конфліктів. (Тема 4) Проектирование программных систем
Проектирование программных систем Презентация "Греческий ордер" - скачать презентации по МХК
Презентация "Греческий ордер" - скачать презентации по МХК Презентация Оползни, сели, обвалы
Презентация Оползни, сели, обвалы Основные понятия из теории надежности и задачи технической диагностики»
Основные понятия из теории надежности и задачи технической диагностики» Презентация Обзор нормативно-правовых актов
Презентация Обзор нормативно-правовых актов  политическая философия Макиавелли - Фадеева,Горковенко
политическая философия Макиавелли - Фадеева,Горковенко Охрана труда ЛИТЕРАТУРА ИЗ ФОНДОВ НТБ: 2006 – 2008 г.
Охрана труда ЛИТЕРАТУРА ИЗ ФОНДОВ НТБ: 2006 – 2008 г. Как найти и не потерять своего клиента
Как найти и не потерять своего клиента Организация обслуживания производства
Организация обслуживания производства Георгафичечкая школа Выполнила: студентка 3-го курса группы Т-083 Восколович Юля.
Георгафичечкая школа Выполнила: студентка 3-го курса группы Т-083 Восколович Юля.  Углубление кризисных явлений в СССР
Углубление кризисных явлений в СССР Suomen kielen tunnit 6 а
Suomen kielen tunnit 6 а Пак О.И., Ульяшин Д.Е.., Блохов А.В. Отделение детской хирургии Краевой клинический центр охраны материнства и детства, г. Владивосто
Пак О.И., Ульяшин Д.Е.., Блохов А.В. Отделение детской хирургии Краевой клинический центр охраны материнства и детства, г. Владивосто Преобразование Барроуза Уилера
Преобразование Барроуза Уилера ТОГУ «Уваровская специальная (коррекционная) общеобразовательная школа-интернат» Индивидуальное коррекционное занятие Учите
ТОГУ «Уваровская специальная (коррекционная) общеобразовательная школа-интернат» Индивидуальное коррекционное занятие Учите Организация и проведение спец операции по пресечению и ликвидации массовый беспорядков
Организация и проведение спец операции по пресечению и ликвидации массовый беспорядков Разминка по теме: «Психология личности преступника» . Подготовила: Студентка 2-го курса ЮФ Группы Юб03/1303 Шестёро Алина
Разминка по теме: «Психология личности преступника» . Подготовила: Студентка 2-го курса ЮФ Группы Юб03/1303 Шестёро Алина