Содержание
- 2. 1. Аналоговые, дискретные и цифровые сигналы Сигна́л — носитель информации, используемый для передачи сообщений в системе
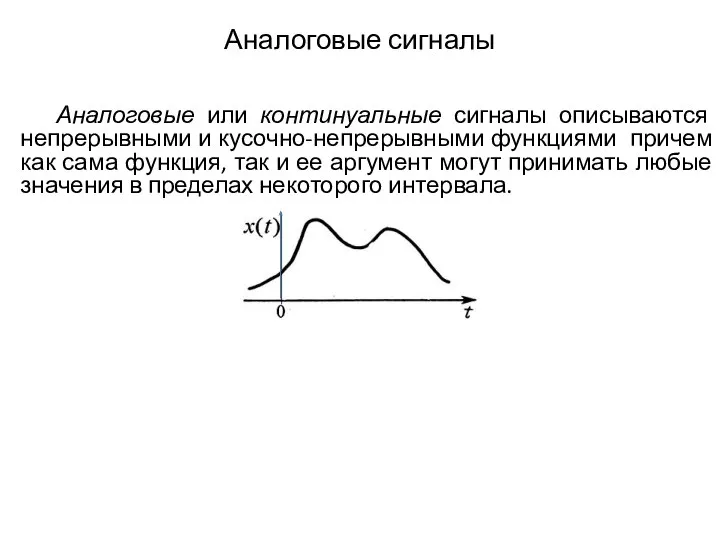
- 3. Аналоговые сигналы Аналоговые или континуальные сигналы описываются непрерывными и кусочно-непрерывными функциями причем как сама функция, так
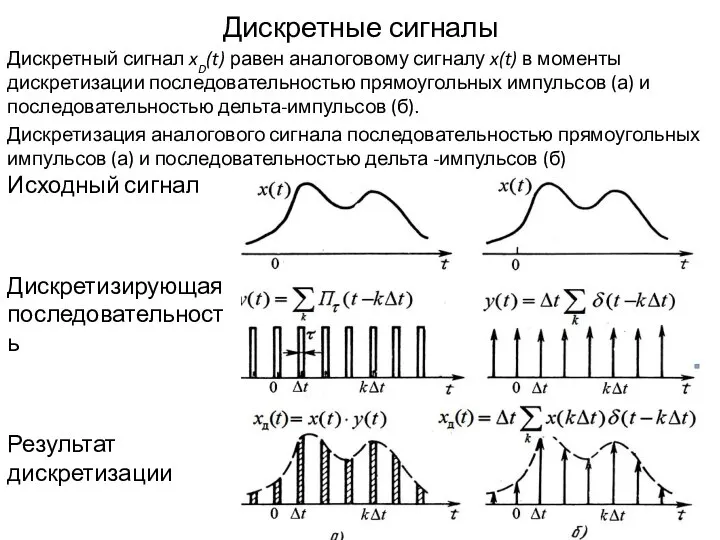
- 4. Дискретные сигналы Исходный сигнал Дискретизирующая последовательность Результат дискретизации Дискретный сигнал xD(t) равен аналоговому сигналу x(t) в
- 5. Цифровые сигналы Цифровой сигнал x(n) иногда называют числовой последовательностью и обозначают xn. Цифровой сигнал получается на
- 6. Примеры последовательностей Единичный импульс δ(n) определяется как последовательность со значениями Единичная ступенчатая последовательность u(n) имеет значения
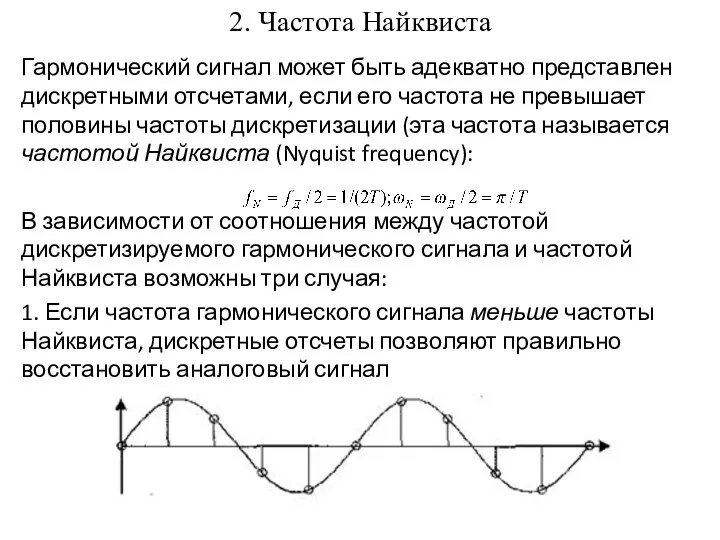
- 7. 2. Частота Найквиста Гармонический сигнал может быть адекватно представлен дискретными отсчетами, если его частота не превышает
- 8. Если частота гармонического сигнала равна частоте Найквиста, то дискретные отсчеты позволяют восстановить аналоговый гармонический сигнал с
- 9. 3. Спектр дискретного сигнала Дискретный сигнал является последовательностью чисел, поэтому для анализа его спектра преобразованием Фурье
- 10. Преобразование Фурье линейно, спектр дельта-функции равен единице, а задержка сигнала во времени приводит к умножению спектра
- 11. 4. Теорема Котельникова Теоре́ма Коте́льникова гласит, что, если аналоговый сигнал x(t) имеет ограниченный спектр, то он
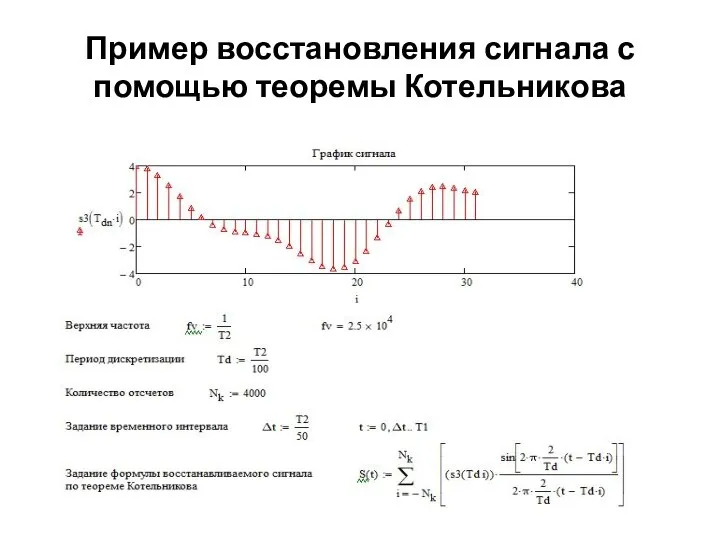
- 12. Пример восстановления сигнала с помощью теоремы Котельникова
- 14. Скачать презентацию







 Родительское собрание 13.05.2015
Родительское собрание 13.05.2015  Многочлены
Многочлены Гидрогеология СЗ РФ
Гидрогеология СЗ РФ  Начертательная геометрия и инженерная графика. (Лекция 1)
Начертательная геометрия и инженерная графика. (Лекция 1) Российская Академия Народного Хозяйства и Государственной Службы При Президенте Российской Федерации Разработка Стратегическо
Российская Академия Народного Хозяйства и Государственной Службы При Президенте Российской Федерации Разработка Стратегическо Технология разработки ПО
Технология разработки ПО Экономическая безопасность государства
Экономическая безопасность государства  Презентация Японская модель рыночной экономики
Презентация Японская модель рыночной экономики Презентация на тему "Ртуть Отравления ртутью Первая медицинская помощь" - скачать презентации по Медицине
Презентация на тему "Ртуть Отравления ртутью Первая медицинская помощь" - скачать презентации по Медицине Политические режимы
Политические режимы Оптическое волокно
Оптическое волокно Вероника Драйер. Художница, общественный деятель, правозащитница. Художественный руководитель центра BAODO
Вероника Драйер. Художница, общественный деятель, правозащитница. Художественный руководитель центра BAODO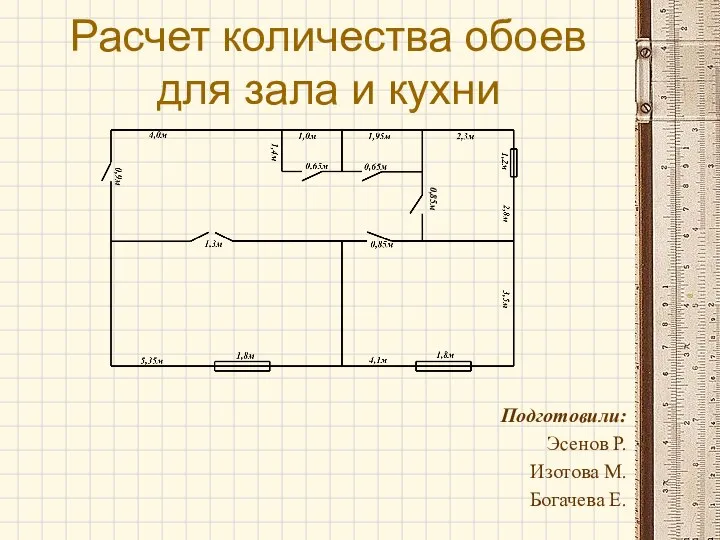 Расчет количества обоев для зала и кухни
Расчет количества обоев для зала и кухни San Petersburgo La Ruta
San Petersburgo La Ruta Презентация
Презентация Народные промыслы России
Народные промыслы России Оператор if
Оператор if Традиции моей семьи Выполнила работу ученица 4г класса сш № 25 Носова Антонина Кл. рук.: Коданева Любовь Владимировн
Традиции моей семьи Выполнила работу ученица 4г класса сш № 25 Носова Антонина Кл. рук.: Коданева Любовь Владимировн Серебряный век Русской культуры
Серебряный век Русской культуры Дневник прохождения производственной практики в «Техно дом» Парк - Отель Прага
Дневник прохождения производственной практики в «Техно дом» Парк - Отель Прага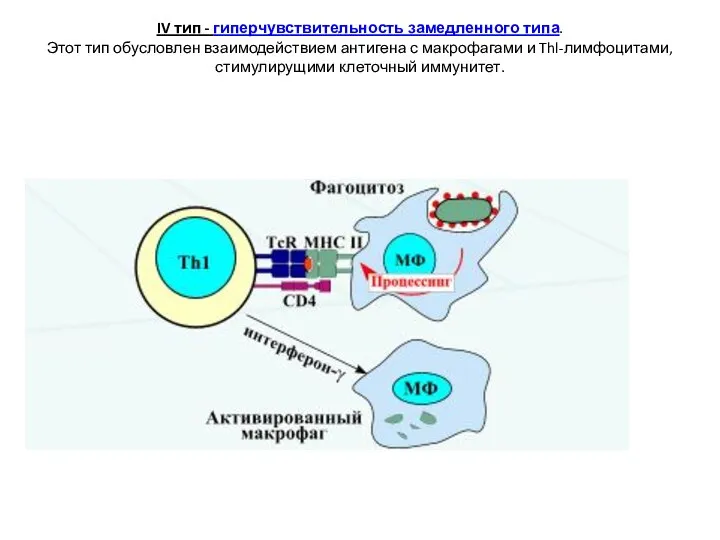 ГЗТ
ГЗТ Тайная вечеря» Леонардо да Винчи.
Тайная вечеря» Леонардо да Винчи.  Объектно-ориентированное программирование
Объектно-ориентированное программирование Либерализм. Взгляды в либерализме
Либерализм. Взгляды в либерализме Субъекты процедур банкротства
Субъекты процедур банкротства Мониторинг в образовании
Мониторинг в образовании  Расчет железобетонной балки. Прямоугольная балка
Расчет железобетонной балки. Прямоугольная балка Совершенствование системы оплаты труда персонала организации
Совершенствование системы оплаты труда персонала организации