Содержание
- 2. Производная функции ОПРЕДЕЛЕНИЕ ПУСТЬ х – ПРИРАЩЕНИЕ АРГУМЕНТА х. ТОГДА х+ х – НОВОЕ ЗНАЧЕНИЕ АРГУМЕНТА,
- 3. ЕСЛИ УКАЗАННЫЙ ПРЕДЕЛ СУЩЕСТВУЕТ, ТО ФУНКЦИЯ f(x) НАЗЫВАЕТСЯ ДИФФЕРЕНЦИРУЕМОЙ В ДАННОЙ ТОЧКЕ х. ЕСЛИ ЖЕ ПРЕДЕЛ
- 4. f'(x) = tg , ГДЕ - УГОЛ НАКЛОНА КАСАТЕЛЬНОЙ М0N (ПРОВЕДЕННОЙ К КРИВОЙ f(x) В ТОЧКЕ
- 5. II. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ ПУСТЬ U’ И V’ СУЩЕСТВУЮТ, Т.Е. ФУНКЦИИ U(x) И V(x)
- 6. III. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ Пусть y = f(u), ГДЕ u = u(x), Т.Е. y = f(u(x))
- 7. 7. (tgU)’ = . U’ 8. (ctgU)’ = - . U’ 9. (arcsinU)’ = . U’
- 8. таблица II C’ = 0, C – const. (Xn)’ = nXn-1 , n – const. (
- 9. IV ПРИМЕРЫ y = X2 -5X + 4 , y - ? y’=(X2 – 5X +
- 10. 2-Й СПОСОБ. ВНАЧАЛЕ РАСКРОЕМ СКОБКИ. y = X5(2- +3X2) = (2X5 - + 3X7 ). ТЕПЕРЬ
- 11. . 6. y = sin6X , y’ - ? y’ = (sin6X)’ = (sinU)’ = cosU
- 13. Скачать презентацию
Производная функции
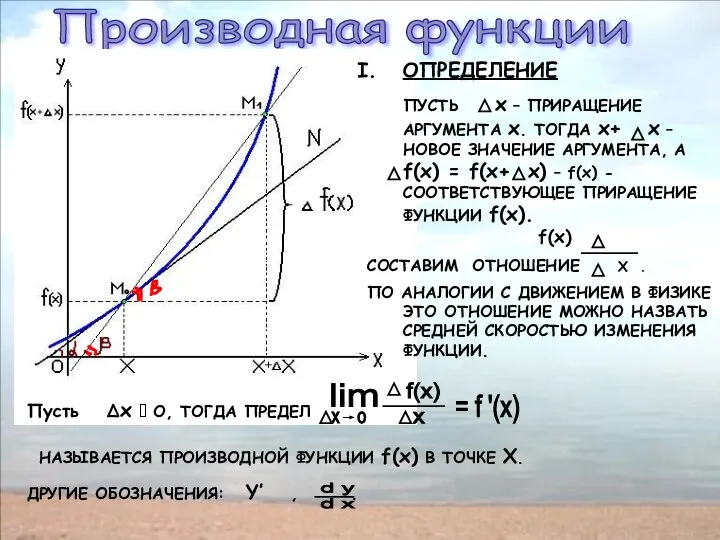
ОПРЕДЕЛЕНИЕ
ПУСТЬ х – ПРИРАЩЕНИЕ АРГУМЕНТА х. ТОГДА х+ х –
Производная функции
ОПРЕДЕЛЕНИЕ
ПУСТЬ х – ПРИРАЩЕНИЕ АРГУМЕНТА х. ТОГДА х+ х –
СОСТАВИМ ОТНОШЕНИЕ Х .
ПО АНАЛОГИИ С ДВИЖЕНИЕМ В ФИЗИКЕ ЭТО ОТНОШЕНИЕ МОЖНО НАЗВАТЬ СРЕДНЕЙ СКОРОСТЬЮ ИЗМЕНЕНИЯ ФУНКЦИИ.
Пусть Δх ? O, ТОГДА ПРЕДЕЛ
НАЗЫВАЕТСЯ ПРОИЗВОДНОЙ ФУНКЦИИ f(x) В ТОЧКЕ Х.
ДРУГИЕ ОБОЗНАЧЕНИЯ: Y’ , .
x o
lim
f(x) x
= f '(x)
d y
d x
ЕСЛИ УКАЗАННЫЙ ПРЕДЕЛ СУЩЕСТВУЕТ, ТО ФУНКЦИЯ f(x) НАЗЫВАЕТСЯ
ДИФФЕРЕНЦИРУЕМОЙ В ДАННОЙ
ЕСЛИ УКАЗАННЫЙ ПРЕДЕЛ СУЩЕСТВУЕТ, ТО ФУНКЦИЯ f(x) НАЗЫВАЕТСЯ
ДИФФЕРЕНЦИРУЕМОЙ В ДАННОЙ
РАВЕН ∞ , ТО ГОВОРЯТ, ЧТО ФУНКИЯ f(x) ИМЕЕТ БЕСКОНЕЧНУЮ ПРОИЗВОДНУЮ.
ДОКАЖЕМ, ЧТО Х’=1.
В ЭТОМ СЛУЧАЕ f(x) = X, f(x+ x) = x+ x.
ПРИРАЩЕНИЕ ФУНКЦИИ f(x) = f(x+ x) – f(x) = X+ X - X = X
СОСТАВИМ ОТНОШЕНИЕ
F(x) X
X X
X’ = lim 1 = 1 ⬄ X’ = 1 , ЧТО И ТРЕБОВАЛОСЬ ДОКАЗАТЬ.
=
f'(x) = tg ,
ГДЕ
- УГОЛ НАКЛОНА КАСАТЕЛЬНОЙ
f'(x) = tg ,
ГДЕ
- УГОЛ НАКЛОНА КАСАТЕЛЬНОЙ
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ПРОИЗВОДНОЙ:
ФИЗИЧЕСКИЙ СМЫСЛ
ПУСТЬ ТЕЛО ДВИЖЕТСЯ ПРЯМОЛИНЕЙНО, И ЗАКОН ЕГО ДВИЖЕНИЯ ПО ВРЕМЕНИ ЗАДАН УРАВНЕНИЕМ S=S(t), ГДЕ S- РАССТОЯНИЕ, ПРОЙДЕННОЕ К МОМЕНТУ ВРЕМЕНИ t. ТОГДА ПРОИЗВОДНАЯ S’(t) ЕСТЬ МНГНОВЕННАЯ СКОРОСТЬ В МОМЕНТ t, Т.Е.
V(t) = S'(t)
II. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
ПУСТЬ U’ И V’ СУЩЕСТВУЮТ,
II. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
ПУСТЬ U’ И V’ СУЩЕСТВУЮТ,
ДИФФЕРЕНЦИРУЕМЫ, ТОГДА
( U + V )’ = U’ + V’
( UV )’ = U’ V + V’ U – ФОРМУЛА ЛЕЙБНИЦА
( )’ = , V ≠ 0
( CU )’ = C U‘ , C – const.
III. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), ГДЕ u = u(x),
III. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Пусть y = f(u), ГДЕ u = u(x),
Y’(x) = f’u(u(x)) . u’(x).
В ЧАСТНОСТИ, ЕСЛИ f(u) – ЭЛЕМЕНТАРНАЯ ФУНКЦИЯ, ТО ПОЛУЧАЕМ ТАБЛИЦУ ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ:
С ’= 0, C – const.
(Un)’= n . Un-1 . U’ , n - const.
( )’ = - . U’
( U)’ = . U’
(sinU)’ = cosU . U’
(cosU)’ = - sinU . U’
ТАБЛИЦА I
№
7. (tgU)’ = . U’
8. (ctgU)’ = - . U’
9. (arcsinU)’
7. (tgU)’ = . U’
8. (ctgU)’ = - . U’
9. (arcsinU)’
10. (arccosU)’ = - . U’
11. (arctgU)’ = . U’
12. (arcctgU)’ = - . U’
13. (аu)’ = аu . lna . U’ , a>O, a≠1
14. (еu)’ = еu . U’
15. (logaU)’ = . U’, a>O, a≠1
16. (lnU)’ = . U’
ЗАМЕЧАНИЕ: ЕСЛИ U = Х, ТО U’= X’=1,a ТАБЛИЦА I УПРОЩАЕТСЯ
1 1-U
2
1 1-U
2
1
1+U
2
1
1+U
2
таблица I /продолжение/
таблица II
C’ = 0, C – const.
(Xn)’ = nXn-1 , n
таблица II
C’ = 0, C – const.
(Xn)’ = nXn-1 , n
( )’= -
( X)’=
(sinX)’ = cosX
(cosX)’ = - sinX
1
Х
2
IV ПРИМЕРЫ
y = X2 -5X + 4 , y - ?
y’=(X2
IV ПРИМЕРЫ
y = X2 -5X + 4 , y - ?
y’=(X2
= 2X – 5.
2. y= 4 X + - , y’ = ?
ПРЕДВАРИТЕЛЬНО ПРЕОБРАЗУЕМ у К СУММЕ СТЕПЕННЫХ ФУНКЦИЙ, ВВОДЯ ДРОБНЫЕ И ОТРИЦАТЕЛЬНЫЕ ПОКАЗАТЕЛИ.
y= X1/4 + 5X-1/3 - X-3. ТЕПЕРЬ y’= X-3/4 + 5(- )X-4/3 –
(-3)X-4 = - +
3. y = X5(2- +3X2) , y’ - ?
1-Й СПОСОБ (ФОРМУЛА ЛЕЙБНИЦА).
y’ = (X5)’.(2- + 3X2)+(2- +3X2)’.X5 =
= 5X4(2- + 3X2) + (6X - ).X5= 10X4- + 15X6 +6X6 - =
= 10X4 – 2X5 + 21X6
1
X
4
5
5
2-Й СПОСОБ. ВНАЧАЛЕ РАСКРОЕМ СКОБКИ.
y = X5(2- +3X2) = (2X5 -
2-Й СПОСОБ. ВНАЧАЛЕ РАСКРОЕМ СКОБКИ.
y = X5(2- +3X2) = (2X5 -
y’ = (2X5 - +3X7)’ = (2X5)’ – ( ) + (3X7)’ =
= 10X4 – 2X5 + 21X6.
4. f(x) = , f’(x) - ?
f’(x) = ( )’= = =
= =
5. y = , y’ = ?
y’= =
= =
= =
6
6
6
2
- (sinX + 2cosX) - (cosX - 2sinX)
(2cosX + sinX)
2
2
2
.
6. y = sin6X , y’ - ?
y’ =
.
6. y = sin6X , y’ - ?
y’ =
7. y = (1+5x)3 , y’ - ?
y’ = ((1 + 5x)3)’ = (U3)’ = 3U2 . U’ = 3(1+5x)2 . (1+5x)’ =
= 15 . (1+5x)2
8. (cos2X)’ = ((cosX)2)’ = (U2)’ = 2U . U’ = 2cosX . (cosX)’ =
= - 2cosX . sinX = - sin2X
9. (esinX2)’ = (eU)’ = eU . U’ = esinX2 . (sinX2)’ = esinX2 . (sinU)’ =
= esinX2 . cosU . U’ = esinX2 . cosX2 . (x2)’ = 2X . esinX2 . cosX2.
- 5
(2cosX + sinX)
2
u
u
u
=
=
=
2









 Тема: « Спряжение глаголов. Закрепление. Ярмарка знаний» Учитель: Переверзева И.В. Класс 4 « А»
Тема: « Спряжение глаголов. Закрепление. Ярмарка знаний» Учитель: Переверзева И.В. Класс 4 « А»  Основные положение конституционного права
Основные положение конституционного права  Бизнес – проект создания детского кафе «Сладкоежка по оказанию услуг детского питания»
Бизнес – проект создания детского кафе «Сладкоежка по оказанию услуг детского питания»  Социальные медиа: маркетинг влияния Антон Попов, Вебинар для Маркетинг Джазз, 2010
Социальные медиа: маркетинг влияния Антон Попов, Вебинар для Маркетинг Джазз, 2010 Литературная экскурсия по улицам города Челябинска
Литературная экскурсия по улицам города Челябинска Христианство. Православие. Часть VI. Русские священники
Христианство. Православие. Часть VI. Русские священники МОЯ БУДУЩАЯ ПРОФЕССИЯ ВОЕННЫЙ
МОЯ БУДУЩАЯ ПРОФЕССИЯ ВОЕННЫЙ  Занятость и безработица 11 класс, экономика, профиль
Занятость и безработица 11 класс, экономика, профиль Информационная безопасность государства
Информационная безопасность государства  ДЕНЬ МИРА
ДЕНЬ МИРА Використання енергії води і вітру
Використання енергії води і вітру Фотообзор районного Фестиваля детского творчества «Радуга талантов» в МАДОУ «Детский сад №317» г. Пермь
Фотообзор районного Фестиваля детского творчества «Радуга талантов» в МАДОУ «Детский сад №317» г. Пермь День народного единства - презентация для начальной школы
День народного единства - презентация для начальной школы Этикет электронной почты Евгений Белошицкий, Отдел развития и инноваций
Этикет электронной почты Евгений Белошицкий, Отдел развития и инноваций Прямые и портфельные инвестиции Выполнили студентки группы Т-116 Хропина Ольга и Фунтикова Виктория
Прямые и портфельные инвестиции Выполнили студентки группы Т-116 Хропина Ольга и Фунтикова Виктория АВТОР ПРОЕКТА: Лукьяненко Ю.В., учитель русского языка и литературы Запорожской гимназии 47, специалист высшей категории, «старший у
АВТОР ПРОЕКТА: Лукьяненко Ю.В., учитель русского языка и литературы Запорожской гимназии 47, специалист высшей категории, «старший у Уголовное законодательство России. История становления и развития
Уголовное законодательство России. История становления и развития ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ ПРОЕКТА СОЗДАНИЯ ПРЕДПРИЯТИЯ ПО ПРОИЗВОДСТВУ КОМПЬЮТЕРОВ
ЭКОНОМИЧЕСКОЕ ОБОСНОВАНИЕ ПРОЕКТА СОЗДАНИЯ ПРЕДПРИЯТИЯ ПО ПРОИЗВОДСТВУ КОМПЬЮТЕРОВ Подготовлено Центром Активации Человека «СОТВОРЕНИЕ» 2011г. - презентация
Подготовлено Центром Активации Человека «СОТВОРЕНИЕ» 2011г. - презентация Разнообразие растений на Земле_
Разнообразие растений на Земле_ Изобразительное искусство и литература
Изобразительное искусство и литература Наши ветераны - презентация для начальной школы_
Наши ветераны - презентация для начальной школы_ Я потеряла питомца
Я потеряла питомца Презентация на тему "Риза" - скачать презентации по Педагогике
Презентация на тему "Риза" - скачать презентации по Педагогике Интернет-технологии – составная часть информатизации сельского хозяйства и аграрной науки В.И. Меденников, доктор технически
Интернет-технологии – составная часть информатизации сельского хозяйства и аграрной науки В.И. Меденников, доктор технически ЖУРНАЛИСТ + НОВЫЕ МЕДИА = МЕЖДУНАРОДНЫЙ ПРОЕКТ Как один журналист может начать международный проект? – Success story фонда WageIndicator Ине
ЖУРНАЛИСТ + НОВЫЕ МЕДИА = МЕЖДУНАРОДНЫЙ ПРОЕКТ Как один журналист может начать международный проект? – Success story фонда WageIndicator Ине Выбор резисторов
Выбор резисторов Презентация на тему "Развитие связной монологической речи у детей старшего возраста через придумывание небылиц и загадок" - с
Презентация на тему "Развитие связной монологической речи у детей старшего возраста через придумывание небылиц и загадок" - с