Содержание
- 2. Лекция 3.1 Дифференцируемость функции в точке. Связь дифференцируемости и непрерывности. Геометрический и физический смысл производной и
- 3. ОПРЕДЕЛЕНИЕ. Функция f(x), определенная в U(x0), называется дифференцируемой в точке х0, если ее приращение при переходе
- 4. Определение производной функции в точке. ОПРЕДЕЛЕНИЕ. Пусть функция f(x) определена в U(x0) и х – произвольная
- 5. ТЕОРЕМА. Для того чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она
- 6. Достаточность. Пусть f(x) имеет производную в точке xo, то есть существует Следовательно Δy /Δx = f
- 7. ЗАМЕЧАНИЕ. Приращение Δх часто обозначают символом dх и называют дифференциалом независимой переменной. Таким образом, дифференциал функции
- 8. ТЕОРЕМА. Если функция f(x) дифференцируема в точке x0, то она непрерывна в этой точке. Доказательство. Пусть
- 9. ЗАМЕЧАНИЕ. Непрерывность функции в точке не является достаточным условием существования в этой точке производной. Пример 1.
- 10. Пример 2. 1 1 - 1 - 1 0 x y → 0 при х →
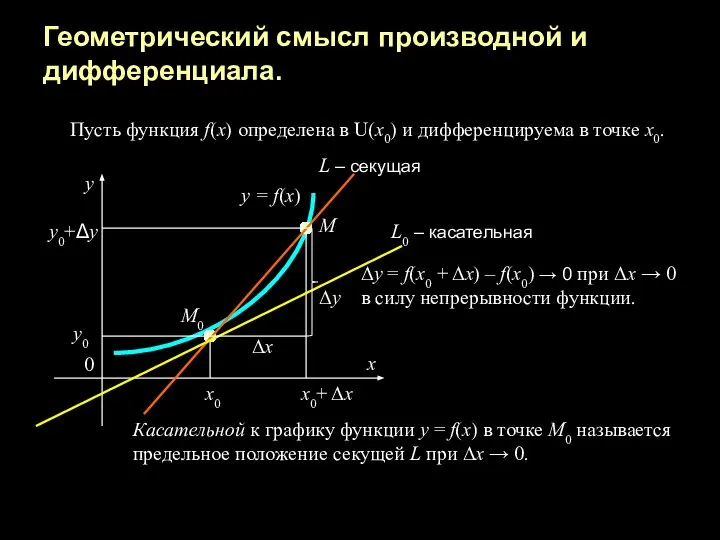
- 11. Геометрический смысл производной и дифференциала. Пусть функция f(x) определена в U(x0) и дифференцируема в точке х0.
- 12. Если функция дифференцируема в точке х0, то в уравнении секущей Δу/Δх → f ′(x0) при Δх
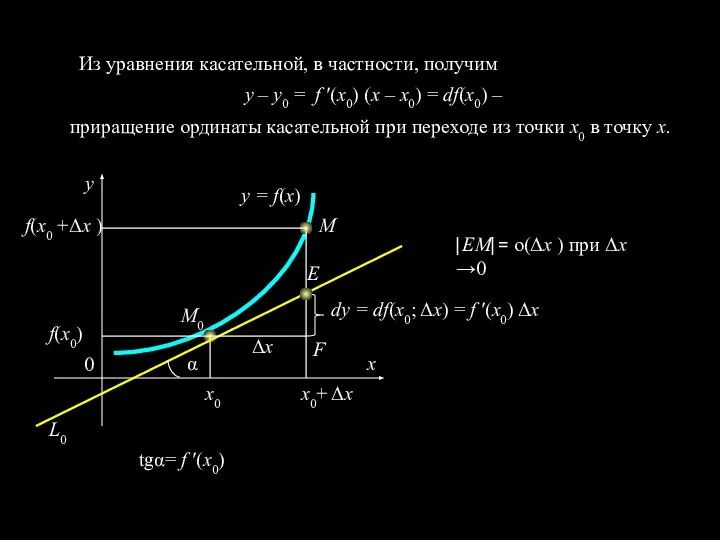
- 13. Из уравнения касательной, в частности, получим у – у0 = f ′(x0) (х – х0) =
- 14. Физические приложения производной и дифференциала. Если S(t) – путь, пройденный материальной точкой за время t, то
- 15. Правила дифференцирования. Дифференцирование суммы, произведения и частного ТЕОРЕМА . Если функции f и g дифференцируемы в
- 16. Пусть у = f⋅g. Тогда Пусть у = f / g. Тогда
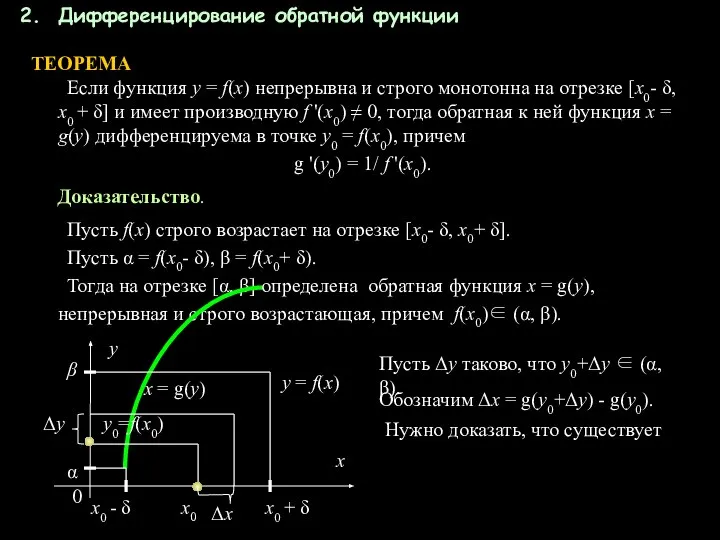
- 17. Дифференцирование обратной функции ТЕОРЕМА Если функция у = f(x) непрерывна и строго монотонна на отрезке [x0-
- 18. Заметим, что Δу ≠ 0, если Δх ≠ 0, в силу строгой монотонности функции. Поэтому при
- 19. Дифференцирование сложной функции ТЕОРЕМА Пусть функция у = f(x) дифференцируема в точке x0, у0 = f(x0),
- 20. Здесь Δх→ 0 при Δt→0 в силу непрерывности функции ϕ (t) в точке t0. при Δt→0.
- 21. СПАСИБО ЗА ВНИМАНИЕ!
- 23. Скачать презентацию

















 Достар
Достар Малая бытовая техника - 2
Малая бытовая техника - 2 Медико-биологические основы физической культуры. Психофизиологические аспекты адаптации человека. (Лекция 3)
Медико-биологические основы физической культуры. Психофизиологические аспекты адаптации человека. (Лекция 3) іс-әрекет - презентация для начальной школы
іс-әрекет - презентация для начальной школы London
London Романо германдық құқықтық отбасының сипаттамасы
Романо германдық құқықтық отбасының сипаттамасы Функции DeVita AP
Функции DeVita AP Архитектура Древней Руси. Культурные достижения Х-ХV веков
Архитектура Древней Руси. Культурные достижения Х-ХV веков Поликонденсационные смолы и пластмассы на их основе
Поликонденсационные смолы и пластмассы на их основе  JavaScript. Top level functions
JavaScript. Top level functions Формы государственного устройства
Формы государственного устройства Основы индустриальной технологии строительного производства
Основы индустриальной технологии строительного производства Логические ошибки Не подключено OpenMP
Логические ошибки Не подключено OpenMP  Откровение вечной картины
Откровение вечной картины Путешествие в прошлое стула (для дошкольников)
Путешествие в прошлое стула (для дошкольников) Плавание. Техники плавания
Плавание. Техники плавания Закон Вернера
Закон Вернера Жанры телевидения
Жанры телевидения Липиды
Липиды  Отчет главы администрации кемского муниципального района о результатах его деятельности
Отчет главы администрации кемского муниципального района о результатах его деятельности Оптимизация запаса в логистике складирования на примере книжного магазина
Оптимизация запаса в логистике складирования на примере книжного магазина Парові двигуни
Парові двигуни Бионика - наука современности
Бионика - наука современности Электрические воздействия на изоляцию
Электрические воздействия на изоляцию Национальный центр искусства и культуры Жоржа Помпиду
Национальный центр искусства и культуры Жоржа Помпиду Брежнев Леонид Ильич
Брежнев Леонид Ильич Логарифмы и их свойства - презентация по Алгебре
Логарифмы и их свойства - презентация по Алгебре Тест по БЖД
Тест по БЖД