Содержание
- 2. ДУ первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
- 3. ДУ 1-го порядка, разрешенное относительно производной:
- 4. Дифференциальная форма ДУ 1-го порядка
- 5. ДУ 1-го порядка с разделяющимися переменными
- 6. ДУ 1-го порядка называется уравнением с разделяющимися переменными, если оно может быть приведено к виду:
- 7. Х1(х)Y(y)
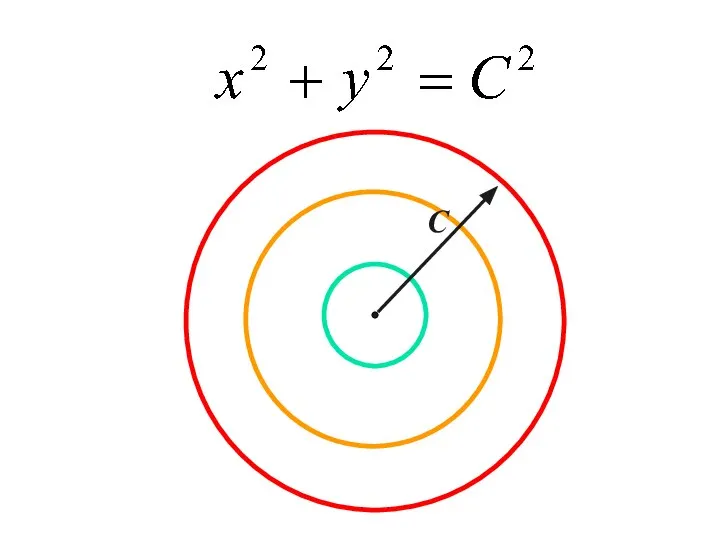
- 8. ПРИМЕР: С2=2С1
- 10. Уравнения, приводящиеся к уравнениям с разделяющимися переменными ДУ вида приводятся к уравнениям с разделяющимися переменными с
- 11. 2. Однородные ДУ 1-го порядка
- 12. Многочлен называется однородным измерения n, если все члены его имеют одно и то же измерение n,
- 13. . ПРИМЕР: однородный многочлен 2-го измерения
- 14. . Замечание: Если аргументы x и y однородного многочлена измерения n заменить на пропорциональные величины kx
- 15. . Функция f (x, y) называется однородной n–го измерения относительно своих аргументов х и у, если
- 16. . Является ли однородной функция ПРИМЕР:
- 17. . Является ли однородной функция ПРИМЕР:
- 18. ДУ 1-го порядка называется однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового
- 20. При dy стоит коэффициент, равный 1, т.е. однородная функция 0-го измерения; следовательно, f (x, y) также
- 21. ДУ 1-го порядка является однородным тогда и только тогда, когда правая часть его f (x, y)
- 22. Замечание: Функция f (x, y) есть однородная функция 0-го измерения, если она не меняется при замене
- 24. Уравнения, приводящиеся к однородным то переменные могут быть разделены подстановкой где α и β - решения
- 25. Уравнения, приводящиеся к однородным то переменные могут быть разделены подстановкой
- 26. 3. Линейные ДУ 1-го порядка
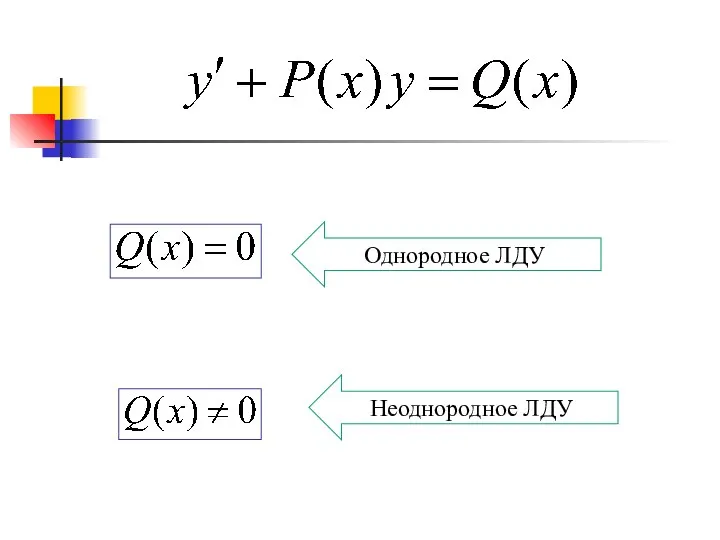
- 27. ДУ называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:
- 28. Однородное ЛДУ Неоднородное ЛДУ
- 29. Линейные однородные ДУ Общее решение
- 30. Линейные неоднородные ДУ Метод Бернулли. 2) Метод Лагранжа. Бернулли Якоб (1654-1705) – швейцарский математик Ларганж Жозеф
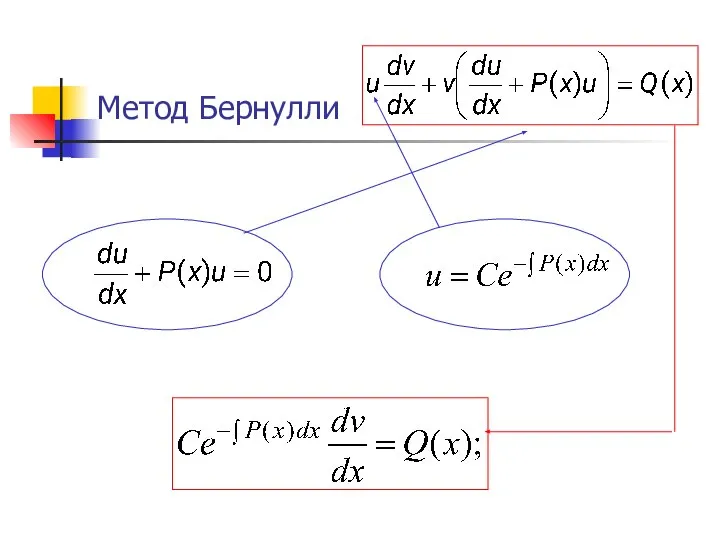
- 31. Метод Бернулли Искомая функция представляется в виде произведения двух функций
- 32. Метод Бернулли Искомая функция представляется в виде произведения двух функций
- 33. Метод Бернулли Важное замечание т.к. первоначальная функция была представлена нами в виде произведения, то каждый из
- 34. Метод Бернулли Таким образом, можно одну из составляющих произведения функций выбрать так, что выражение :
- 35. Метод Бернулли
- 36. Метод Бернулли
- 37. Метод Бернулли ;
- 38. Метод Бернулли ;
- 39. Метод Бернулли ; Решение неоднородного ЛДУ в общем виде по способу Бернулли
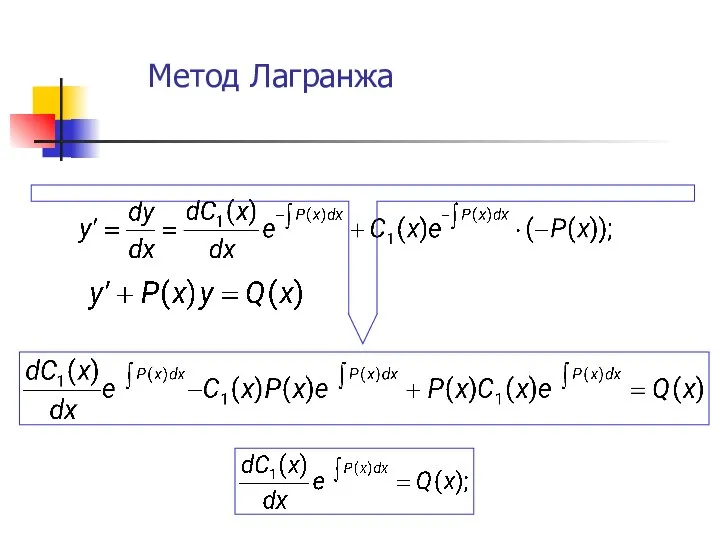
- 40. Метод Лагранжа (вариации произвольной постоянной) 1) Отбросим правую часть:
- 41. Метод Лагранжа 2) Будем считать постоянную С1 некоторой функцией от х.
- 42. Метод Лагранжа
- 43. Метод Лагранжа
- 44. Метод Лагранжа
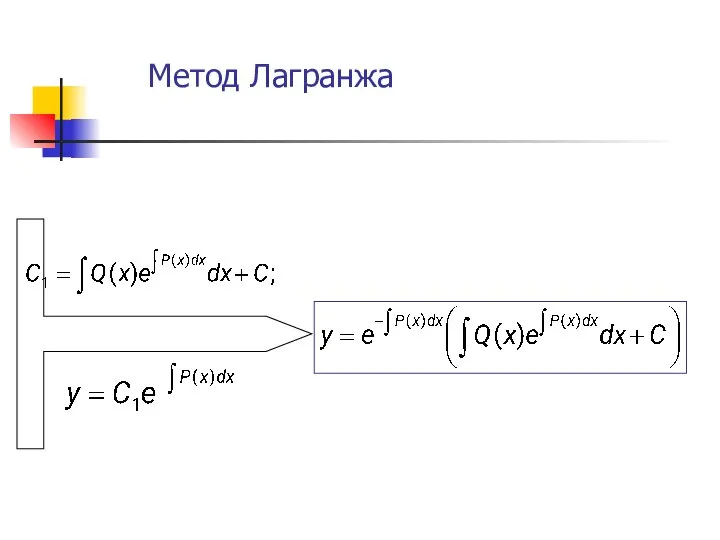
- 45. Метод Лагранжа ; Решение неоднородного ЛДУ в общем виде по способу Лагранжа
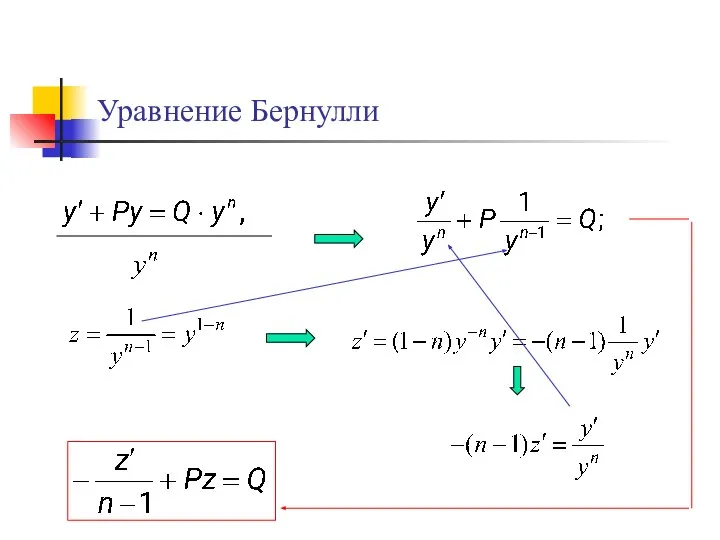
- 46. 4. Уравнения Бернулли
- 47. Уравнение Бернулли где P и Q – функции от х или постоянные числа, а n –
- 48. Уравнение Бернулли применяют подстановку , помощью которой, уравнение Бернулли приводится к линейному
- 49. Уравнение Бернулли
- 50. Уравнение Бернулли линейное уравнение относительно неизвестной функции z
- 53. Скачать презентацию





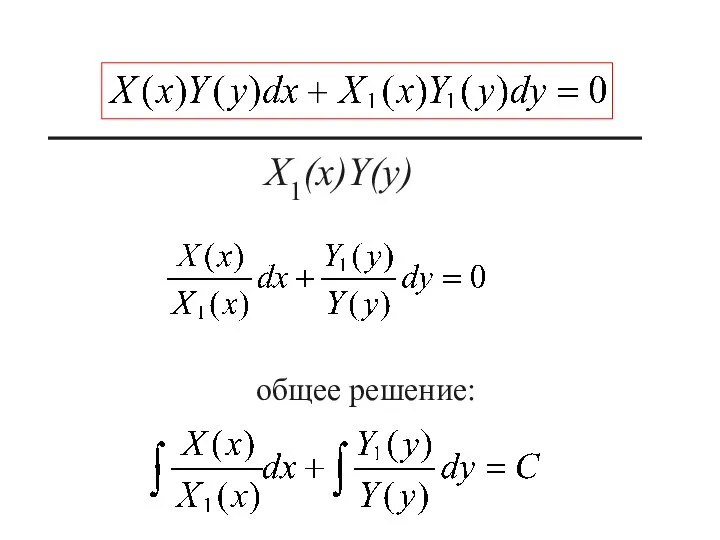






































 Механизм правового регулирования
Механизм правового регулирования METRO. Дизайн для Windows Phone Никита Лукьянец (nikiluk) - презентация
METRO. Дизайн для Windows Phone Никита Лукьянец (nikiluk) - презентация Вербное воскресение. Пасха
Вербное воскресение. Пасха Инженерная графика. Начертательная геометрия. Машиностроительное черчение
Инженерная графика. Начертательная геометрия. Машиностроительное черчение Урок русского языка в 4 классе по теме: «Связь слов в словосочетании. Примыкание.» Выполнила: Суслова Е.А., учитель ГБОУ СОШ №1 гор
Урок русского языка в 4 классе по теме: «Связь слов в словосочетании. Примыкание.» Выполнила: Суслова Е.А., учитель ГБОУ СОШ №1 гор МОУ «Лицей №24 имени Героя Советского Союза А.В. Корявина» Русская матрёшка. Какая она? Учитель начальных классов
МОУ «Лицей №24 имени Героя Советского Союза А.В. Корявина» Русская матрёшка. Какая она? Учитель начальных классов  Вариация признаков. Показатели вариации
Вариация признаков. Показатели вариации Мәңгілік ел – тарих толқынында
Мәңгілік ел – тарих толқынында Конькобежный спорт
Конькобежный спорт  Зачетная работа по риторике. Как интернет влияет на учебу и жизнь человека.
Зачетная работа по риторике. Как интернет влияет на учебу и жизнь человека. Материя (материальное бытие) Выполнила: студентка 1 курса Экономического факультета группы М-122Б Катичева Анна
Материя (материальное бытие) Выполнила: студентка 1 курса Экономического факультета группы М-122Б Катичева Анна «Роль кишечной микрофлоры и пробиотиков в становлении и развитии иммунитета у детей.»
«Роль кишечной микрофлоры и пробиотиков в становлении и развитии иммунитета у детей.» стереотипы и установки
стереотипы и установки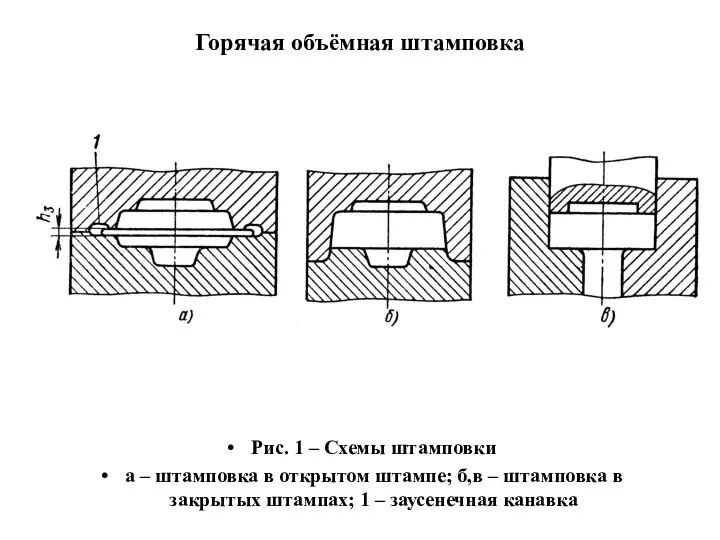 Горячая объёмная штамповка
Горячая объёмная штамповка Парламентские дебаты
Парламентские дебаты Начертательная геометрия. Пересечение поверхности плоскостью общего положения. (Лекция 7)
Начертательная геометрия. Пересечение поверхности плоскостью общего положения. (Лекция 7) Массивы в языке СИ
Массивы в языке СИ Гапонова Стелла
Гапонова Стелла Без названия
Без названия Нечеткие множества
Нечеткие множества  Оздоровитьельная аэробика
Оздоровитьельная аэробика Баскетбол в школе - презентация для начальной школы_
Баскетбол в школе - презентация для начальной школы_ Фотоописание элементов для выступления команд корпоративного черлидинга на Creator Games
Фотоописание элементов для выступления команд корпоративного черлидинга на Creator Games Қазақ халқының ділі
Қазақ халқының ділі Задачи 40-42 по инженерной графике
Задачи 40-42 по инженерной графике Зоны химического заражения
Зоны химического заражения Инфляция и её виды
Инфляция и её виды Фитнес. Тренировочные принципы
Фитнес. Тренировочные принципы