Содержание
- 3. При квантовании по уровню дискретный сигнал принимает значения непрерывного сигнала, соответствующие заданным уровням Реализуется в релейных
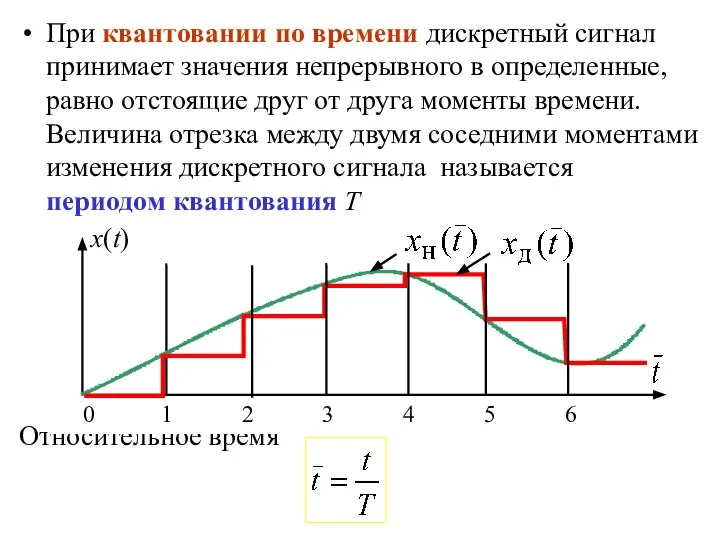
- 4. При квантовании по времени дискретный сигнал принимает значения непрерывного в определенные, равно отстоящие друг от друга
- 5. Квантование по времени осуществляется в импульсных системах Процесс формирования непрерывного сигнала в последовательность импульсов называется модуляцией.
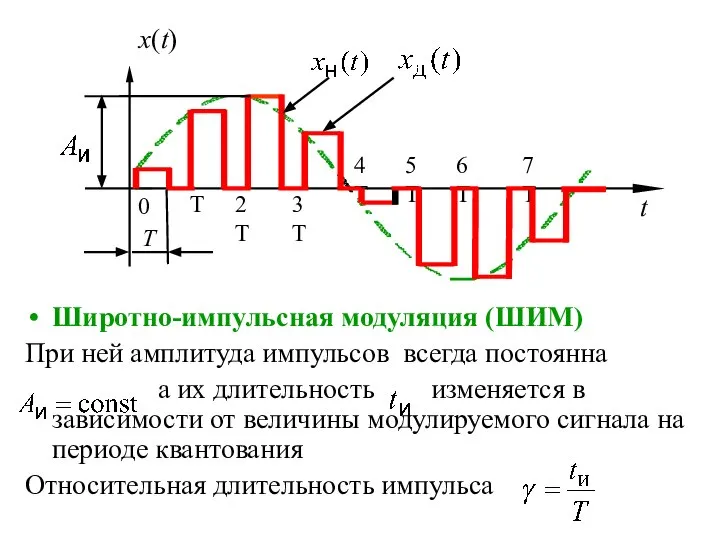
- 6. Широтно-импульсная модуляция (ШИМ) При ней амплитуда импульсов всегда постоянна а их длительность изменяется в зависимости от
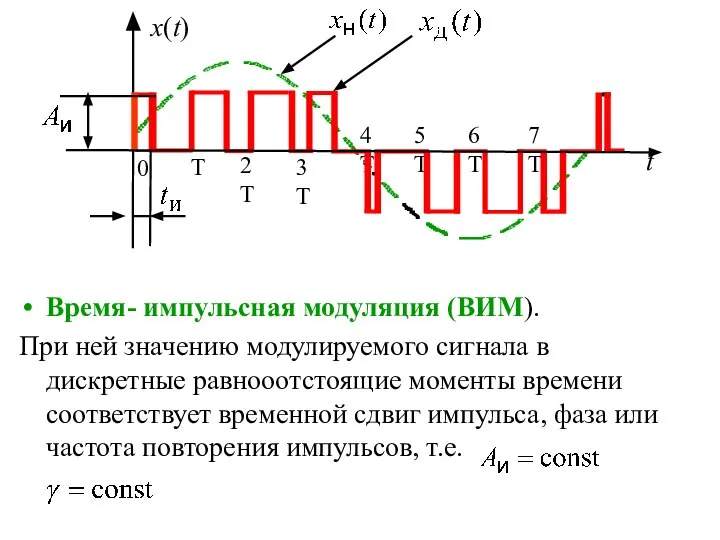
- 7. Время- импульсная модуляция (ВИМ). При ней значению модулируемого сигнала в дискретные равнооотстоящие моменты времени соответствует временной
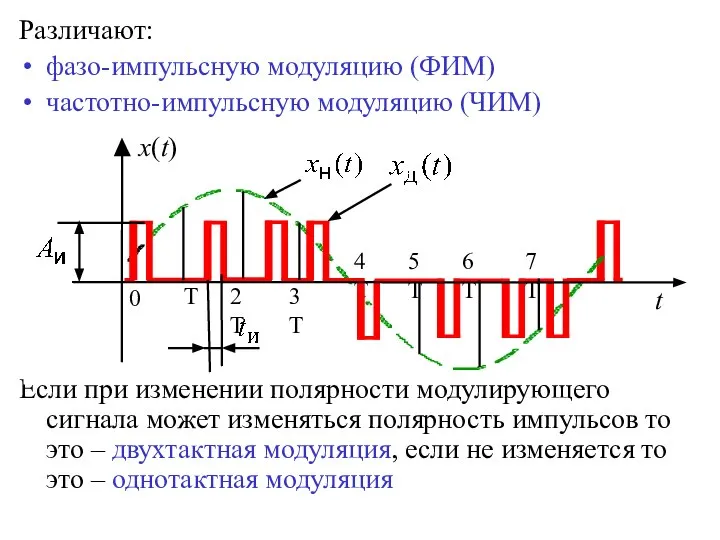
- 8. Различают: фазо-импульсную модуляцию (ФИМ) частотно-импульсную модуляцию (ЧИМ) Если при изменении полярности модулирующего сигнала может изменяться полярность
- 9. Импульсные системы бывают линейными и нелинейными. В линейных импульсных САУ линейными уравнениями описывается как непрерывная часть,
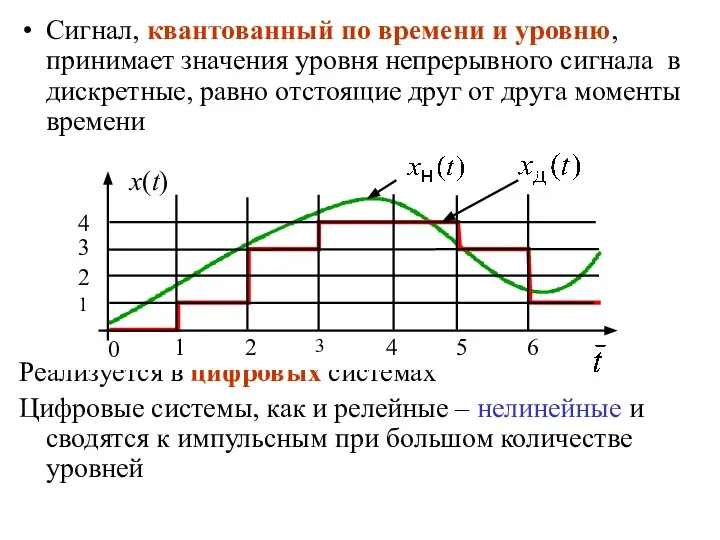
- 10. Сигнал, квантованный по времени и уровню, принимает значения уровня непрерывного сигнала в дискретные, равно отстоящие друг
- 11. ОСНОВЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ САУ С АИМ Понятие решетчатой функции. Разности решетчатых функций и разностные уравнения Функция,
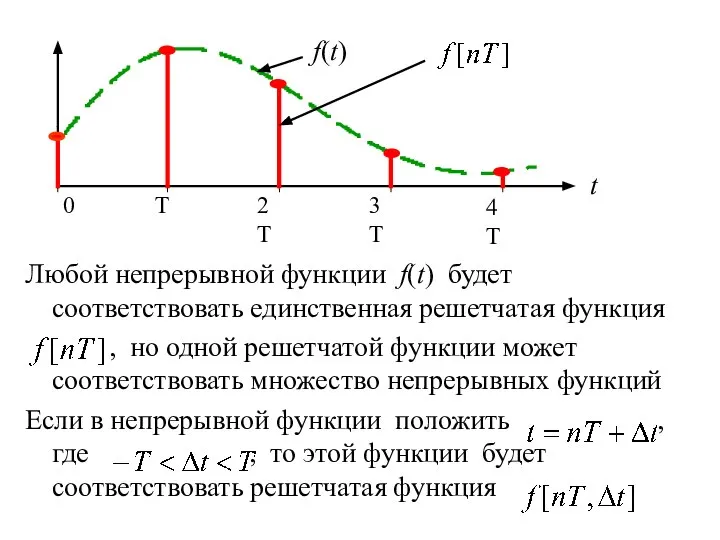
- 12. Любой непрерывной функции f(t) будет соответствовать единственная решетчатая функция , но одной решетчатой функции может соответствовать
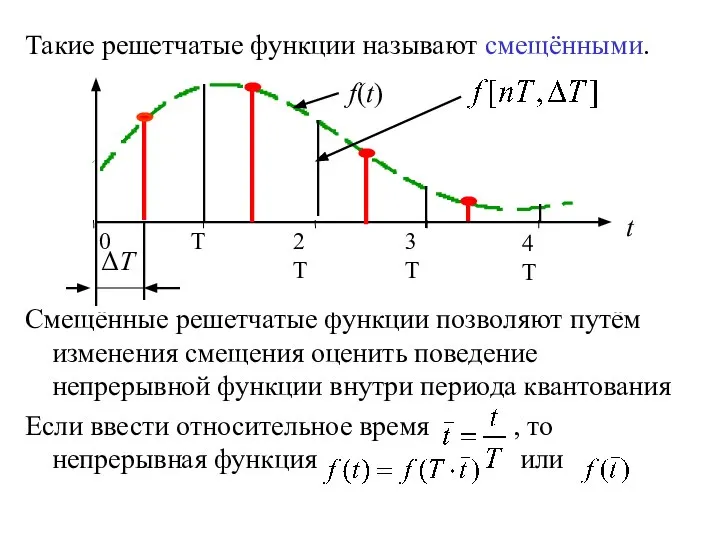
- 13. Такие решетчатые функции называют смещёнными. Смещённые решетчатые функции позволяют путём изменения смещения оценить поведение непрерывной функции
- 14. Ей будет соответствовать решетчатая функция Аналогично для относительного смещения непрерывной функции будет соответствовать смещённая решетчатая функция
- 15. Соотношение между решетчатой функцией и ее разностями различных порядков определяет разностное уравнение. Если эти соотношения линейны,
- 16. Дискретное преобразование Лапласа Дискретное преобразование Лапласа является функциональным преобразованием решетчатых функций и определяется соотношением или где
- 17. Символьная запись дискретного преобразования Лапласа Дискретное преобразование Лапласа устанавливает соответствие между решетчатой функцией и функцией комплексной
- 18. Изображения, полученные с помощью дискретного преобразования Лапласа, будут содержать трансцендентный множитель – функцию вида Если r
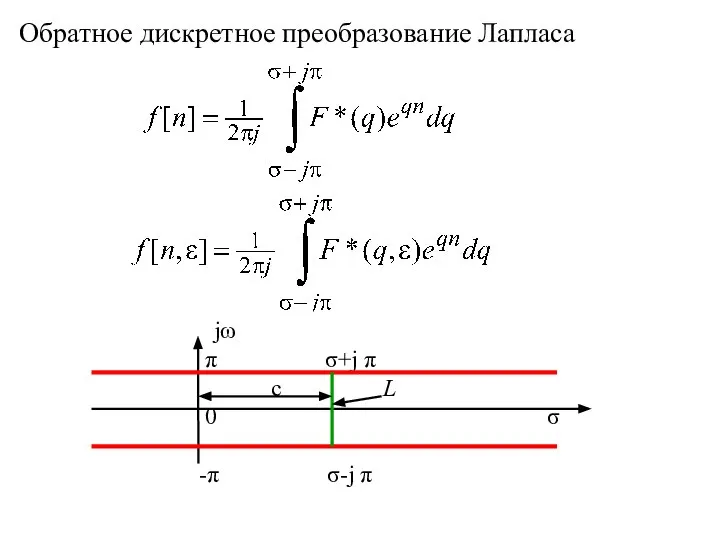
- 19. Обратное дискретное преобразование Лапласа
- 20. Если особые точки изображения расположены правее прямой L, то вычисление интеграла можно произвести через вычеты: Свойства
- 21. Z-преобразование Под z-преобразованием понимают преобразование вила или Функции и можно рассматривать как главную часть ряда Лорана,
- 22. Z-преобразование получается из дискретного преобразования Лапласа путем замены множителя на Обратное Z-преобразование Здесь Г –окружность единичного
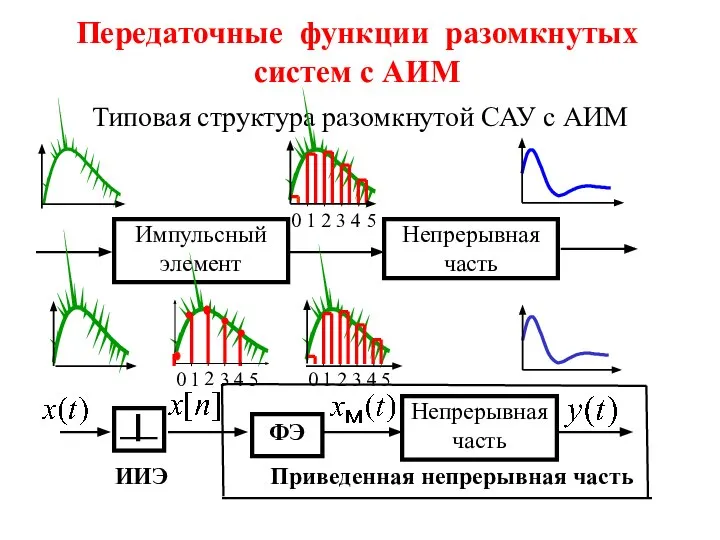
- 23. Передаточные функции разомкнутых систем с АИМ Типовая структура разомкнутой САУ с АИМ
- 24. Здесь: ИИЭ – идеальный импульсный элемент ФЭ – формирующий элемент На выходе ИИЭ в моменты времени
- 25. Импульсная переходная характеристика такого формирующего элемента а его передаточная функция Такой формирующий элемент, называется фиксатором (экстраполятором)
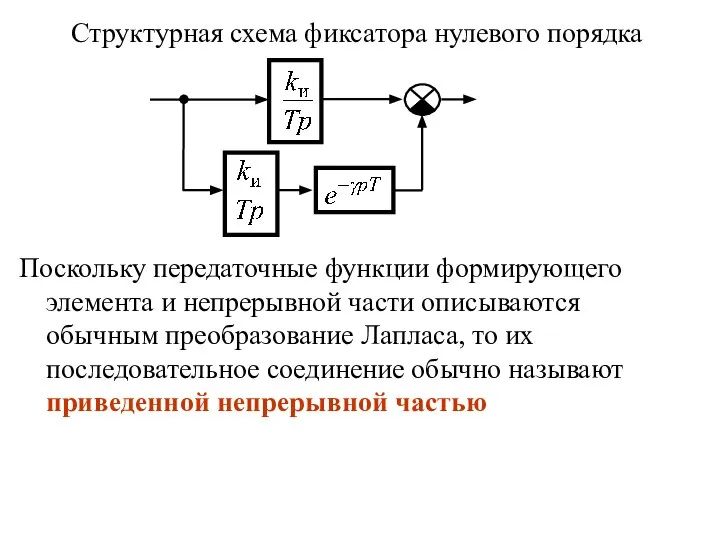
- 26. Структурная схема фиксатора нулевого порядка Поскольку передаточные функции формирующего элемента и непрерывной части описываются обычным преобразование
- 27. Передаточная функция разомкнутой САУ с АИМ В то же время, если – передаточная функция приведённой непрерывной
- 28. Таким образом, передаточная функция разомкнутой системы с АИМ равна передаточной функции ее приведенной непрерывной части в
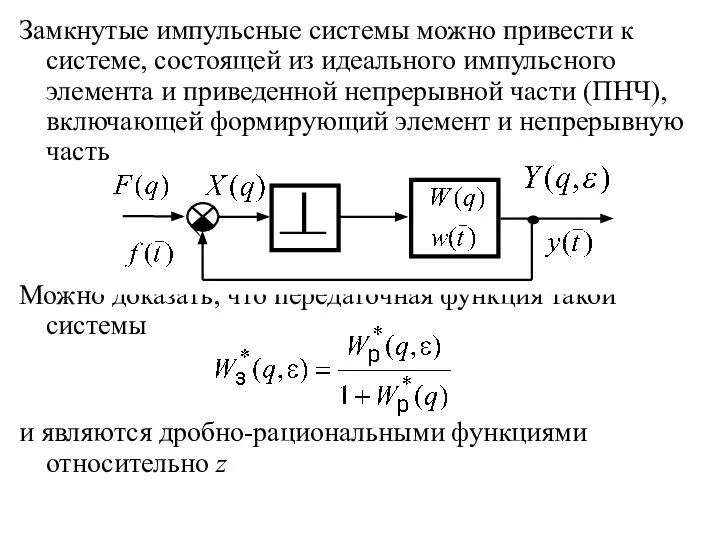
- 29. Замкнутые импульсные системы можно привести к системе, состоящей из идеального импульсного элемента и приведенной непрерывной части
- 30. Частотные характеристики систем с АИМ Поскольку изображение представляет собой периодическую функцию вдоль мнимой оси комплексной плоскости
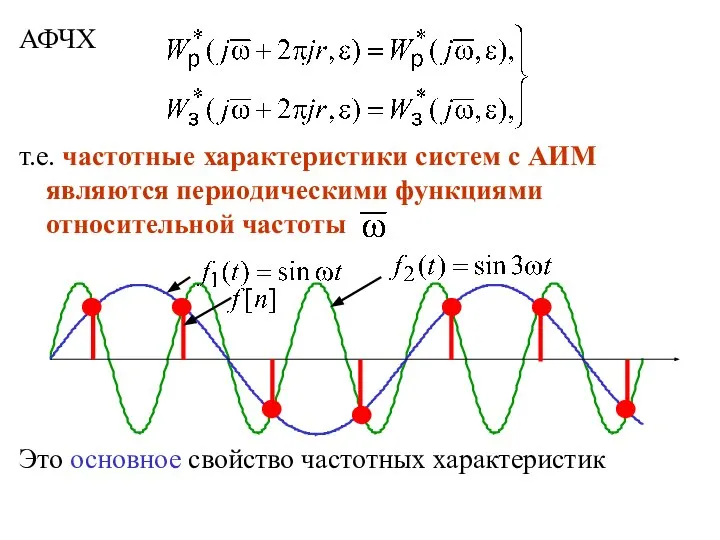
- 31. АФЧХ т.е. частотные характеристики систем с АИМ являются периодическими функциями относительной частоты Это основное свойство частотных
- 32. Другие свойства частотных характеристик САУ с АИМ: Зависимость частотных характеристик от , обычно строят характеристики для
- 33. УСТОЙЧИВОСТЬ СИСТЕМ С АИМ Функция , определяющая закон изменения выходной величины в САУ с АИМ, в
- 34. Составляющая (*) определяет характер переходного процесса и называется переходной составляющей Если при ε = const ,
- 35. Очевидно, что, если полюсы передаточной функции замкнутой системы будут иметь отрицательные вещественные части, то при все
- 36. Таким образом, для того чтобы САУ с АИМ была устойчива, необходимо и достаточно, чтобы все полюсы
- 37. Если САУ описано с помощью модифицированного z-преобразования путём замены , т.е. передаточная функция замкнутой системы принимает
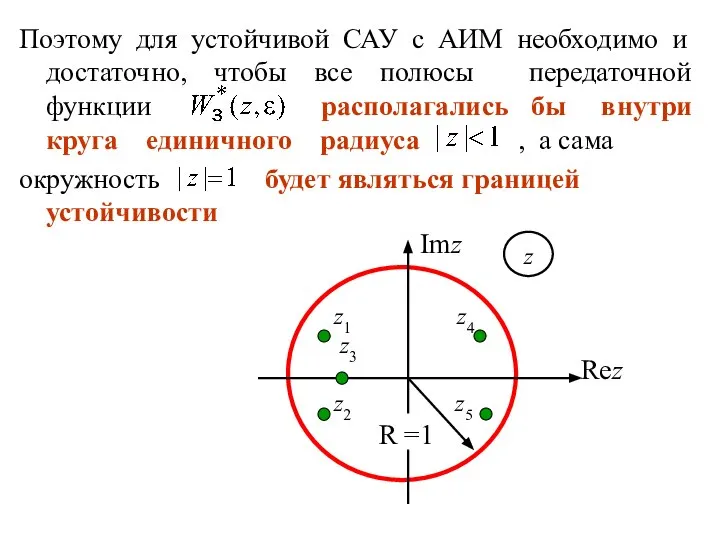
- 38. Поэтому для устойчивой САУ с АИМ необходимо и достаточно, чтобы все полюсы передаточной функции располагались бы
- 39. Анализ устойчивости систем с АИМ Аналог критерия Гурвица Применяется при описании САУ модифицированным z-преобразованием Характеристический полином
- 40. Тогда характеристически полином примет вид или где cj – постоянные коэффициенты Замкнутая система с АИМ будет
- 41. Миноры определителя Гурвица На границе устойчивости Пример: пусть , тогда , причём
- 42. Условия устойчивости САУ: Аналог критерия Михайлова При исследовании устойчивости САУ с АИМ с помощью аналога критерия
- 43. Замкнутая система с АИМ будет устойчива, если при возрастании от 0 до π характеристическая кривая обходит
- 44. Граница устойчивости системы определяется совокупностью параметров, при которых характеристическая кривая проходит через начало координат, т.е. на
- 45. Аналог критерия Найквиста Используется амплитудно-фазовая частотная характеристика (АФЧХ) разомкнутой системы Критерий устойчивости формулируется следующим образом Для
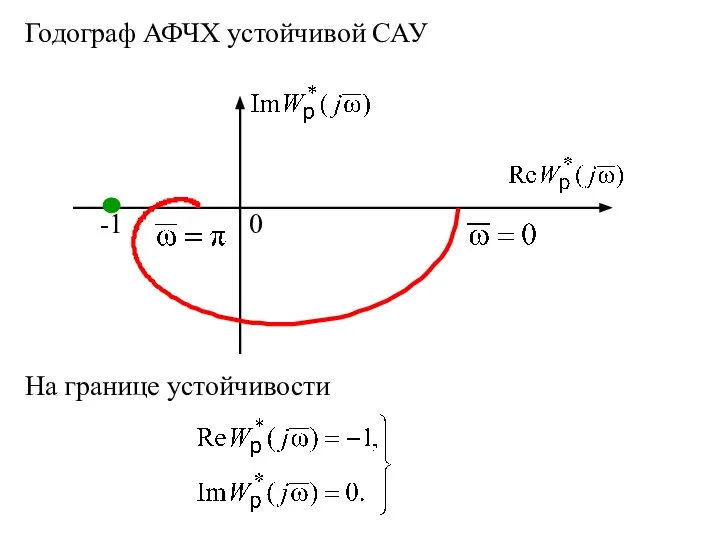
- 46. Годограф АФЧХ устойчивой САУ На границе устойчивости
- 47. Удаление годографа от точки характеризует запасы устойчивости по фазе и амплитуде (модулю, усилению). Запас устойчивости по
- 49. Скачать презентацию
































 VENTURE BUSINESS
VENTURE BUSINESS  Стекло
Стекло Педагогический совет 29.12.2007 Творчески работающий учитель-…
Педагогический совет 29.12.2007 Творчески работающий учитель-… Медицинская информатика и медицинская информация
Медицинская информатика и медицинская информация Антибиотика терапия грибковых заболеваний (на примере кандидамикоза)
Антибиотика терапия грибковых заболеваний (на примере кандидамикоза)  Энзиология
Энзиология  Правописание безударных личных окончаний глаголов - презентация для начальной школы
Правописание безударных личных окончаний глаголов - презентация для начальной школы Решение о стране происхождения товара Выполнили студенты ФТД-5 группы ДС-06 Лепичева Наталия Арутюнян Левон
Решение о стране происхождения товара Выполнили студенты ФТД-5 группы ДС-06 Лепичева Наталия Арутюнян Левон Презентация Приемы работы с пластилином
Презентация Приемы работы с пластилином  ВКР «Влияние занятий гимнастикой пилатес на развитие физических качеств, гибкости и силы у подростков 12-14 лет»
ВКР «Влияние занятий гимнастикой пилатес на развитие физических качеств, гибкости и силы у подростков 12-14 лет» Квазигеострофическая модель умеренных широт
Квазигеострофическая модель умеренных широт Концертная программа
Концертная программа Методы на языке С#
Методы на языке С# Презентация на тему "Современный УМК как средство опережающего развития школьников в условиях обновления содержания образован
Презентация на тему "Современный УМК как средство опережающего развития школьников в условиях обновления содержания образован Внеклассное занятие Внеклассное занятие Любимые сказки о животных.
Внеклассное занятие Внеклассное занятие Любимые сказки о животных. Щелочно-кислотное равновесие. Биохимия мочи.
Щелочно-кислотное равновесие. Биохимия мочи. Русский бидермейер
Русский бидермейер Партийная система Китайской Народной Республики
Партийная система Китайской Народной Республики Презентация ФСКН РФ
Презентация ФСКН РФ АЛГЕБРА 7 КЛАСС Решение систем линейных уравнений
АЛГЕБРА 7 КЛАСС Решение систем линейных уравнений Юридическая техника в Финляндии
Юридическая техника в Финляндии Либерализм, консерватизм, марксизм
Либерализм, консерватизм, марксизм Создание консольного приложения с текстовым меню
Создание консольного приложения с текстовым меню Резьбы
Резьбы Успешная рекомендация Вэлнэс
Успешная рекомендация Вэлнэс Система знаний о мире (в гипотезах, аксиомах, теоремах, законах, принципах, понятиях, теориях) Система знаний о мире (в гипотезах, ак
Система знаний о мире (в гипотезах, аксиомах, теоремах, законах, принципах, понятиях, теориях) Система знаний о мире (в гипотезах, ак Национальные символы весенних праздников
Национальные символы весенних праздников Иммунитет и здоровье
Иммунитет и здоровье