Содержание
- 2. Литература: 1. Зевеке Г.В., Ионкин А.В., Страков С.В. Основы теории цепей: Учебник для вузов, - М.:
- 3. 1. Основные определения и примеры несинусоидальных колебаний в электрических цепях Периодическими несинусоидальными колебаниями называются токи (напряжения),
- 4. При рассмотрении периодических несинусоидальных колебаний обычно пользуются математическим аппаратом - рядом Фурье. Любая периодически изменяющаяся величина
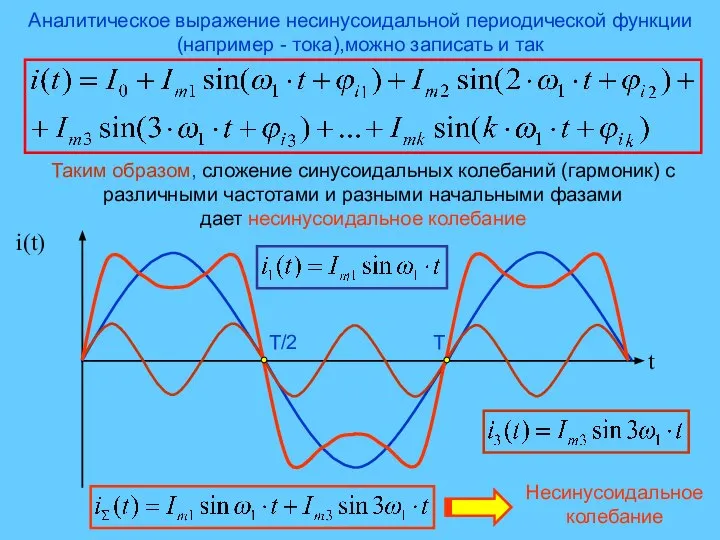
- 5. Аналитическое выражение несинусоидальной периодической функции (например - тока),можно записать и так Таким образом, сложение синусоидальных колебаний
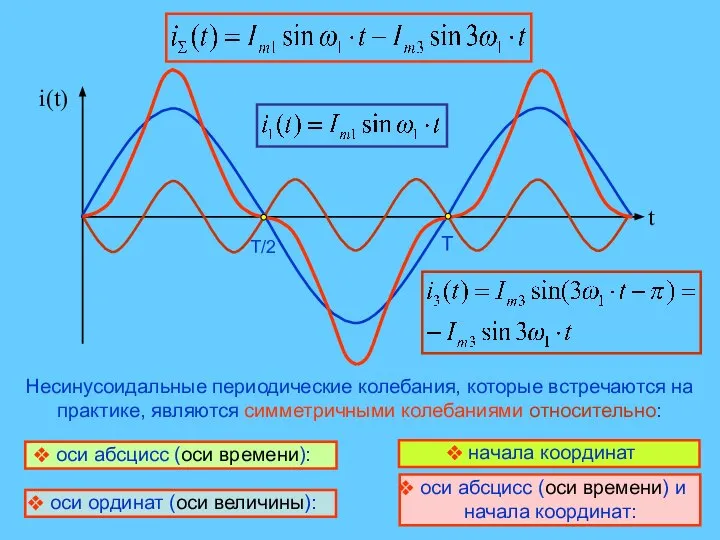
- 6. Несинусоидальные периодические колебания, которые встречаются на практике, являются симметричными колебаниями относительно: оси абсцисс (оси времени): оси
- 7. Периодические колебания симметричные относительно оси абсцисс (оси времени) и начала координат: Колебание типа «меандр» Постоянная составляющая
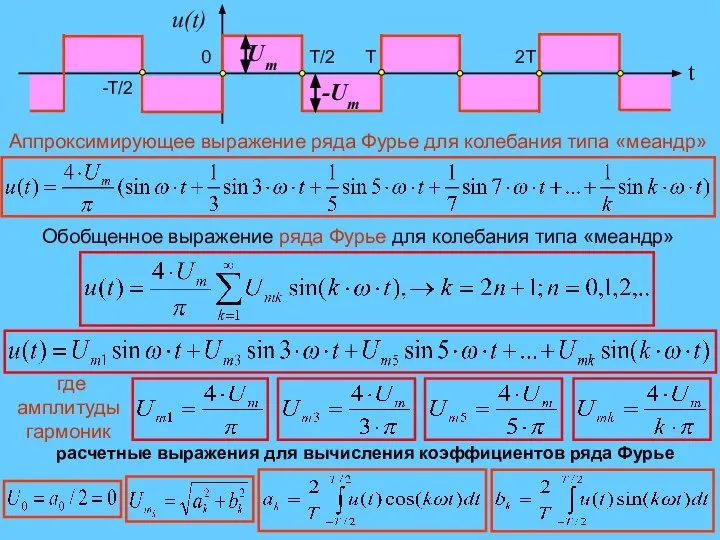
- 8. Аппроксимирующее выражение ряда Фурье для колебания типа «меандр» Обобщенное выражение ряда Фурье для колебания типа «меандр»
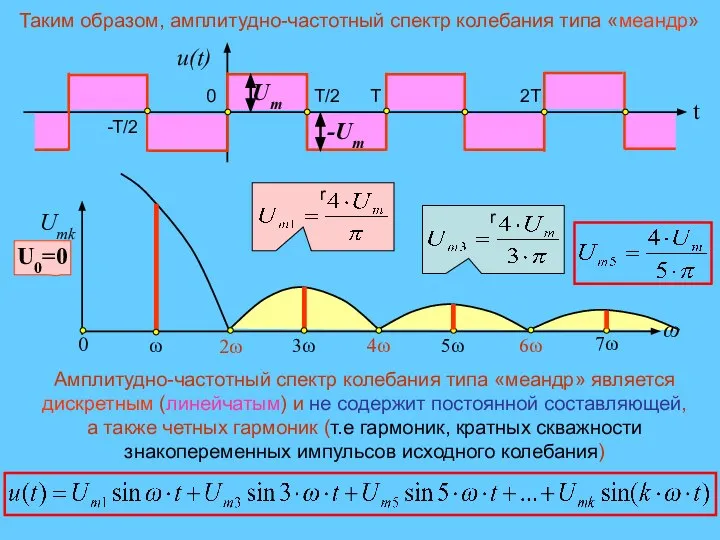
- 9. Таким образом, амплитудно-частотный спектр колебания типа «меандр» U0=0 Амплитудно-частотный спектр колебания типа «меандр» является дискретным (линейчатым)
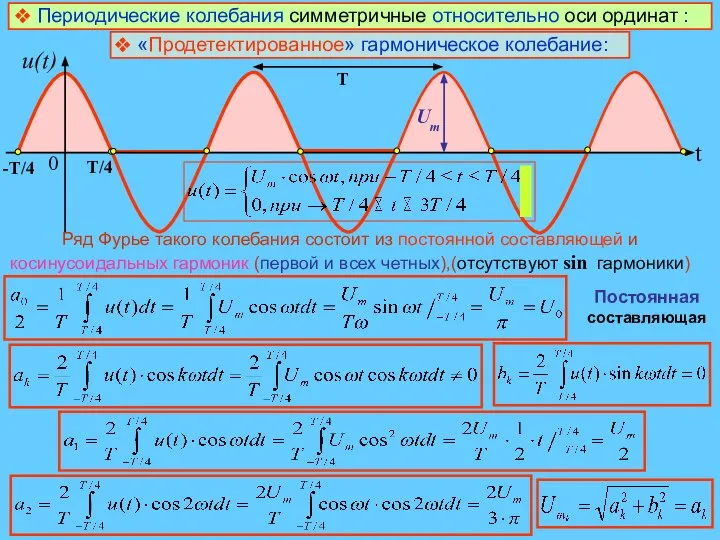
- 10. Периодические колебания симметричные относительно оси ординат : «Продетектированное» гармоническое колебание: Ряд Фурье такого колебания состоит из
- 11. Воспользоваться формулой преобразования произведения тригонометрических функций в сумму Аналитическая запись ряда Фурье такого несинусоидального колебания
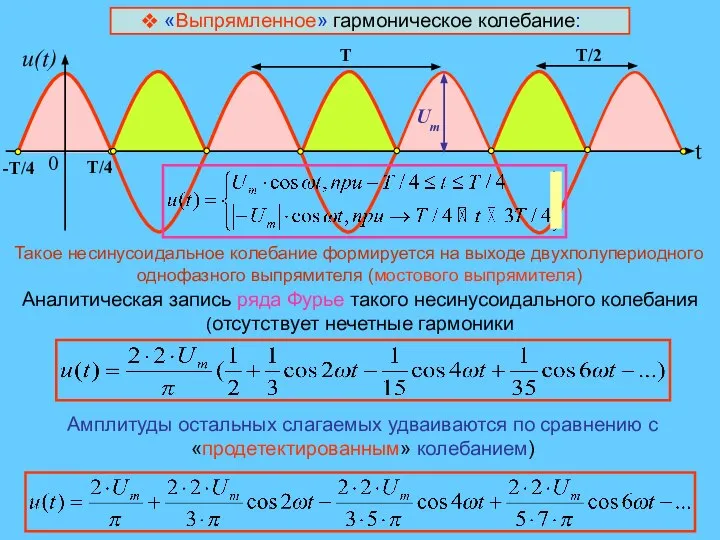
- 12. «Выпрямленное» гармоническое колебание: Такое несинусоидальное колебание формируется на выходе двухполупериодного однофазного выпрямителя (мостового выпрямителя) Аналитическая запись
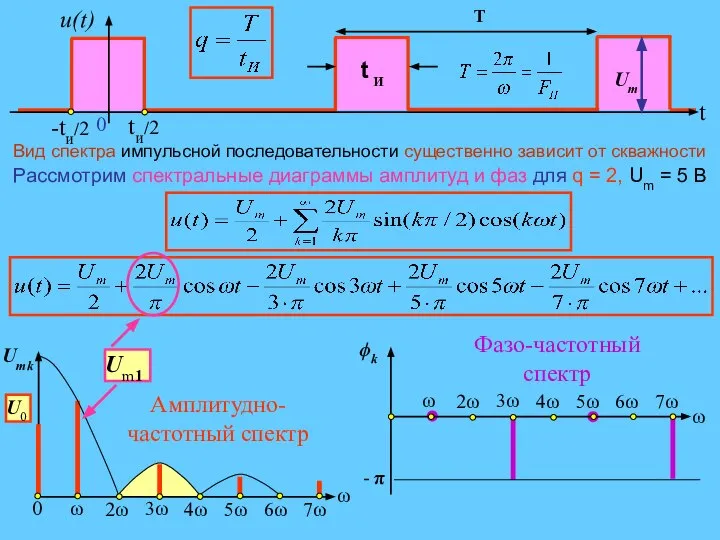
- 13. Периодическая последовательность прямоугольных импульсов: Формы аналитической запись такого несинусоидального колебания Основные параметры импульсной последовательности Период следования
- 14. Коэффициенты разложения ряда Фурье При этом амплитуды гармоник ряда Фурье и их фазы выражаются как: Таким
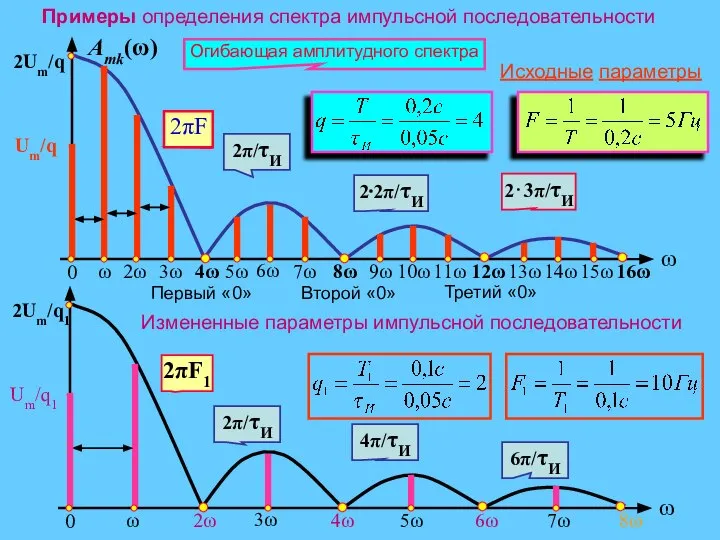
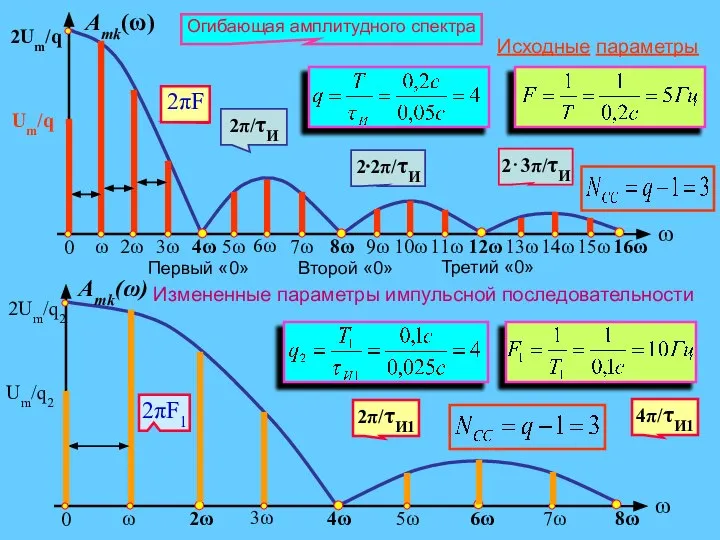
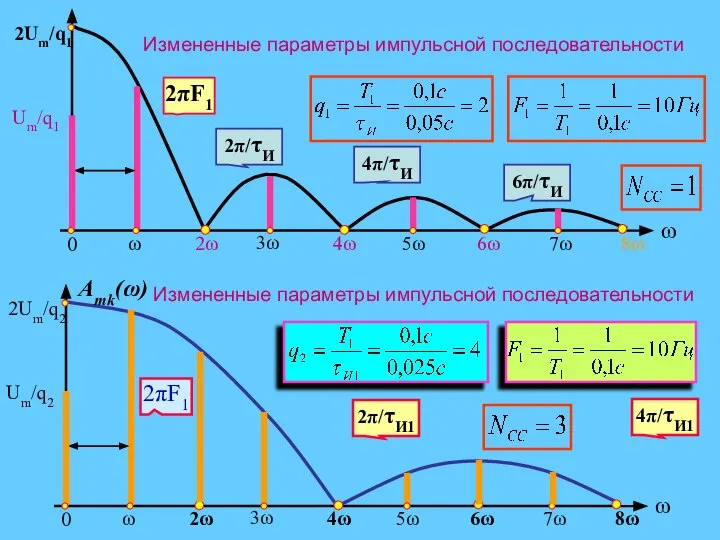
- 15. Вид спектра импульсной последовательности существенно зависит от скважности Рассмотрим спектральные диаграммы амплитуд и фаз для q
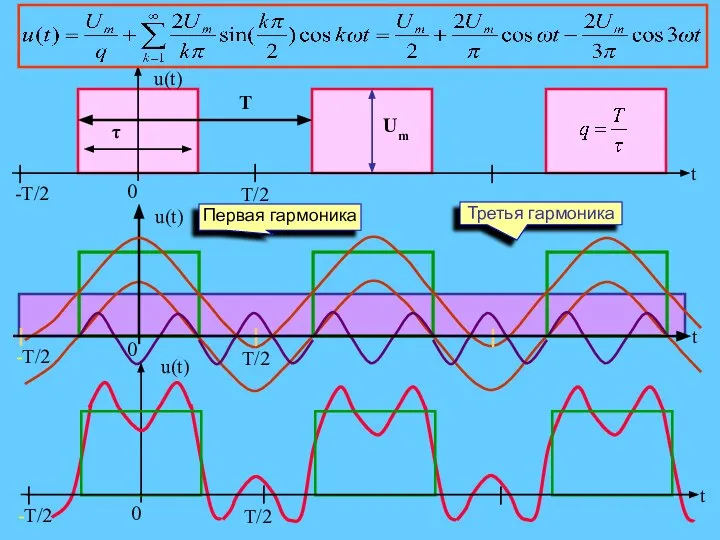
- 16. T/2 -T/2 u(t) Первая гармоника Третья гармоника
- 17. Примеры определения спектра импульсной последовательности
- 20. Особенности спектрального состава импульсной последовательности Ширина каждого лепестка равна (2π⁄τИ) и определяется только длительностью импульса. Расстояние
- 21. 3. Определение действующих значений несинусоидальных энергетических величин Определение: Действующим называют значение несинусоидального тока, эквивалентное постоянному току
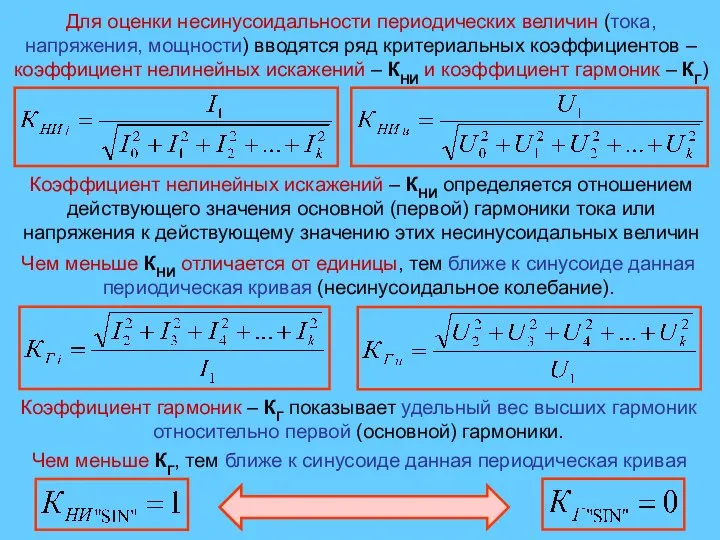
- 22. Для оценки несинусоидальности периодических величин (тока, напряжения, мощности) вводятся ряд критериальных коэффициентов – коэффициент нелинейных искажений
- 23. Мощность в электрических цепях несинусоидального тока Под активной мощностью Р несинусоидального тока понимают среднее значение мгновенной
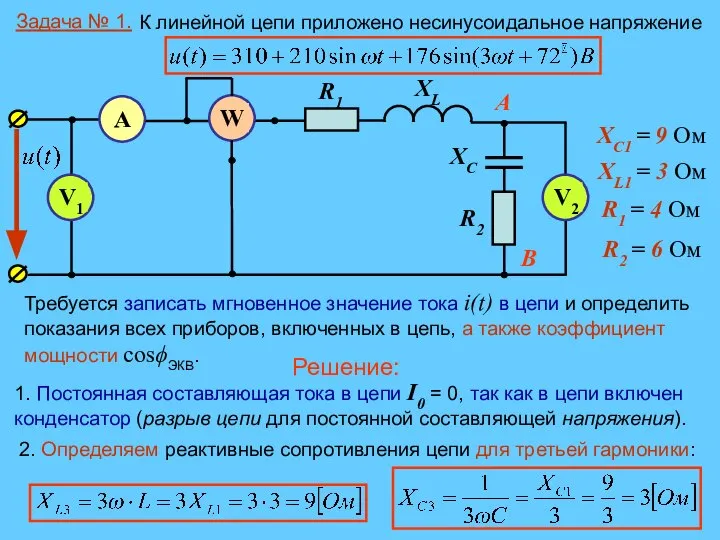
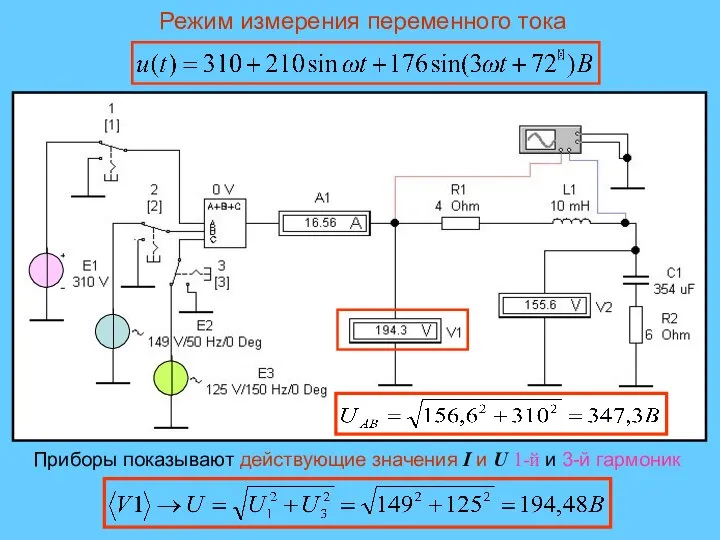
- 24. Требуется записать мгновенное значение тока i(t) в цепи и определить показания всех приборов, включенных в цепь,
- 25. 3. Полные (модули) сопротивления цепи для первой и третьей гармоник: 4. Амплитуды токов первой и третьей
- 26. 7. Вольтметр V1, подключенный ко входу цепи будет показывать действующее значение приложенного к цепи входного напряжения
- 27. 9. На участке АВ падение напряжения для 1-й и 3-й гармоник составит 10. Так как постоянная
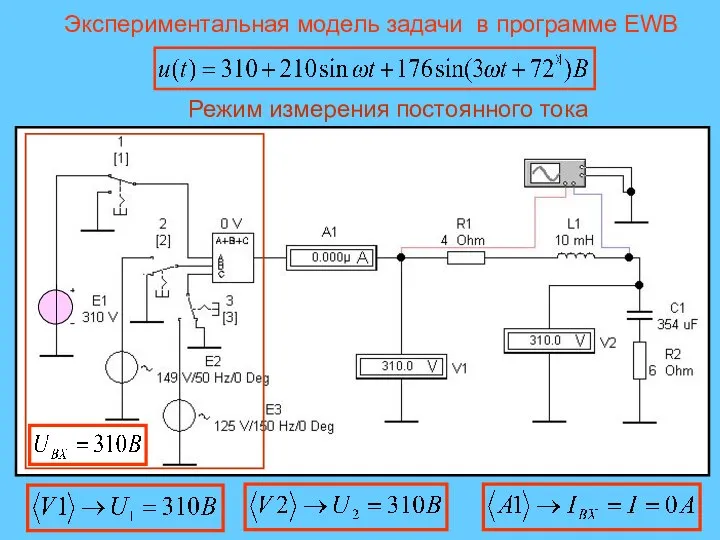
- 28. Экспериментальная модель задачи в программе EWB Режим измерения постоянного тока
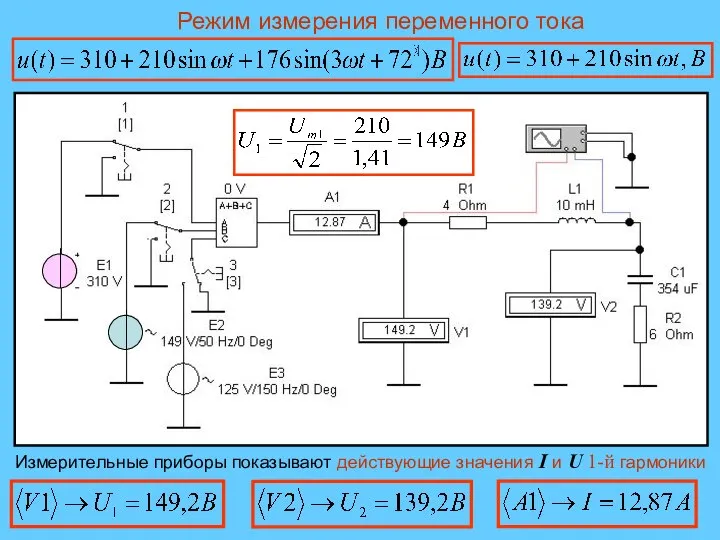
- 29. Режим измерения переменного тока Измерительные приборы показывают действующие значения I и U 1-й гармоники
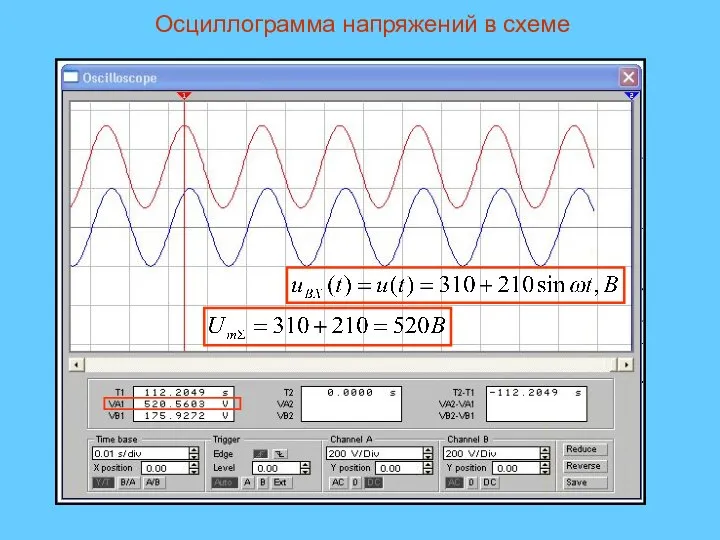
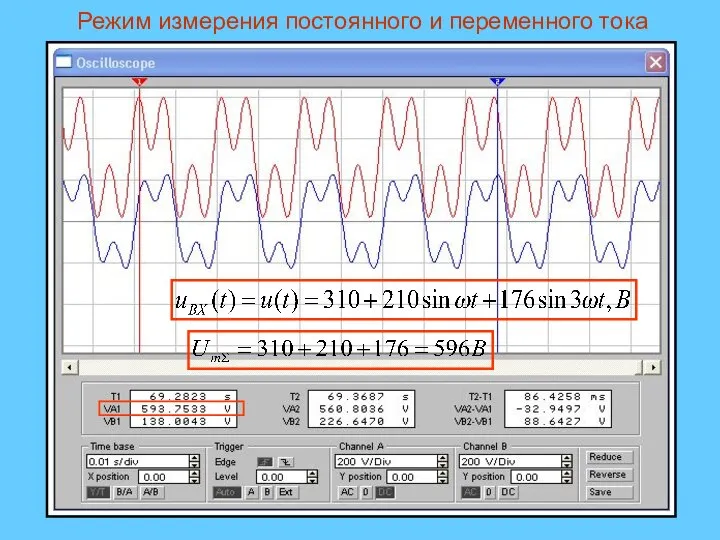
- 30. Осциллограмма напряжений в схеме
- 31. Режим измерения переменного тока Приборы показывают действующие значения I и U 1-й и 3-й гармоник
- 32. Режим измерения постоянного и переменного тока
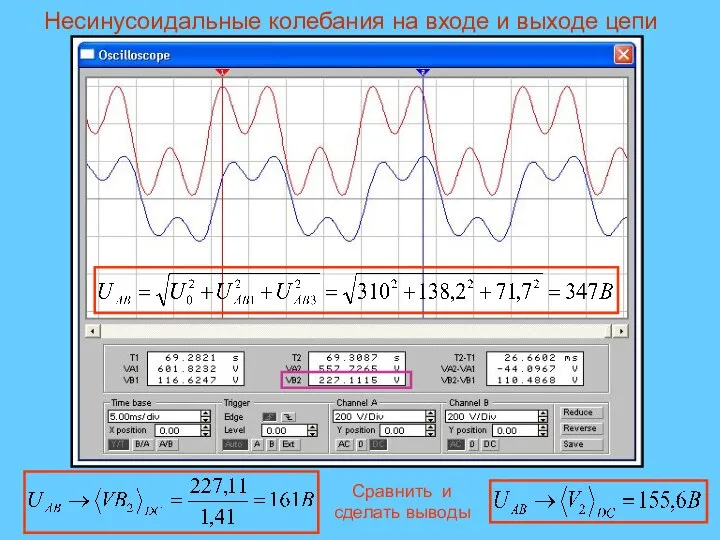
- 33. Несинусоидальные колебания на входе и выходе цепи Сравнить и сделать выводы
- 35. Скачать презентацию













 Аватария
Аватария Двумерные массивы. Таблицы (урок 6)
Двумерные массивы. Таблицы (урок 6) Управление производительностью труда на предприятии
Управление производительностью труда на предприятии СОБСТВЕННОСТЬ И ЕЕ ФОРМЫ
СОБСТВЕННОСТЬ И ЕЕ ФОРМЫ Грамматика языка
Грамматика языка Турбомашиналардың желіде бірге жұмыс істеуі
Турбомашиналардың желіде бірге жұмыс істеуі Оборотные средства предприятия
Оборотные средства предприятия Тестовые артефакты
Тестовые артефакты Что такое время
Что такое время Проблема адаптации учащихся младших классов - презентация для начальной школы_
Проблема адаптации учащихся младших классов - презентация для начальной школы_ Лекции от 12.09.2019
Лекции от 12.09.2019 Презентация "Взаимосвязь двух видов искусств" - скачать презентации по МХК
Презентация "Взаимосвязь двух видов искусств" - скачать презентации по МХК Лекция № 2. Зарождение рациональной медицины
Лекция № 2. Зарождение рациональной медицины Т-130 Бульдозері
Т-130 Бульдозері Организация, планирование и управление железнодорожным строительством. Методы ведения работ в строительстве
Организация, планирование и управление железнодорожным строительством. Методы ведения работ в строительстве Генератори. Види генераторів
Генератори. Види генераторів Заработать в Фаберлик
Заработать в Фаберлик Схема движения тепловоза 2М62
Схема движения тепловоза 2М62 Изменение структури импорта газу Давлатзода П.С Группа т-093
Изменение структури импорта газу Давлатзода П.С Группа т-093  Синтаксис цикла for. Схема работы цикла for
Синтаксис цикла for. Схема работы цикла for Гемоглобин
Гемоглобин  Презентация Государственные органы, участвующие в установлении и обеспечении ЛРР
Презентация Государственные органы, участвующие в установлении и обеспечении ЛРР  Презентация на тему "Сурдопедагогика. Кривощёкова Н.И. Интегрированный урок ''Математика-развитие речи-окружающий мир'�
Презентация на тему "Сурдопедагогика. Кривощёкова Н.И. Интегрированный урок ''Математика-развитие речи-окружающий мир'� Правоприменительная практика контрольной деятельности в сфере закупок Департамента экономического развития Курганской области
Правоприменительная практика контрольной деятельности в сфере закупок Департамента экономического развития Курганской области Презентация "Китайский театр" - скачать презентации по МХК
Презентация "Китайский театр" - скачать презентации по МХК Разработка и принятие Уголовного кодекса 1922 г.
Разработка и принятие Уголовного кодекса 1922 г. Презентация Принципы социального обслуживания в РФ и За рубежом
Презентация Принципы социального обслуживания в РФ и За рубежом  Святые земли Тотемской
Святые земли Тотемской