Формулы (1.12) и (1.13) можно называть парой преобразований Фурье.
Вторая из них
позволяет найти спектр, т. е. совокупность гармонических
составляющих, образующих в сумме s(t); первая – вычислить s(t), если
заданы гармонические составляющие (гармоники)
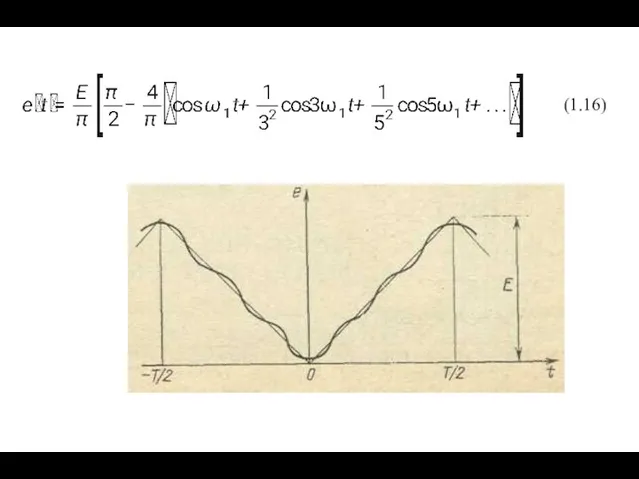
Формулу (1.12) можно представить в другом виде
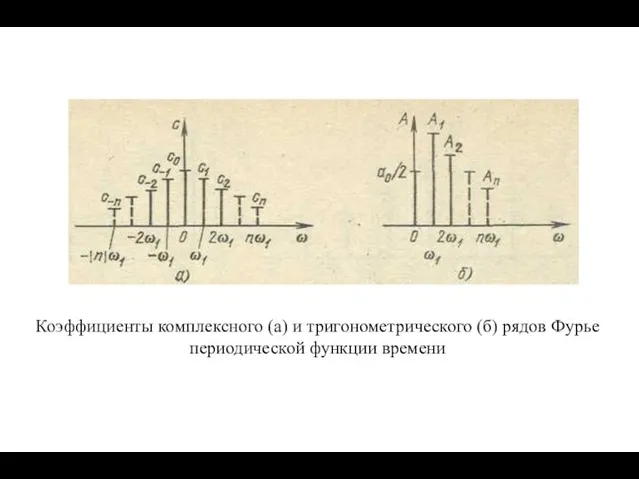
Две характеристики – амплитудная и фазовая, т. е. модули и аргументы
комплексных коэффициентов ряда Фурье, полностью определяют структуру
частотного спектра периодического колебания.
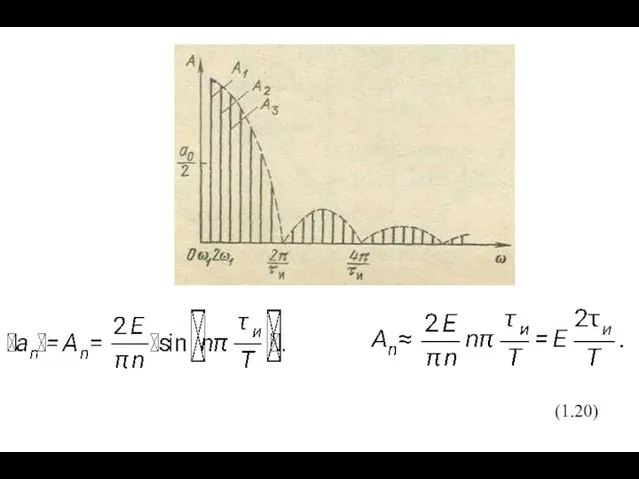
Спектр периодической функции называется линейчатым или дискретным,
так как состоит из отдельных линий, соответствующих дискретным частотам
0, ω1, 2ω1, 3ω1 и т. д.
(1.12а)












 Общие правила выполнения чертежей
Общие правила выполнения чертежей Технология цифрового телевидения
Технология цифрового телевидения ПУТЕШЕСТВИЕ ПО СТРАНЕ ПРОФЕССИОНАЛИЯ
ПУТЕШЕСТВИЕ ПО СТРАНЕ ПРОФЕССИОНАЛИЯ  Конструкторы.Деструктор
Конструкторы.Деструктор  Проектирование программных систем
Проектирование программных систем Бизнес-план
Бизнес-план Центральная регуляция стресс
Центральная регуляция стресс  С чем работаем? Полноценный мониторинг соц.медиа в рунете: Все самые популярные сервисы 1.Все самые популярные соц.сервисы 2.Монитор
С чем работаем? Полноценный мониторинг соц.медиа в рунете: Все самые популярные сервисы 1.Все самые популярные соц.сервисы 2.Монитор Бібліотека ВНЗ у веб-просторі
Бібліотека ВНЗ у веб-просторі Лекарственные растения.
Лекарственные растения. Символы в китайском искусстве. Китайский гороскоп.
Символы в китайском искусстве. Китайский гороскоп. Симметрия решетки
Симметрия решетки Форма государственного устройства
Форма государственного устройства Дизайн-проект и его реализация
Дизайн-проект и его реализация Чемпионат и мир
Чемпионат и мир Основные термины и определения рис. Графические символы мехатроники
Основные термины и определения рис. Графические символы мехатроники Замок Нидзё
Замок Нидзё Математика в архитектуре Древней Греции и средних веков. Ученик 9 а Рыбалкин Илья Руководитель: Рог
Математика в архитектуре Древней Греции и средних веков. Ученик 9 а Рыбалкин Илья Руководитель: Рог Умницы и умники ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА
Умницы и умники ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА Уравнение движения электропривода и его анализ. Приведение моментов к оси вращения вала электродвигателя. Лекция 3
Уравнение движения электропривода и его анализ. Приведение моментов к оси вращения вала электродвигателя. Лекция 3 Языкознание как комплексная гуманитарная дисциплина. Языкознание, или лингвистика
Языкознание как комплексная гуманитарная дисциплина. Языкознание, или лингвистика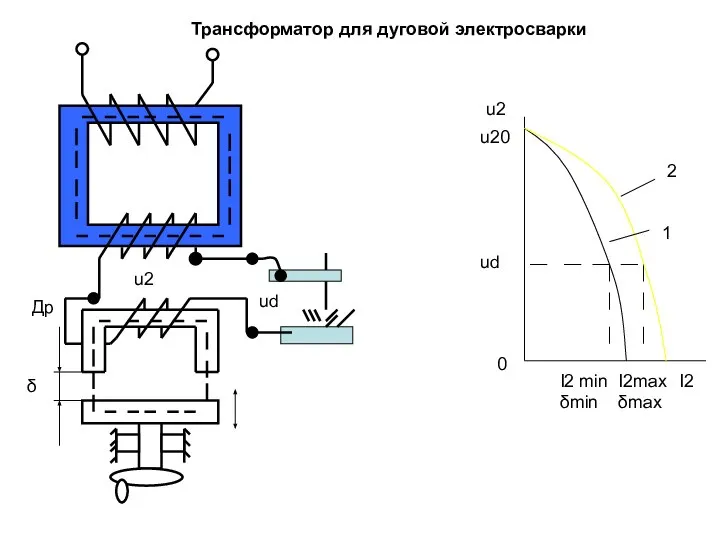 Трансформатор для дуговой электросварки
Трансформатор для дуговой электросварки  Использование современных технологий для проведения мониторинга физического состояния спортсменов и лиц, не занимающихся спорто
Использование современных технологий для проведения мониторинга физического состояния спортсменов и лиц, не занимающихся спорто Оценка деятельности Специалиста на фондовом рынке СПВБ
Оценка деятельности Специалиста на фондовом рынке СПВБ Свадебная атрибутика славян
Свадебная атрибутика славян Цифрові технології в мікроелектроніці
Цифрові технології в мікроелектроніці Причины и виды безработицы Экономические проблемы безработицы
Причины и виды безработицы Экономические проблемы безработицы Классификация зданий. Требования, предъявляемые к зданиям
Классификация зданий. Требования, предъявляемые к зданиям