Содержание
- 2. Содержание Текущий контроль Часть 1. Общие положения теории игр и их классификация. Часть 2. Примеры игр.
- 3. Текущий контроль Прогнозировать результаты голосования с помощью дерева вариантов, если число голосов каждой коалиции определяется номером
- 4. Часть 1 Общие положения теории игр и их классификация
- 5. Основные компоненты любой игры конфликт; принятие решения; оптимальность решения.
- 6. Характеризующие игру элементы чередование либо одновременность ходов, которые могут быть, как логичными, так и случайными; возможная
- 7. Классификация игр Матричные и позиционные; Антагонистические и неантагонистические; С полной и неполной информацией; Игры двух и
- 8. Часть 2 Примеры игр
- 9. Антагонистические и неантагонистические игры Антагонистическая игра: матричная игра с полной информацией и нулевой суммой Неантагонистическая игра:
- 10. Теорема о предательстве Игрок вступивший в коалицию и нарушивший ее рискует проиграть все.
- 11. Дилемма заключенного Каждому из двух заключенных, обвиняемых в одном преступлении, предлагается на выбор три альтернативы: Признать
- 12. Матричные антагонистические игры двух лиц с нулевой суммой и полной информацией Игра определяется матрицей М, строки
- 13. Часть 3 Эквивалентные преобразования игр
- 14. Доминирующая и доминируемая стратегии Стратегии i и j называются соответственно доминирующей и доминируемой, если каждый элемент
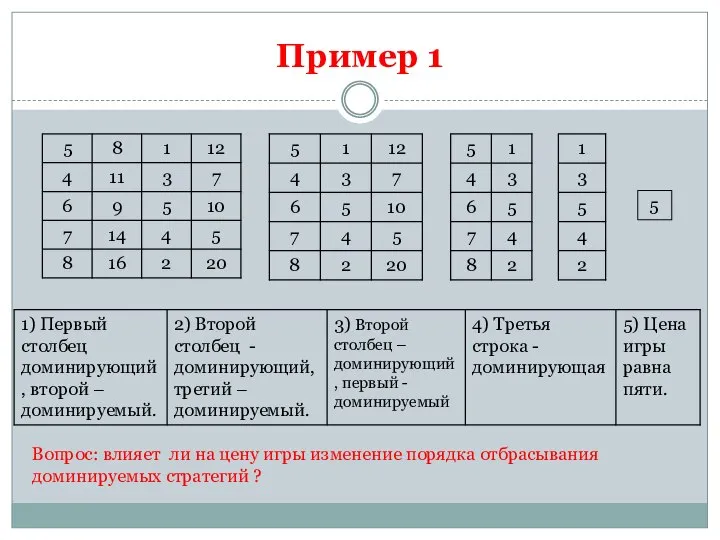
- 15. Пример 1 5 Вопрос: влияет ли на цену игры изменение порядка отбрасывания доминируемых стратегий ?
- 16. Самостоятельно Отбросить доминируемые стратегии в игре, заданной матрицей М: М =
- 17. Часть 4 Поиск решения игры в чистых стратегиях
- 18. Равновесные стратегии Ситуация (пара стратегий) называется равновесной, если соответствующий ей элемент матрицы игры является одновременно наибольшим
- 19. Пример 2 - Седловая точка
- 20. Самостоятельно Определить оптимальную стратегию преподавателя, определяемую седловой точкой в антагонистической игре двух лиц, заданной матрицей М
- 21. Гарантирующие стратегии Гарантирующие стратегии применяются в играх с полной информацией, когда отсутствует седловая точка. Применительно к
- 22. Пример 3 Желтым цветом выделены гарантирующие стратегии игроков. Цена игры при использовании гарантирующих стратегий равна семи
- 23. Самостоятельно Формально определить гарантирующие стратегии игроков. Чем гарантирующие стратегии отличаются от равновесных? Определить гарантирующие стратегии игроков
- 24. Часть 5 Поиск решения игры в смешанных стратегиях
- 25. Смешанные стратегии Игры с полной информацией, т.е. такие, в которых каждый игрок знает возможности и “наклонности”
- 26. Формальная постановка задачи поиска оптимальной смешанной стратегии Пусть - вероятность выбора i –ой стратегии одним игроком,
- 27. Теорема о минимаксе Справедлива теорема о минимаксе, в некотором смысле аналогичная теореме о седловой точке для
- 28. Метод Брауна-Робинсона Идея метода заключается в том, что игра разыгрывается много раз, причем при каждом разыгрывании
- 29. Алгоритм Брауна-Робинсона Шаг 1. Ввод матрицы игры «а» и точности Ɛ. Шаг 2. Шаг 3. Шаг
- 30. Алгоритм Брауна-Робинсона (продолжение) Шаг 8. ха=ха+1. Шаг 9. yв=yв+1. Шаг 10. Вычисляется новая цена игры V1
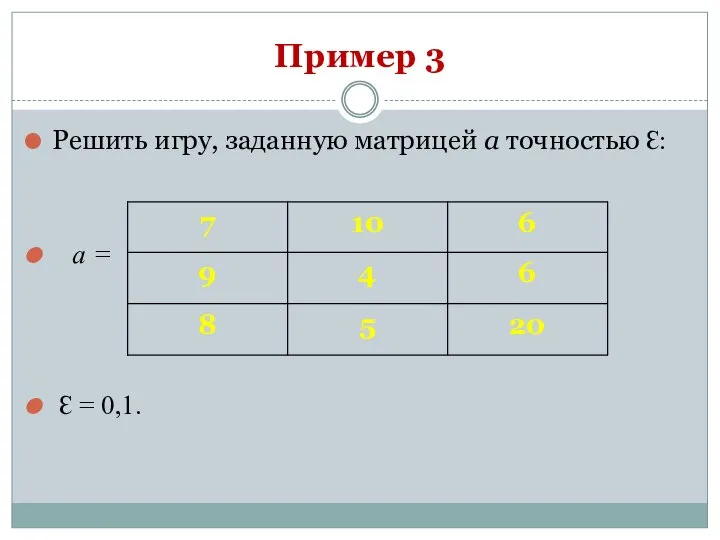
- 31. Пример 3 Решить игру, заданную матрицей а точностью Ɛ: а = Ɛ = 0,1.
- 32. Решение 1. 2. 3. V₀ =8,33(3) . 4. D = 33, A = 3. 5. C
- 34. Скачать презентацию





























 Роль интеграции предметов гуманитарного цикла в повышении качества образования.
Роль интеграции предметов гуманитарного цикла в повышении качества образования. Проект системы освещения жилого дома
Проект системы освещения жилого дома Презентация "Сравнение банков" - скачать презентации по Экономике
Презентация "Сравнение банков" - скачать презентации по Экономике Развитие устной речи у учащихся на основе аутентичного художественного фильма. Учитель:Ермакова Н.В.
Развитие устной речи у учащихся на основе аутентичного художественного фильма. Учитель:Ермакова Н.В. Физическая активность и здоровье
Физическая активность и здоровье Презентация "Основные подходы к построению математических моделей систем" - скачать презентации по Экономике
Презентация "Основные подходы к построению математических моделей систем" - скачать презентации по Экономике Биологическое окисление
Биологическое окисление  Основы программирования. Цикл for
Основы программирования. Цикл for Организация многофункционального пространства. Московский район
Организация многофункционального пространства. Московский район Гаагские конвенции 1899 и 1907 годов: эволюция международного гуманитарного права на случай войны. (анализ документов)
Гаагские конвенции 1899 и 1907 годов: эволюция международного гуманитарного права на случай войны. (анализ документов) Строительная компания TajiCK
Строительная компания TajiCK Все умеют рисовать! Рисуем с помощью ладошки.
Все умеют рисовать! Рисуем с помощью ладошки.  Рулевое управление
Рулевое управление Полупроводниковые диоды
Полупроводниковые диоды Как ухаживать за собаками и кошками? Как ухаживать за собаками и кошками? Учитель начальных классов МОУСОШ №4 города Тулы Климов
Как ухаживать за собаками и кошками? Как ухаживать за собаками и кошками? Учитель начальных классов МОУСОШ №4 города Тулы Климов Культура в меняющемся мире Изобразительное искусство Архитектура
Культура в меняющемся мире Изобразительное искусство Архитектура Презентация "Искусство. Виды искусства" - скачать презентации по МХК
Презентация "Искусство. Виды искусства" - скачать презентации по МХК Тормозная рычажная передача электровоза ВЛ 80
Тормозная рычажная передача электровоза ВЛ 80 Интернет-технологии
Интернет-технологии Информационные технологии в менеджменте. (Лекция 1)
Информационные технологии в менеджменте. (Лекция 1) Глухие и звонкие парные согласные в корне слова Белова Оксана Юрьевна, учитель начальных классов, МОУ СОШ №6 г. Реутова Московско
Глухие и звонкие парные согласные в корне слова Белова Оксана Юрьевна, учитель начальных классов, МОУ СОШ №6 г. Реутова Московско Теорема Пойнтинга
Теорема Пойнтинга Лекция 9. Ислам
Лекция 9. Ислам Комплексный эколого-краеведческий проект «Создание пеше-водного маршрута «Вниз по речке Василевке в сказку озера Сапшо»
Комплексный эколого-краеведческий проект «Создание пеше-водного маршрута «Вниз по речке Василевке в сказку озера Сапшо» Виды кабелей для компьютеров. Разъёмы
Виды кабелей для компьютеров. Разъёмы Błogosławiony Edmund Bojanowski
Błogosławiony Edmund Bojanowski Презентация Safe Case
Презентация Safe Case Репродукции художника Ряннеля Т.В
Репродукции художника Ряннеля Т.В