Содержание
- 2. Теория игр Неопределенными могут быть не только условия, в которых работает предприятие и принимаются решения, но
- 3. Теория игр ЛПР приходится считаться не только со своими собственными целями, но и с теми целями,
- 4. Теория игр Теория принятия решений в условиях конфликта или математическая теория конфликтных ситуаций
- 5. Физическая и социальная природа конфликта юридические лица, воюющие стороны, спортивные команды, конкурирующие фирмы, биологические виды в
- 6. Задача теории игр выработка рекомендаций по рациональному образу действий участников конфликта
- 7. Конфликтная ситуация Чтобы сделать возможным математический анализ ситуации, надо построить упрощенную, схематизированную модель ситуации. Такую модель
- 8. Игра – это модель конфликта Принятие решений во взаимосвязанных ситуациях: большинство проблем в экономических и социальных
- 9. Конфликт Любое явление, применительно к которому имеет смысл говорить о том, кто и как в этом
- 10. Элементы игры I - множество игроков Kd ⊂ I – коалиции действий, xi ∈ Ωi S=(x1,x2,…,xn)
- 11. Элементы игры Коалиции интересов - КI ⊂ I Заинтересованность fK(А) – каждая из коалиций предпочитает одни
- 12. Классификация игр 1) KI≥2 – не менее 2-х заинтересованных сторон 2) Kd=1 – игра нестратегическая (неопределенности
- 13. Классификация игр по количеству игроков - игры 2 и n игроков по количеству стратегий – конечные
- 14. Классификация игр Антагонистическая игра – игра двух лиц с нулевой суммой. Матричная игра – конечная игра
- 15. Матричные игры I={I,II} I: X={xi}m II: Y={yj}n f1(x,y) – функция выигрыша первого игрока f2(x,y) – функция
- 16. Матричные игры Матрица игры:
- 17. Функция выигрыша f1(xi,yj) – результат 1-го игрока, когда он сделал ход xi, а 2-ой игрок –
- 18. В антагонистической игре цели игроков противоположны: Цель первого игрока – выиграть как можно больше, цель второго
- 19. Решить игру Найти оптимальные стратегии каждого игрока и оценить результат, т.е. выигрыш первого игрока
- 20. Пример (х1,y2)→(x2,y2) (x2,y2) – ситуация равновесия Х1 Х2 Х3 y1 y2 y3
- 21. Ситуация равновесия Если один игрок придерживается стратегии, соответствующей ситуации равновесия, то второму игроку невыгодно отступать от
- 22. Ситуация равновесия Пусть (x*,y*) – ситуация равновесия f1(x,y) - выигрыш 1-го игрока f2(x,y) - выигрыш 2-го
- 23. Ситуация равновесия f1(x,y*) ≤ f1(x*,y*) f2(x*,y) ≤ f2(x*,y*) , *(-1): -f2(x*,y) ≥ -f2(x*,y*), но f1(x,y) =
- 24. Ситуация равновесия Точка, выигрыш в которой первого игрока минимален по y и максимален по x:
- 25. Гарантированный результат ν1= maxx miny fij – гарантированный результат 1-го игрока
- 26. Гарантированный результат ν2= min max fij - y x гарантированный результат 2-го игрока 5 2 4
- 27. Гарантированные результаты ν1=ν – нижняя цена игры, ν2= – верхняя цена игры
- 28. Th. Неравенство минимаксов ν ≤ , или ≤
- 29. Доказательство ≤ - по свойству с.р. Но если f(x) то min f(x)
- 30. Неравенство минимаксов Если функция ограничена сверху константой, то и максимум этой функции ограничен ею же ч.т.д.
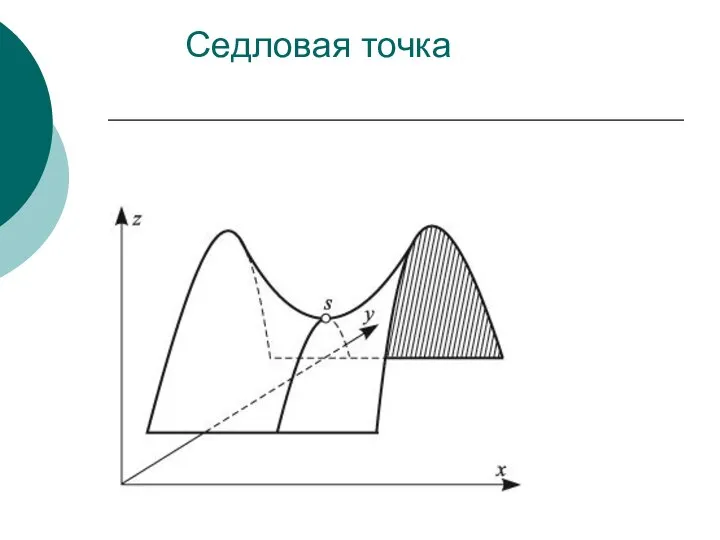
- 31. Ситуация равновесия ν1= maxx miny fij ν2= miny maxx fij Если ν1= ν2 - седловая точка
- 32. Седловая точка
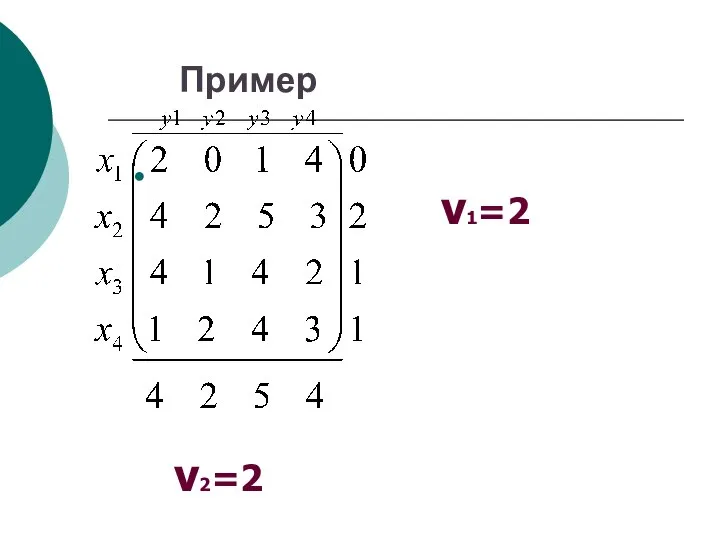
- 33. Пример ν1=2 ν2=2
- 34. Седловая точка Седловых точек в игре может быть несколько, причем цена игры в каждой одинакова
- 35. Принцип достижимости целей Стремление игроков к ситуации равновесия, описываемой седловой точкой, т.к. только ситуации равновесия могут
- 36. Существуют ли оптимальные решения в играх без седловых точек? Теорема Неймана гарантирует, что каждая антагонистическая игра
- 37. Пример 6 8 __________________ 2 4 = 4; =6. ν∈ [4;6] ν – цена игры
- 38. Игры с закрытой информацией В играх без седловой точки свои ходы надо тщательно скрывать. Однако интервал
- 39. Идея использования смешанных стратегий Правильное поведение состоит в том, чтобы стратегию выбирать случайно – не на
- 40. Смешанная стратегия Случайная величина, значениями которой являются чистые стратегии игрока. Это сложная стратегия, состоящая в случайном
- 41. Смешанная стратегия Р= - смешанная стратегия первого игрока, или вероятностное распределение на множестве чистых стратегий Р
- 42. Смешанная стратегия Q= - cмешанная стратегия второго игрока, Q = (q1, q2, …, qn), ∑ qj=1.
- 43. Смешанная стратегия Применение смешанной стратегии - это гибкая тактика, при которой противник не знает и не
- 44. Смешанная стратегия Любая чистая стратегия является частным случаем смешанной: например, х1=Р(1,0,…,0). Таким образом, для любой игры
- 45. Алгоритм решения игры Упростить игру. Найти гарантированные результаты для каждого игрока. Если существует седловая точка, то
- 46. Решение игр 2х2 А= - платежная матрица Решение игры будем искать в смешанных стратегиях: P=(p1,p2) -
- 47. Решение игр 2х2 Это значит, что первый игрок будет применять свою первую стратегию х1 с вероятностью
- 48. Пример P1 p2 q1 q2 Мν=6p1q1+2p1q2+4p2q1+8p2q2 p2=1-p1, q2=1-q1 Мν= 6p1q1+2p1(1-q1)+4(1-p1)q1+8(1-p1)(1-q1)= ν∈ [4;6]
- 49. =-6p1-4q1+8+8p1q1= =8(p1-1/2)(q1-3/4)+5 Ответ: P={1/2; 1/2}; Q={3/4; 1/4}; ν=5
- 50. Решение игр 2х2 Решим игру в общем виде с точки зрения второго игрока Перепишем матрицу игры
- 51. Решение игр 2х2 (а11-а21)⋅q1+(a12-а22)⋅q2=0, затем, учитывая, что q2=1-q1, получим (а11-а21-а12+а22)⋅q1+(a12-а22)=0. Отсюда q1=-(a12-а22)/(а11-а21-а12+а22). Подставляя это значение q1
- 52. С точки зрения первого игрока а11⋅p1+a21⋅p2=ν - при первой стратегии второго игрока, а12⋅p1+a22⋅p2=ν - при второй
- 53. Пример Матрица игры А= Составим систему уравнений для второго игрока: 6q1+2q2=ν 4q1+8q2=ν решая совместно, получим 2q1-6(1-q1)=0,
- 54. Пример Найдем оптимальную стратегию первого игрока. Поскольку цена игры уже известна, то достаточно написать только одно
- 55. Ответ: P=(1/2;1/2), Q=(3/4;1/4), ν =5.
- 56. Решение примера методом Крамера А= , ее определитель ⏐А⏐=6⋅8-4⋅2=40. Тогда q1= , q2= Поскольку q1+q2=1, то
- 57. Решение примера методом Крамера Вероятности P можно найти аналогично, но из транспонированной матрицы А*= , 6p1
- 58. Решение игр 2×n и m×2 Если один из игроков имеет 2 стратегии, а другой игрок -
- 59. Решение игр 2×n У первого игрока - 2 стратегии, у второго игрока - n стратегий. Если
- 60. Решение игр 2×n Матрица игры: p2=1-p1 ν1=a11 p1+a21 p2= a21+(a11-a21)p1 ν2=a12 p1+a22 p2= a22+(a12-a22)p1 …. νn=a1n
- 61. Графо-аналитический метод Линейные функции ν1, ν2,…,νn отражают зависимость среднего выигрыша 1-го игрока от вероятности р1 при
- 62. Гарантированный результат первого игрока ν= max min{a2j+(a1j – a2j)p1} i j
- 63. Чтобы обеспечить себе гарантированный результат, первый игрок должен выделить нижнюю границу среднего выигрыша при любой стратегии
- 64. Решение игры Соответствующая абсцисса равна вероятности применения первым игроком его первой стратегии, а ордината равна цене
- 65. Пример Решить игру А= =1, =3 Решаем ее с точки зрения I игрока ν1=2р1+4р2=2р1+4(1-р1)=4-2р1 ν2=3р1+р2=1+2р1 ν3=
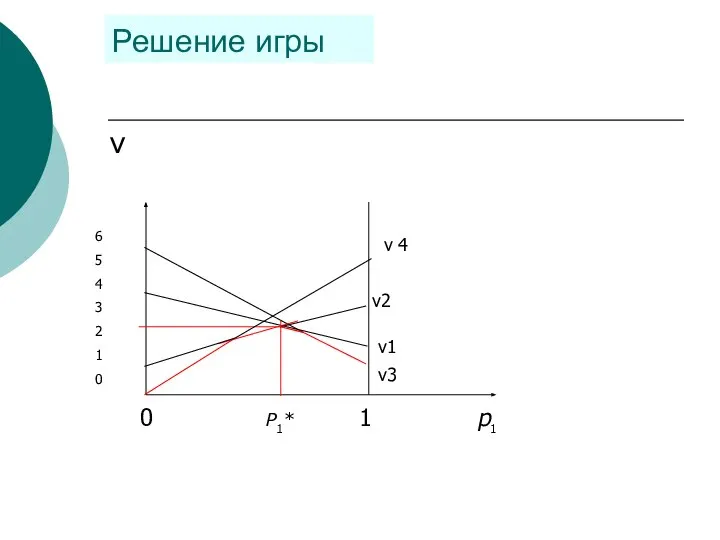
- 66. 6 5 4 3 2 1 0 ν 4 ν2 ν3 ν1 0 Р1* 1 р1
- 67. Верхняя точка границы образована пересечением прямых ν3 и ν2 (р1*, ν)∈ ν3∩ν2. Координаты точки пересечения найдем
- 68. Для 2-го игрока стратегии y1 и y4 – неактивные, т.к. не используются в смешанной стратегии. Тогда
- 69. Решение игр m×2 У 1-го игрока m стратегий, у 2-го игрока – 2 стратегии Матрица игры
- 70. Решаем с точки зрения того игрока, который имеет 2 стратегии, т.е. второго. Р= (р1,…, рm) –
- 71. Средний проигрыш 2-го игрока ν1=a11 q1+a12 q2=a11+(a11 - a12)q1 … νm=am1q1+am2q2=am1+(am1 - am2)q1 q1 q2
- 72. Гарантированный результат второго игрока
- 73. Средний проигрыш 2-го игрока В семействе прямых, описывающих средний проигрыш 2-го игрока, отмечаем верхнюю границу и
- 74. Смешанная стратегия 1-го игрока Активными стратегиями первого игрока будут те, которые соответствуют прямым, образующим точку пересечения
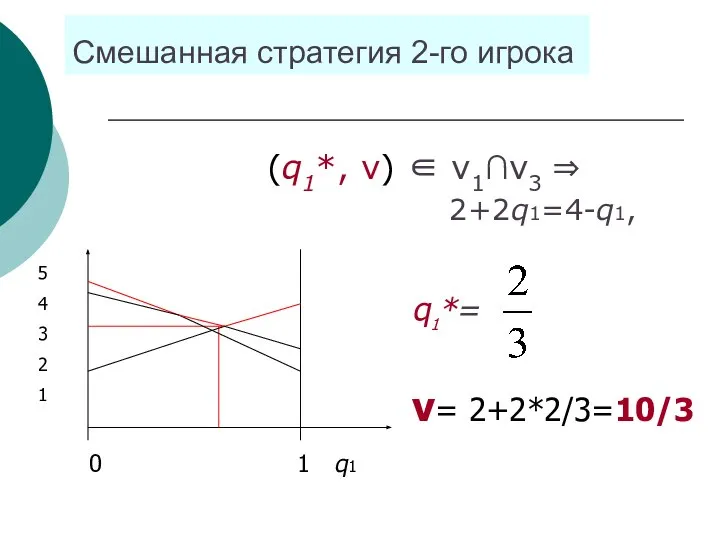
- 75. Пример Матрица игры Средний проигрыш 2-го игрока ν1=4q1+2q2 = 4q1 +2(1-q1)= 2+2q1, ν2=2 q1+5q2= 5-3q1, ν3=3q1+4q2=4-q1
- 76. Смешанная стратегия 2-го игрока (q1*, ν) ∈ ν1∩ν3 ⇒ 2+2q1=4-q1, 0 1 q1 5 4 3
- 77. Смешанная стратегия 1-го игрока Из матрицы А* p1= = = Ответ: Q=(2/3; 1/3), ν=10/3, P=(1/3; 0;
- 78. Решение игр mxn X={xi}m – стратегии 1-го игрока Y={yj}n – стратегии 2-го игрока Р=(р1, р2, …,
- 79. Первый игрок Найдем сначала оптимальную стратегию Р. Она должна обеспечить выигрыш ≥ν при любой стратегии противника
- 80. Пусть ν>0 Чтобы это выполнялось, достаточно, чтобы все элементы матрицы aij >0. В противном случае можно
- 81. для любого j Введем обозначения: xi=pi/ν, тогда Выбор должен быть максимально возможным, следовательно, 1/ν принимает минимальное
- 82. Второй игрок Все аналогично решению игры для первого игрока, только второй игрок стремится не максимизировать, а
- 83. для любого i. для любого i. Заменим yj=qj/ν, тогда Σyj=1/ν Требуется так выбрать переменные yj, чтобы
- 84. Симметричные игры Опр. Квадратная матрица А={aij} называется кососимметричной, если aij= - aji для любого i.
- 85. Tеорема Значение симметричной игры равно нулю. Кроме того, если х – оптимальная стратегия первого игрока, то
- 86. Пример По теореме ν=0; т.к. P=Q, то найдем P. Р1 Р2 Р3
- 87. Средний выигрыш 1-го игрока -р2+2р3=0 → р2=2р3 р1 -3р3=0 → р1 =3р3 -2р1+3р2 =0 р1+ р2+
- 88. Метод итераций Брауна-Джонсона Разыгрывается мысленный эксперимент, в котором 1-ый и 2-ой применяют друг против друга свои
- 89. Смешанная стратегия игрока в разных случаях имеет разный смысл. Иногда конфликт должен быть разрешен всего за
- 90. Например, размещение заказа на разных предприятиях установление цены на продукцию оснащение производства современным оборудованием ведение боевых
- 91. Тактические задачи - В задачах поиска наилучших способов использования потенциала системы («тактических») оптимальные смешанные стратегии реализуются
- 92. Физическая смесь стратегий В задачах выбора рациональных параметров («технических») случайный подбор технических показателей недопустим. Физическая смесь
- 93. - создание уникальных систем; строительство капитальных сооружений; крупносерийное производство и другие долгосрочные мероприятия, требующие значительных затрат
- 94. Модель комплектации вычислительного центра Предполагается организовать ВЦ коллективного пользования, который может быть оснащен ЭВМ 4-х типов.
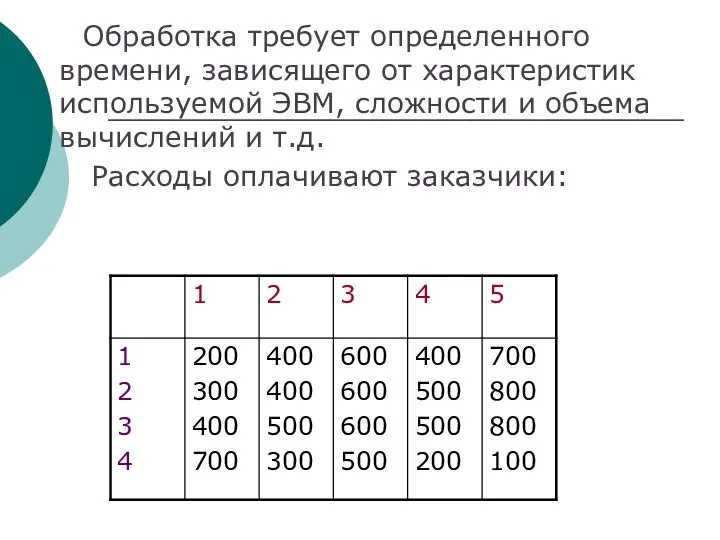
- 95. Обработка требует определенного времени, зависящего от характеристик используемой ЭВМ, сложности и объема вычислений и т.д. Расходы
- 96. Цели 1 –ый игрок (организаторы ВЦ) стремится увеличить приток средств от заказчика за счет ускорения обработки
- 97. 400р3+700р4=ν1= 700-300р3 500р3+200р4=ν4= 200+300р3 800р3+100р4=ν5= 100+700р3
- 98. Решение Р=(0; 0; 5/6; 1/6) ν=450 Количество ЭВМ оценивается с помощью методов ТМО
- 99. Замечание Антагонистические игры описывают конфликты весьма частного вида
- 100. После того, как с помощью матричной игры оценили личные стратегические возможности ЛПР (1-ый игрок) при полном
- 101. Обоснование решений с использованием биматричных игр Антагонистические игры не описывают конфликты с числом сторон >2. Интересы
- 102. Игры двух лиц с произвольной суммой (бескоалиционные) 1-ый игрок: {хi}m=Х 2-ой игрок: {yj}n=Y A={aij} – выигрыш
- 103. Решение игры С точки зрения первого игрока его средний выигрыш (матрица А) должен быть больше или
- 104. Решение игры A= Средний выигрыш первого игрока: Мν1=
- 105. ∑aij qj ≤ ∑∑aijpiqj , j i j n ∑qj=1, для любых i, j j=1 ,
- 106. Средний выигрыш второго игрока: Мν2= M m n m ∑bij pi ≤ ∑∑bijpiqj , ∑pi=1 для
- 107. Существование с.р. в бескоалиционных играх не определяет их решений Однозначные рекомендации для сторон пока отсутствуют
- 108. Пример А= В= р1= = р2= = ν1= - 4/7 Р=(1/7; 6/7).
- 109. Для 2-го игрока Матрица В содержит выигрыши 2-го игрока, цель которого – тоже выиграть как можно
- 110. A={aij}, B={bij} (A,B)={(aij,bij)} ОБОЗНАЧЕНИЯ
- 111. Редко удается предсказать исходы Б. игр Отсутствие связи между платежами сторон (нет влияния сторон друг на
- 112. В неантагонистической игре отклонение игрока от с.р. может по-разному повлиять на выигрыш другого
- 113. Теорема Нэша Каждая биматричная игра имеет по крайней мере одну ситуацию равновесия. Равновесный по Нэшу результат
- 114. Только равновесные ситуации могут быть предметом результативных переговоров Необходим анализ игры с целью установления таких ситуаций
- 115. Пример 1. Переговоры по сокращению объема продукции y1 y2 x1 x2 1 – настаивать на принятии
- 116. Пример 2. Переговоры о масштабах сокращения объема продукции Альтернативы 1 – выпуск на прежнем уровне; 2
- 117. В отсутствие контроля ни одна из сторон не пойдет на сокращение выпуска продукции
- 118. Б. Действенные меры контроля (разработана система штрафов за нарушение договоренностей) (3;3) (7;0) (0;7) (8;8) х1 х2
- 119. Ситуация Равновесия по Нэшу - схема анализа, когда никакое кооперирование не допускается. Если равновесный по Нэшу
- 120. Во многих случаях полезны и даже необходимы контакты и соглашения между участниками, поэтому модели, допускающие возможность
- 121. Кооперативная игра Разрешено заключать совместные соглашения Допускается совместный выбор стратегий Допускается передавать полезность от одного игрока
- 122. «Справедливый дележ» по Нэшу «начало отсчета» - (ν1*, ν2*) - минимальный результат, ниже которого игрок не
- 123. Мультипликативная целевая функция φ(ν1, ν2) моделирует допустимую компенсацию уменьшения одних значений частных компонентов за счет увеличения
- 124. Если кто-то из игроков не удовлетворен компромиссным решением, он может исследовать свои стратегические возможности по применению
- 125. Применение стратегии угроз (реальная или провозглашенная в качестве возможной альтернатива поведения: склонить противника к мысли, что
- 126. Эффективность стратегии угрозы определяется результатом истинного воздействия на физический объект (изменение состояния объекта) психологическим воздействием на
- 127. Пример (1;4) (-2;-4) (-3;-1) (4;1) 4 -3 -4 1 4 Пусть стратегия угроз 1-го – х2
- 128. Решение φ(ν1,ν2)=- (ν1)↑2+3ν1+18 φ’(ν1)=-2ν1+3=0 ν’1=1,5; ν’2=3,5
- 129. Теория кооперативных игр продолжает развиваться, привлекая к себе внимание исследователей прикладных проблем, в частности, проблем АСОиУ
- 131. Скачать презентацию

































![Пример 6 8 __________________ 2 4 = 4; =6. ν∈ [4;6] ν – цена игры](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1299109/slide-36.jpg)










![Пример P1 p2 q1 q2 Мν=6p1q1+2p1q2+4p2q1+8p2q2 p2=1-p1, q2=1-q1 Мν= 6p1q1+2p1(1-q1)+4(1-p1)q1+8(1-p1)(1-q1)= ν∈ [4;6]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1299109/slide-47.jpg)





















































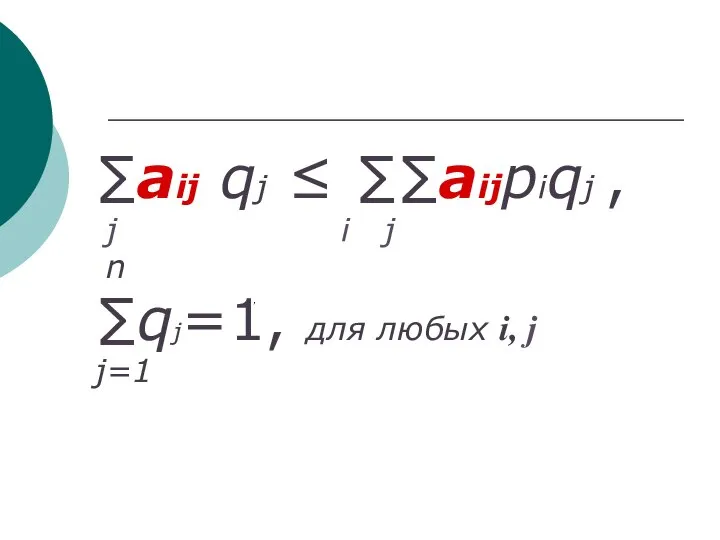




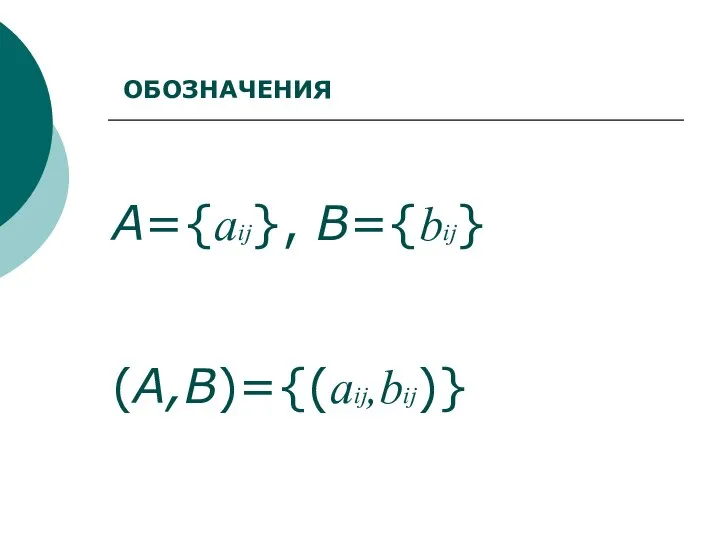


















 Тригонометрические неравенства
Тригонометрические неравенства Анализ кадровой политики ОАО «РУСАЛ-ИркАЗ»
Анализ кадровой политики ОАО «РУСАЛ-ИркАЗ» Язык программирования С++. Указатель. Массив и указатель. Арифметика для указателей
Язык программирования С++. Указатель. Массив и указатель. Арифметика для указателей Волжская Булгария
Волжская Булгария Проектная деятельность в учебном процессе Подготовила учитель химии МОУ Дубровицкая СОШ Венедиктова Г.Н.
Проектная деятельность в учебном процессе Подготовила учитель химии МОУ Дубровицкая СОШ Венедиктова Г.Н. Спуски, подъемы, торможение, подъемы на лыжах
Спуски, подъемы, торможение, подъемы на лыжах Внимание: профессиональная ошибка медицинского работника!
Внимание: профессиональная ошибка медицинского работника! Выборы. Политические партии в Англии
Выборы. Политические партии в Англии Сравнение GIMP и Photoshop
Сравнение GIMP и Photoshop Методы правового регулирования информационного права
Методы правового регулирования информационного права  Основные нормативно-правовые акты, регулирующие отношение государства к лицам с ограниченными возможностями здоровья
Основные нормативно-правовые акты, регулирующие отношение государства к лицам с ограниченными возможностями здоровья зарплата
зарплата  Гибридные двигатели
Гибридные двигатели Основные правила Web-дизайна
Основные правила Web-дизайна Статистическое наблюдение
Статистическое наблюдение Конституция-основной закон РФ
Конституция-основной закон РФ  Указатель уровня топлива
Указатель уровня топлива Анаэробный распад глюкозы Глюконеогенез
Анаэробный распад глюкозы Глюконеогенез Cybersport-bootsamp
Cybersport-bootsamp Презентация Экономическая сущность и значение материальных запасов
Презентация Экономическая сущность и значение материальных запасов Современные религиозные проблемы
Современные религиозные проблемы Производственная мощность1
Производственная мощность1 Организация пользовательского приемочного тестирования (UAT) в крупном проекте Александр Башарин. Перфоманс лаб.
Организация пользовательского приемочного тестирования (UAT) в крупном проекте Александр Башарин. Перфоманс лаб. РЕГУЛЯЦИЯ АКТИВНОСТИ ФЕРМЕНТОВ
РЕГУЛЯЦИЯ АКТИВНОСТИ ФЕРМЕНТОВ 1 сентября Визит министра образования и науки РФ ДМИТРИЯ ЛИВАНОВА
1 сентября Визит министра образования и науки РФ ДМИТРИЯ ЛИВАНОВА Презентация Правовая характеристика, виды и особенности экологической экспертизы
Презентация Правовая характеристика, виды и особенности экологической экспертизы  Информационные технологии в защите баз данных таможенных органов в свете вступления России в ВТО Студентка 2 курса Экономическо
Информационные технологии в защите баз данных таможенных органов в свете вступления России в ВТО Студентка 2 курса Экономическо Жанғыш сұйықтықтар температурасы
Жанғыш сұйықтықтар температурасы