Содержание
- 2. Пример «Строительство аэропорта» Критерии Стоимость строительства Расстояние от города Минимальное шумовое воздействие
- 3. Пример (альтернативы) А: $ 100 млн; 20 мин; 50 тыс. чел; Б: $ 130 млн; 30
- 4. МКЗ (Ω, {fi}n, {⎬,~}), где {fi}n - n целевых функций fi, каждая из которых сформулирована в
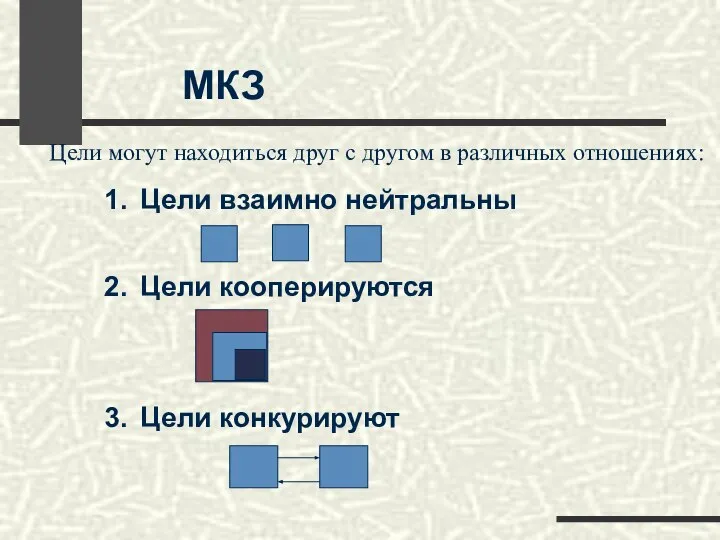
- 5. МКЗ 1. Цели взаимно нейтральны 2. Цели кооперируются 3. Цели конкурируют Цели могут находиться друг с
- 6. Цели нейтральны xЄΩ1 … xЄΩ xЄΩn-1
- 7. Алгоритм решения МКЗ уменьшить исходное множество альтернатив, убрав заведомо худшие свести задачу к однокритериальной путем введения
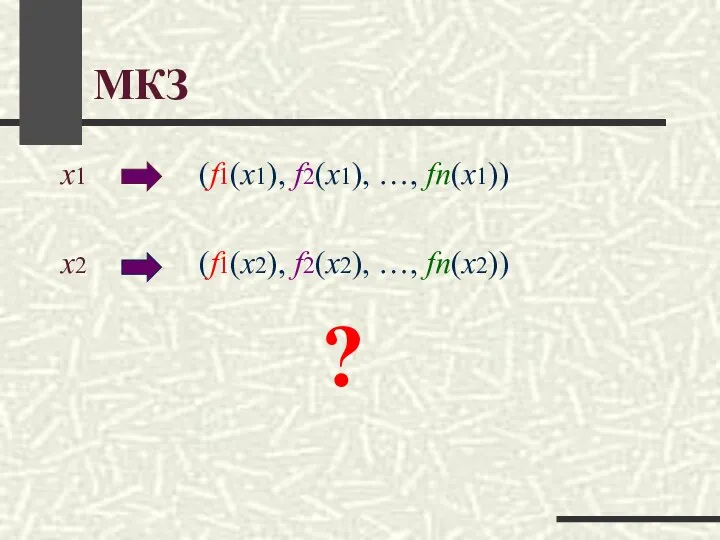
- 8. МКЗ x1 (f1(x1), f2(x1), …, fn(x1)) x2 (f1(x2), f2(x2), …, fn(x2)) ?
- 9. Принцип Парето Пусть x1 и x2 – альтернативы. Если для i fi(x1) ≥ fi(x2), причем хотя
- 10. Множество Парето Оставшиеся альтернативы образуют множество Парето - множество неулучшаемых альтернатив, или множество несравнимых альтернатив,
- 11. Множество Парето или таких, улучшение которых по одним критериям приводит к их ухудшению по другим Возможные
- 12. Критериальное пространство В критериальном пространстве альтернативы заданы точками, проекции которых на оси являются оценками альтернатив по
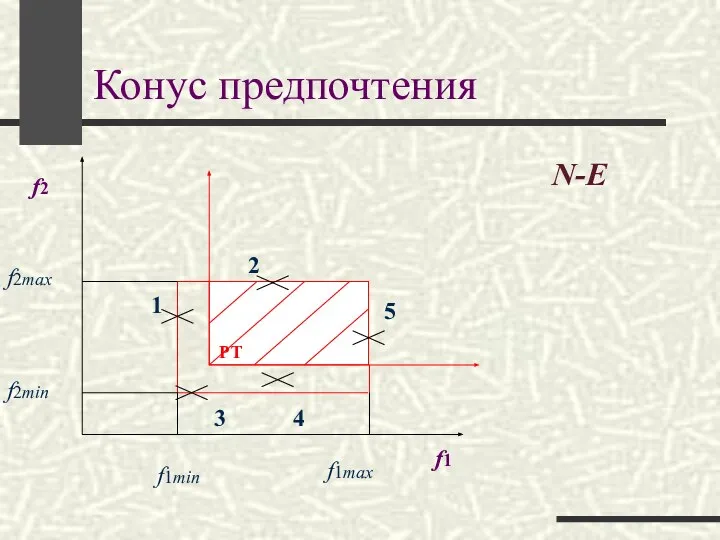
- 13. Конус предпочтения N-E f1 f2 1 2 3 4 5 РТ f2max f2min f1min f1max
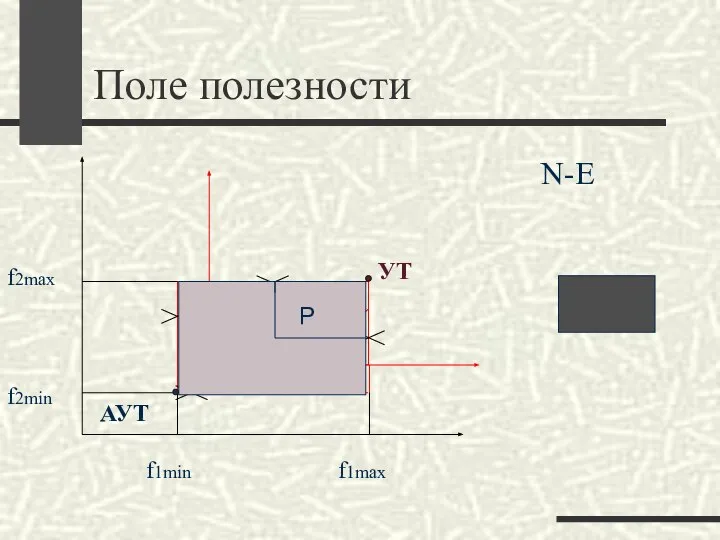
- 14. Поле полезности N-E f1max f2max f1min f2min АУТ УТ Р
- 15. Способы задания альтернатив координатный (альтернативы заданы своими координатами в критериальном пространстве) графический (альтернативы образуют непрерывное множество
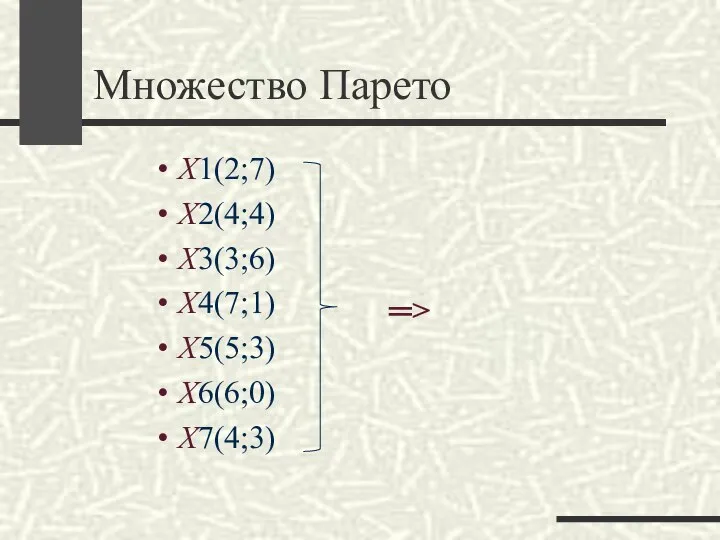
- 16. Множество Парето Х1(2;7) Х2(4;4) Х3(3;6) Х4(7;1) Х5(5;3) Х6(6;0) Х7(4;3) ═>
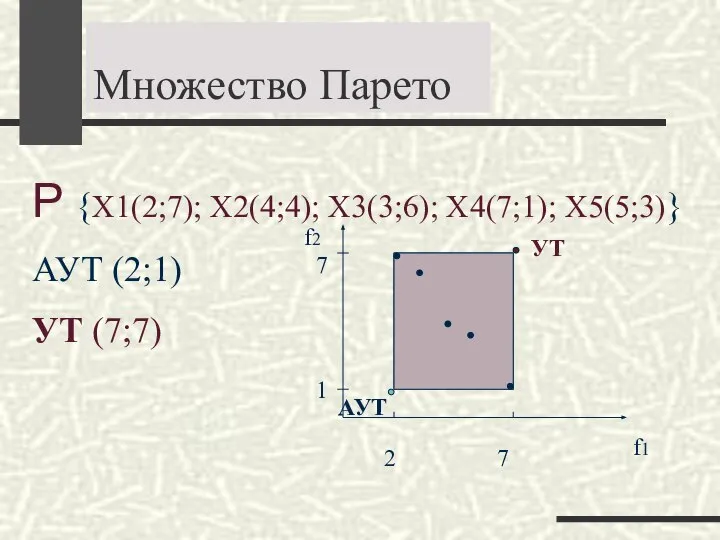
- 17. Множество Парето Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)} АУТ (2;1) УТ (7;7) 7 1 2 7
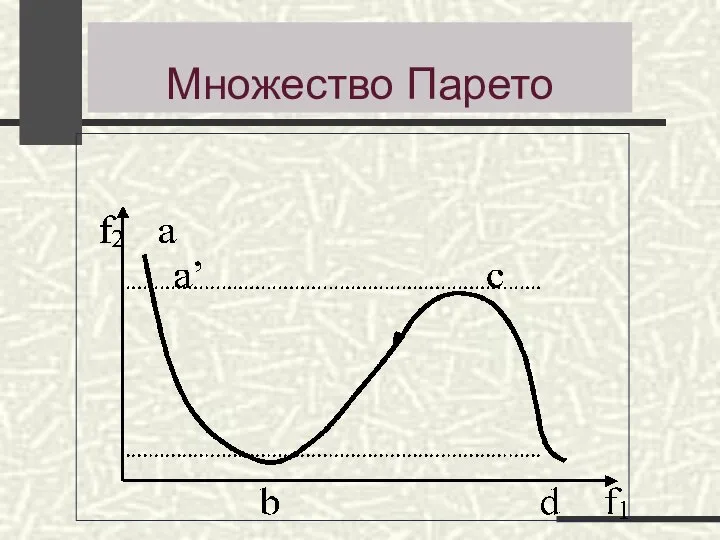
- 18. Множество Парето
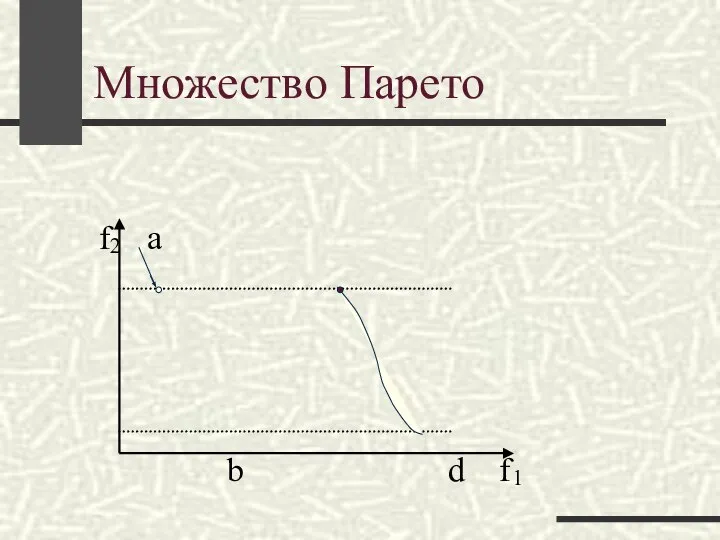
- 19. Множество Парето
- 20. Множество Парето Все альтернативы из множества Парето являются решением многокритериальной задачи в смысле этого принципа, т.е.
- 21. Перевод в однородную шкалу fi*(x) - оценка альтернативы x по i-му критерию в «родной» шкале fimax
- 22. Перевод в однородную шкалу А: $ 100 млн; 20 мин; 50 тыс. чел; Б: $ 130
- 23. Принятие решений при неопределенности целей Интегральный критерий Метод Нэша Метод контрольных показателей Простейший метод Введение метрики
- 24. Интегральный критерий x (f1(х), f2(х), …, fn (х)) F(x) Его роль – поставить в соответствие каждой
- 25. Метод арбитражных решений, или метод Нэша АУТ( ) F(x)=
- 26. Пример Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)} F(x1)=(2-2)(7-1)=0 F(x2)=(4-2)(4-1)=6 F(x3)=(3-2)(6-1)=5 F(x4)=(7-2)(1-1)=0 F(x5)=(5-2)(3-1)=6 АУТ (2;1) х2 ~
- 27. Использование контрольных показателей {fi*}n, fi (x) ≥ fi*,
- 28. Пример Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)} Пусть f1*=3; f2*=2 АУТ (2;1) F(x2)=min{4/3; 4/2}=4/3 F(x3)=min{3/3; 6/2}=1
- 29. Простейший способ Ранг, равный 1, присваивается главному критерию
- 30. Введение метрики в пространстве целевых функций УТ(fimax)
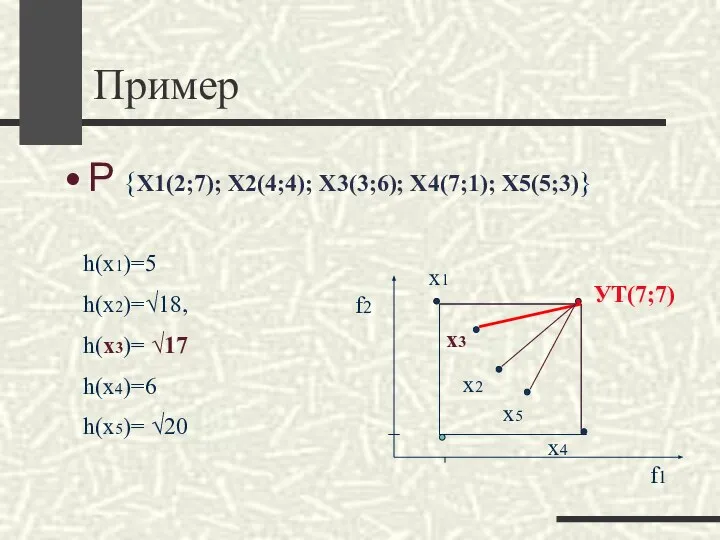
- 31. Пример Р {Х1(2;7); Х2(4;4); Х3(3;6); Х4(7;1); Х5(5;3)} h(x1)=5 h(x2)=√18, h(x3)= √17 h(x4)=6 h(x5)= √20
- 32. Пример А: $ 100 млн; 20 мин; 50 тыс. чел; Б: $ 130 млн; 30 мин;
- 33. Cвертка здесь x – альтернатива из множества Парето fi(x) – оценка альтернативы x по i-му критерию
- 34. Свертка Ci – коэффициенты относительной важности критериев
- 35. Экспертное оценивание Пусть rij – ранг, который присвоил j–ый эксперт i–му критерию Чтобы получить числовую оценку,
- 36. Экспертное оценивание Тогда коэффициент значимости i-го критерия с точки зрения j–го эксперта Ci
- 37. Экспертное оценивание Пусть gj – компетентность j–го эксперта, тогда Ci
- 38. Оценивание Th. Если , то Ci=hCj, Ci>0, ∑Ci=1 Решая систему линейных уравнений, получим искомые коэффициенты Ci
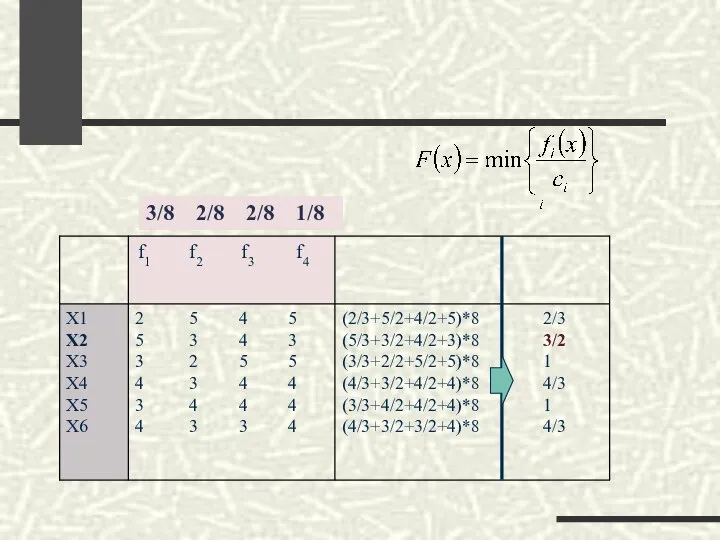
- 39. Пример , f2~ f3 , . C1=3/8; C2=2/8; C3=2/8; C4=1/8 C1=1,5C2; C2=C3; C3=2C4; C1+C2+C3+C4=1; 3/8 2/8
- 40. Использование линейной свертки Это задачи, связанные с критериями суммарного ущерба или прибыли, дохода, денежных или временных
- 41. Квадратичная свертка
- 42. Свертка порядка t Величина t, стоящая в показателе степени, отражает допустимую степень компенсации малых значений одних
- 43. недопустима никакая компенсация, и требуется выравнивание значений всех критериев (равномерное «подтягивание» значений всех критериев к их
- 44. 3/8 2/8 2/8 1/8
- 45. t→0 - мультипликативная функция требуется обеспечение примерно одинаковых уровней значений отдельных частных критериев
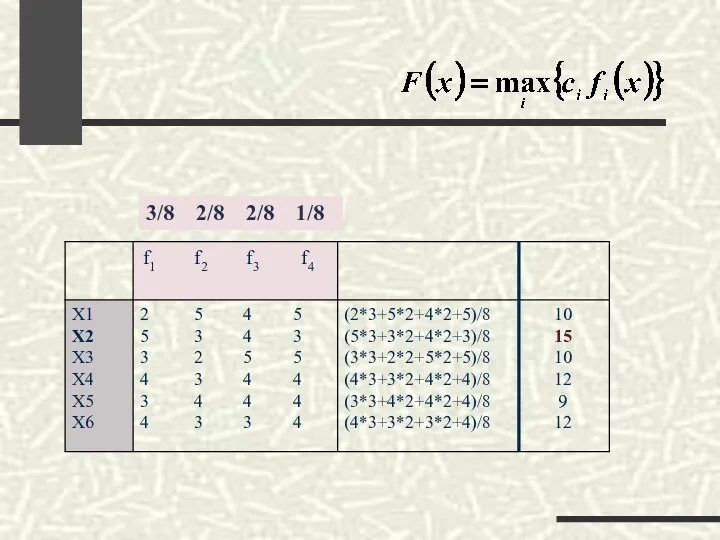
- 46. В задачах планирования ударов «по узкому месту» допустима компенсация увеличения одного из критериев сколь угодно большим
- 47. 3/8 2/8 2/8 1/8
- 48. Свертка Используя в качестве интегрального критерия свертку, выбирают в качестве лучшей ту альтернативу, для которой F(x)
- 49. Multi-Attribute Utility Theory (MAUT) Используется при возможном структурировании системы целей, представлении ее в виде иерархии. Идея
- 50. Алгоритм MAUT Оценивается частичная полезность каждой альтернативы по отношению к соответствующему критерию Оцениваются коэффициенты относительной важности
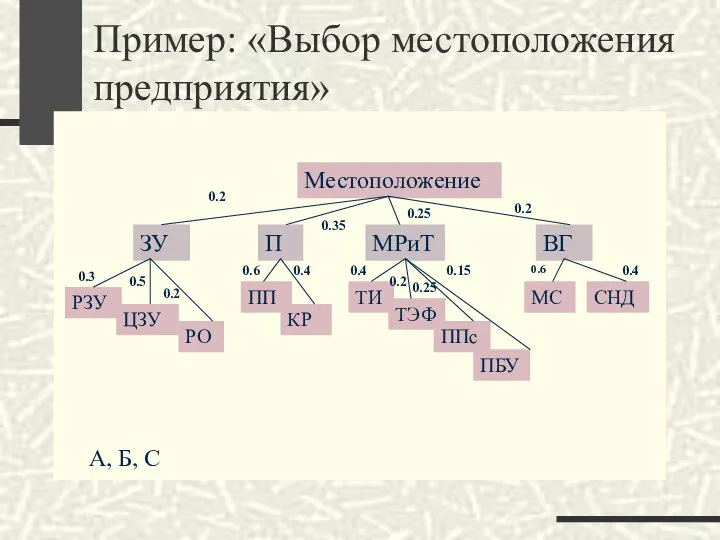
- 51. Пример: «Выбор местоположения предприятия» Местоположение ЗУ Местоположение П МРиТ ВГ РЗУ ЦЗУ РО ПП КР ТИ
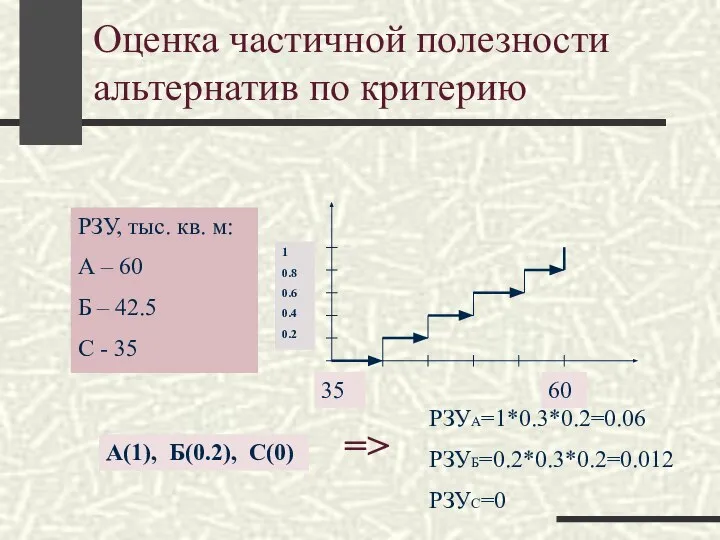
- 52. Оценка частичной полезности альтернатив по критерию РЗУ, тыс. кв. м: А – 60 Б – 42.5
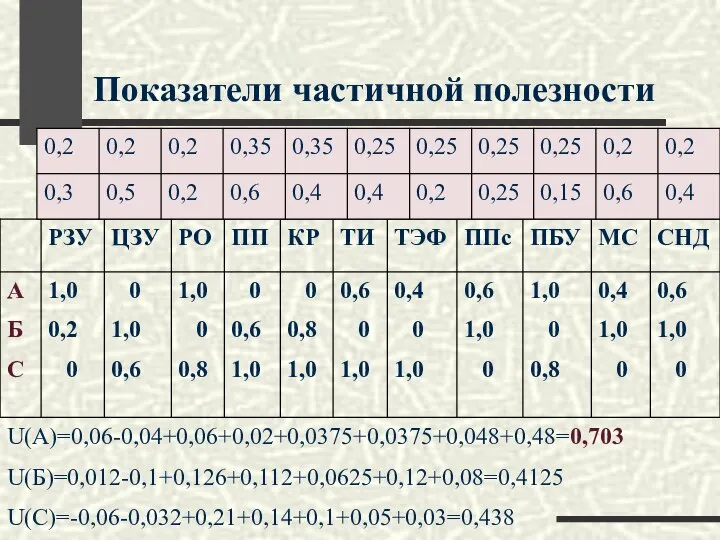
- 53. Показатели частичной полезности U(A)=0,06-0,04+0,06+0,02+0,0375+0,0375+0,048+0,48=0,703 U(Б)=0,012-0,1+0,126+0,112+0,0625+0,12+0,08=0,4125 U(C)=-0,06-0,032+0,21+0,14+0,1+0,05+0,03=0,438
- 54. Применение «+»: Относительно простой способ нахождения решения в МКЗ путем системного структурирования и легкой интерпретации результатов
- 56. Скачать презентацию


































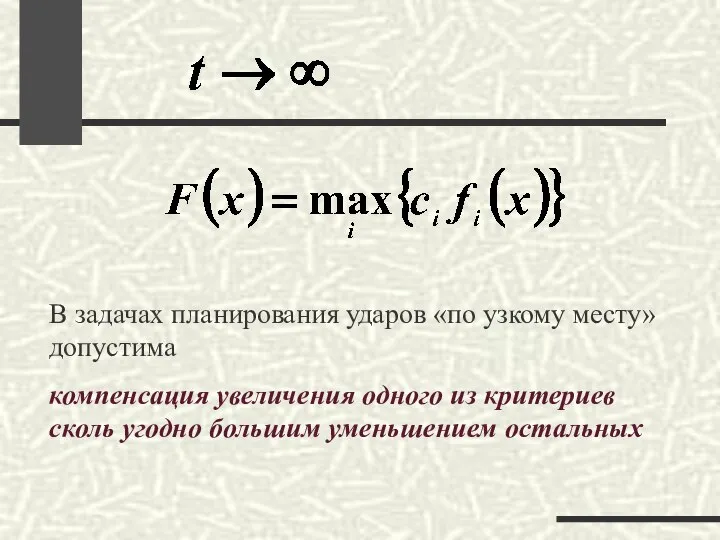




 Powołanie zakonne
Powołanie zakonne CCNA RS 6.0 Bridging. Шаблон
CCNA RS 6.0 Bridging. Шаблон «Букет роз» (материал-пластилин) Урок художественного труда 3 класс
«Букет роз» (материал-пластилин) Урок художественного труда 3 класс Роль СМИ в политической жизни
Роль СМИ в политической жизни Отчет по учебной практике. Радарный уровнемер Saab TankRadar RTG 3920
Отчет по учебной практике. Радарный уровнемер Saab TankRadar RTG 3920 Осушение слабопроницаемых пород
Осушение слабопроницаемых пород Пакет Яровой
Пакет Яровой Сертификация сыра
Сертификация сыра Презентация Понятие законности
Презентация Понятие законности Велогонка Пермь - "Демидково"
Велогонка Пермь - "Демидково" Систематизация и классификация знаний в судебной экспертизе
Систематизация и классификация знаний в судебной экспертизе Приметы и суеверия Германии и России
Приметы и суеверия Германии и России Жизнь и служение Иоанна Кронштадтского
Жизнь и служение Иоанна Кронштадтского Презентацию подготовила учитель МБОУ «Верх-Обская СОШ им. М. С. Евдокимова» Ларионова Е.А.
Презентацию подготовила учитель МБОУ «Верх-Обская СОШ им. М. С. Евдокимова» Ларионова Е.А. Основные виды сырья для производства строительных материалов. Лекция 4
Основные виды сырья для производства строительных материалов. Лекция 4 Презентация "Цены" - скачать презентации по Экономике
Презентация "Цены" - скачать презентации по Экономике Разработка стратегических установок организации. Тема 3
Разработка стратегических установок организации. Тема 3 Глава 21. Консультирование по вопросам всеобщего управления качеством
Глава 21. Консультирование по вопросам всеобщего управления качеством Програми з графічним інтерфейсом. Робота з проектами у середовищі Lazarus
Програми з графічним інтерфейсом. Робота з проектами у середовищі Lazarus наложение ареста на почтово-телеграфные отправления, их осмотр и выемка
наложение ареста на почтово-телеграфные отправления, их осмотр и выемка Функции политики
Функции политики Страхування життя
Страхування життя Программирование в EV3. Проезды и повороты
Программирование в EV3. Проезды и повороты Brand: Do It Yourself
Brand: Do It Yourself  По большому счету, БРЕНДИНГ решает все! HR-бренд или бренд работодателя это: Образ, имидж вашей компании как хорошего места работы в
По большому счету, БРЕНДИНГ решает все! HR-бренд или бренд работодателя это: Образ, имидж вашей компании как хорошего места работы в  «Скажи мне - и я забуду, Покажи мне - и я запомню, Дай сделать - и я пойму».
«Скажи мне - и я забуду, Покажи мне - и я запомню, Дай сделать - и я пойму». Химия элементов D-ЭЛЕМЕНТы 7-8
Химия элементов D-ЭЛЕМЕНТы 7-8  Методы исследований
Методы исследований