Содержание
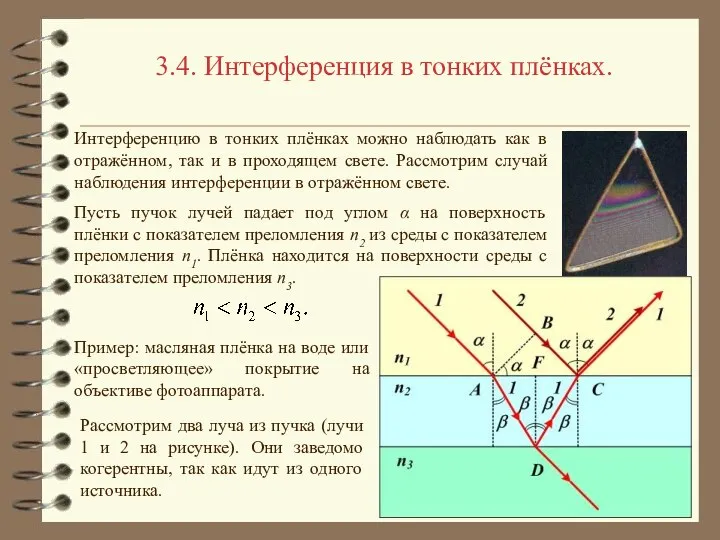
- 2. 3.4. Интерференция в тонких плёнках. Интерференцию в тонких плёнках можно наблюдать как в отражённом, так и
- 3. 3.4. Интерференция в тонких плёнках. Луч 1 проходит в плёнку, отражается от её нижней границы и
- 4. 3.4. Интерференция в тонких плёнках. λ/2 добавлена потому, в точке D происходит отражение от оптически более
- 5. 3.4. Интерференция в тонких плёнках.
- 6. 3.4. Интерференция в тонких плёнках.
- 7. 3.4. Интерференция в тонких плёнках.
- 8. 3.4. Интерференция в тонких плёнках.
- 9. 3.4. Интерференция в тонких плёнках. Вспомним условия минимума и максимума при интерференции В случае интерференции лучей,
- 10. 3.4. Интерференция в тонких плёнках. Величина показателя преломления третьей среды в явном виде в формулы не
- 11. 3.4. Интерференция в тонких плёнках. Максимум: Минимум: Максимум:
- 12. 3.4. Интерференция в тонких плёнках. Минимум: Итак, для случая например, для случая, когда плёнка находится в
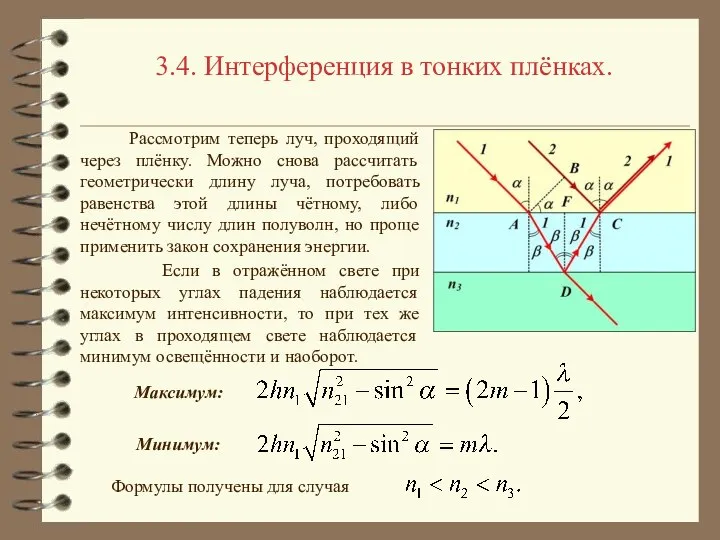
- 13. 3.4. Интерференция в тонких плёнках. Рассмотрим теперь луч, проходящий через плёнку. Можно снова рассчитать геометрически длину
- 14. 3.4. Интерференция в тонких плёнках. Для случая проходящих волн, когда плёнка находится в воздухе, Минимум: Максимум:
- 15. 3.5. Кольца Ньютона.
- 16. 3.5. Кольца Ньютона. Если на стеклянную пластину положить линзу, то наблюдая в отражённом свете, можно увидеть
- 17. 3.5. Кольца Ньютона. Рассмотрим ход лучей при наблюдении в отражённом свете. Луч 1 преломляется на поверхности
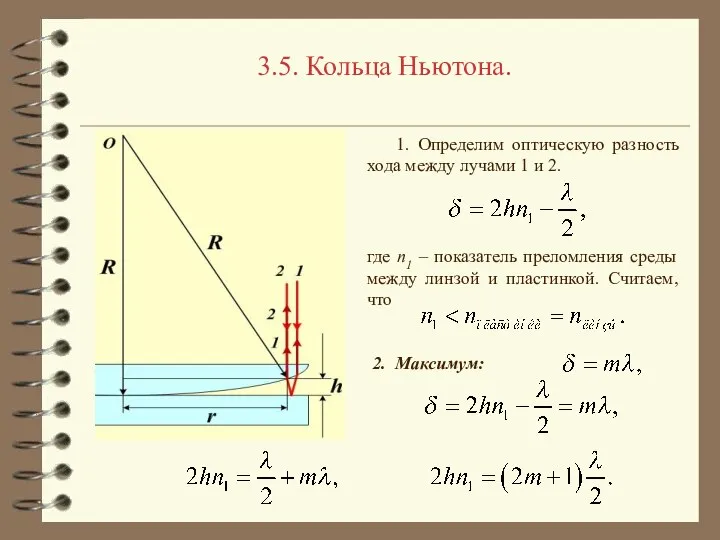
- 18. 3.5. Кольца Ньютона. 1. Определим оптическую разность хода между лучами 1 и 2. где n1 –
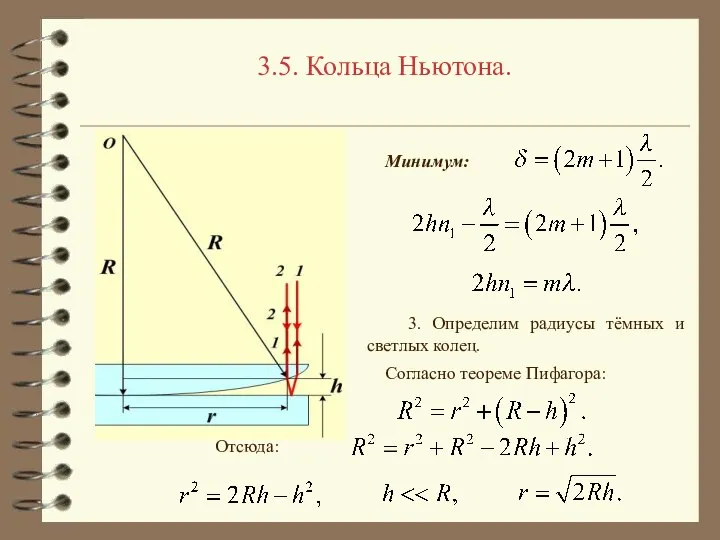
- 19. 3.5. Кольца Ньютона. Минимум: 3. Определим радиусы тёмных и светлых колец. Согласно теореме Пифагора: Отсюда:
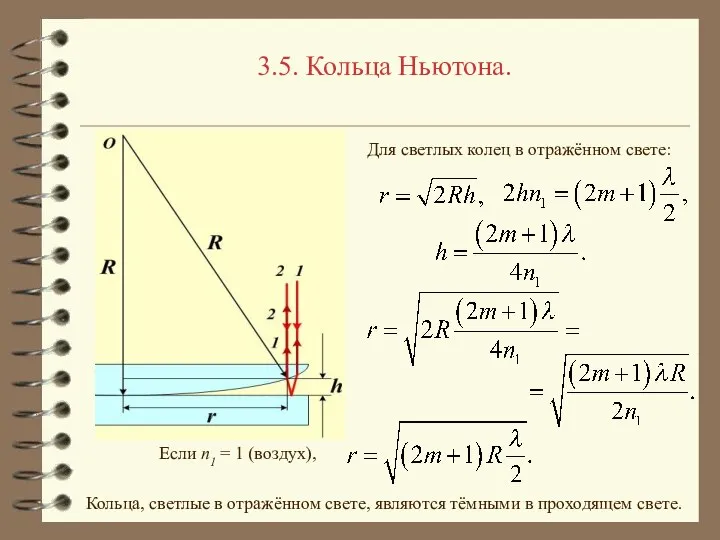
- 20. 3.5. Кольца Ньютона. Для тёмных колец в отражённом свете: Если n1 = 1 (воздух), Кольца, тёмные
- 21. 3.5. Кольца Ньютона. Для светлых колец в отражённом свете: Если n1 = 1 (воздух), Кольца, светлые
- 22. 3.6. Интерферометры.
- 23. 3.6. Интерферометры. Оптические интерферометры – приборы для измерения длин волн спектральных линий и их структуры. Их
- 24. 3.6. Интерферометры. Оптическая схема интерферометра Майкельсона
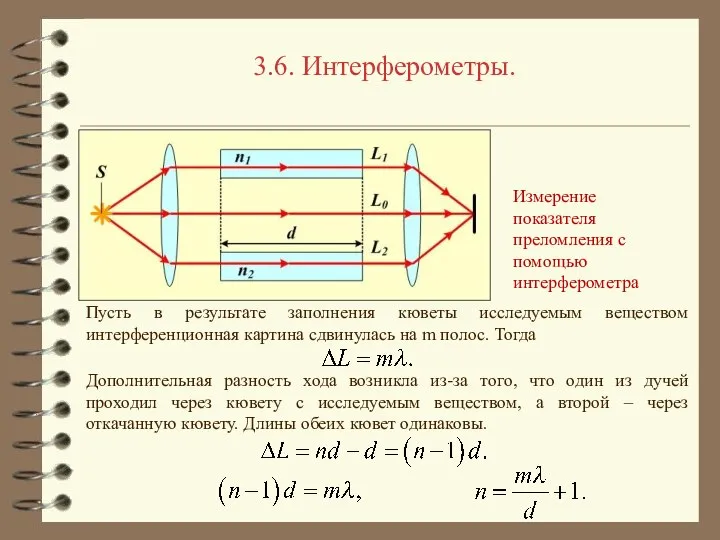
- 25. 3.6. Интерферометры. Измерение показателя преломления с помощью интерферометра Пусть в результате заполнения кюветы исследуемым веществом интерференционная
- 26. 3.7. Примеры решения задач.
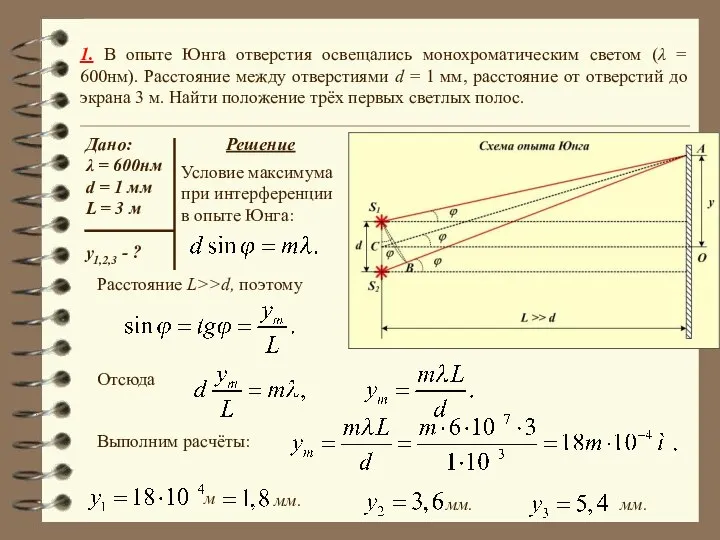
- 27. 1. В опыте Юнга отверстия освещались монохроматическим светом (λ = 600нм). Расстояние между отверстиями d =
- 28. 2. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света d = 0,5 мм,
- 29. 2. В опыте с зеркалами Френеля расстояние между мнимыми изображениями источника света d = 0,5 мм,
- 30. 3. В опыте Юнга на пути одного интерферирующего луча помещается стеклянная пластинка перпендикулярно к лучу. Вследствие
- 31. 4. На мыльную плёнку падает белый свет под углом i = 45° к поверхности плёнки. При
- 32. 4. На мыльную плёнку падает белый свет под углом i = 45° к поверхности плёнки. При
- 33. 4. На мыльную плёнку падает белый свет под углом i = 45° к поверхности плёнки. При
- 34. 15. На поверхность стеклянного объектива (nc = 1,5) нанесена тонкая плёнка, показатель преломления которой n =
- 35. 15. На поверхность стеклянного объектива (nc = 1,5) нанесена тонкая плёнка, показатель преломления которой n =
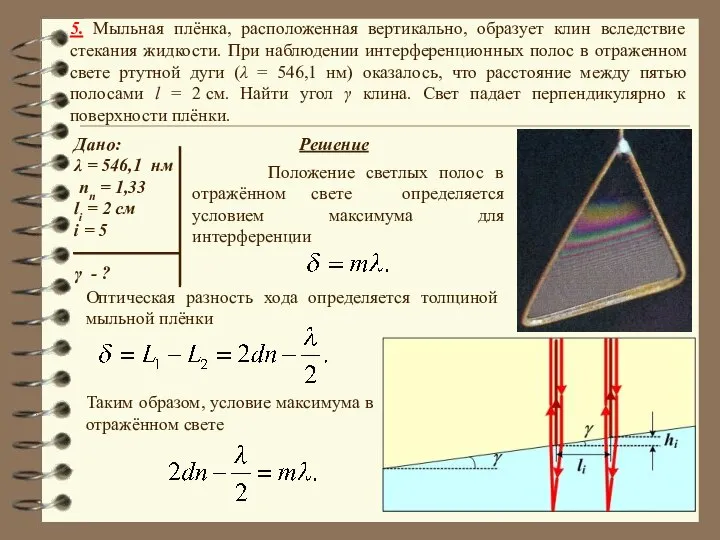
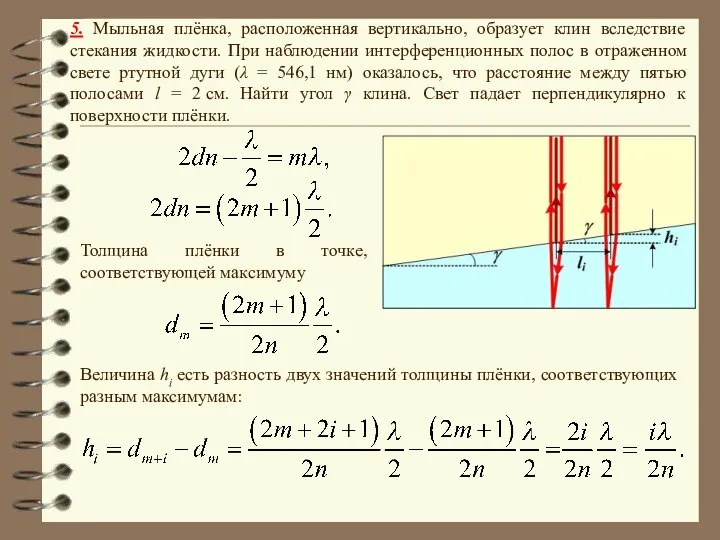
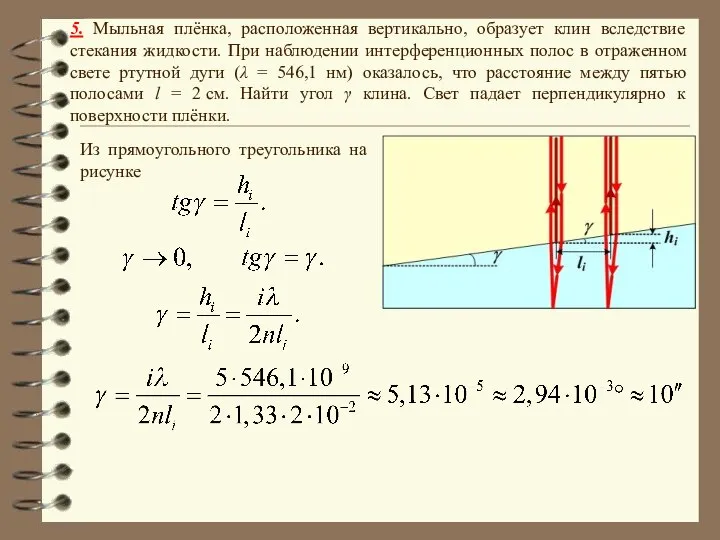
- 36. 5. Мыльная плёнка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном
- 37. 5. Мыльная плёнка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном
- 38. 5. Мыльная плёнка, расположенная вертикально, образует клин вследствие стекания жидкости. При наблюдении интерференционных полос в отраженном
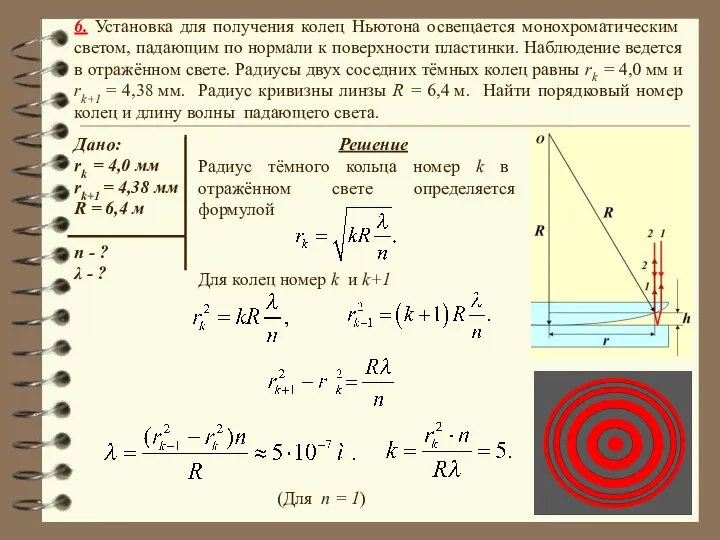
- 39. 6. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение
- 40. 10. Установка для наблюдения колец Ньютона освещена светом с длиной волны λ = 589 нм, падающим
- 41. 11. Установка для наблюдения колец Ньютона освещена монохроматическим светом с длиной волны λ = 500 нм,
- 43. Скачать презентацию





























 Мастер – класс по пластичной замше. Фоамиран
Мастер – класс по пластичной замше. Фоамиран Ordnungszahlen
Ordnungszahlen Русская культура XIX века (ЕГЭ)
Русская культура XIX века (ЕГЭ) На что способен наш мозг Ученица 2 «а» класса Егорова Вероника
На что способен наш мозг Ученица 2 «а» класса Егорова Вероника Bukin Avenue. Бизнес-проект
Bukin Avenue. Бизнес-проект Виктор Федорович Янукович - президент Украины с 25 февраля 2010 года по 22 февраля 2014 года
Виктор Федорович Янукович - президент Украины с 25 февраля 2010 года по 22 февраля 2014 года Турбонаддув. Турбированный бензиновый двигатель
Турбонаддув. Турбированный бензиновый двигатель ВКР: Гражданско – правовое регулирование отношений строительного подряда
ВКР: Гражданско – правовое регулирование отношений строительного подряда Пересечение многогранников проецирующей плоскостью
Пересечение многогранников проецирующей плоскостью Прецептрон
Прецептрон Etika_biznesa
Etika_biznesa Пропорционирование в храмовом зодчестве Северного Кавказа
Пропорционирование в храмовом зодчестве Северного Кавказа Образовательный курс «МАРКЕТИНГОВЫЕ СЕРВИСЫ» Киев, Украина, 2014 год
Образовательный курс «МАРКЕТИНГОВЫЕ СЕРВИСЫ» Киев, Украина, 2014 год  Чит илләрдәге татарлар
Чит илләрдәге татарлар Теоретические языки запросов в реляционных БД
Теоретические языки запросов в реляционных БД Средства стимулирования сбыта: Виды и особенности Выполнил
Средства стимулирования сбыта: Виды и особенности Выполнил Диоды с переменной емкостью
Диоды с переменной емкостью . Биосоциальная природа человека
. Биосоциальная природа человека Singapore International Arbitration Centre
Singapore International Arbitration Centre Презентация Основные положения концепции социально-ориентированного управления внутренними стейкхолдерами
Презентация Основные положения концепции социально-ориентированного управления внутренними стейкхолдерами Финансовое обеспечение деятельности образовательных учреждений
Финансовое обеспечение деятельности образовательных учреждений  Презентация "Учет кассовых операций" - скачать презентации по Экономике
Презентация "Учет кассовых операций" - скачать презентации по Экономике Основы С#. Наследование классов. Абстрактные методы и полиморфизм. (Лекция 8.1)
Основы С#. Наследование классов. Абстрактные методы и полиморфизм. (Лекция 8.1) Современные энергосберегающие технологии. Пассивные дома
Современные энергосберегающие технологии. Пассивные дома Правовое регулирование международного договора купли продажи
Правовое регулирование международного договора купли продажи  Система стандартов по информации, библиотечному и издательскому делу. Организационно-распорядительная документация
Система стандартов по информации, библиотечному и издательскому делу. Организационно-распорядительная документация Е1 біріншілік цифрлық ағынынның циклының құрылуы
Е1 біріншілік цифрлық ағынынның циклының құрылуы Скульптура
Скульптура