Содержание
- 2. Берман Г.Н. Сборник задач по курсу математического анализа: учеб пособие. СПб.: Лань, 2007. – 448 с.
- 3. §1. Исследование функций при помощи производных. Возрастание и убывание функции §2. Максимум и минимум функции. Наибольшее
- 4. §1. Исследование функций при помощи производных. Возрастание и убывание функции
- 5. §1. … Возрастание и убывание функции (продолжение)
- 6. Т е о р е м а 2 (достаточные условия, ⇐). Если функция y = f(x)
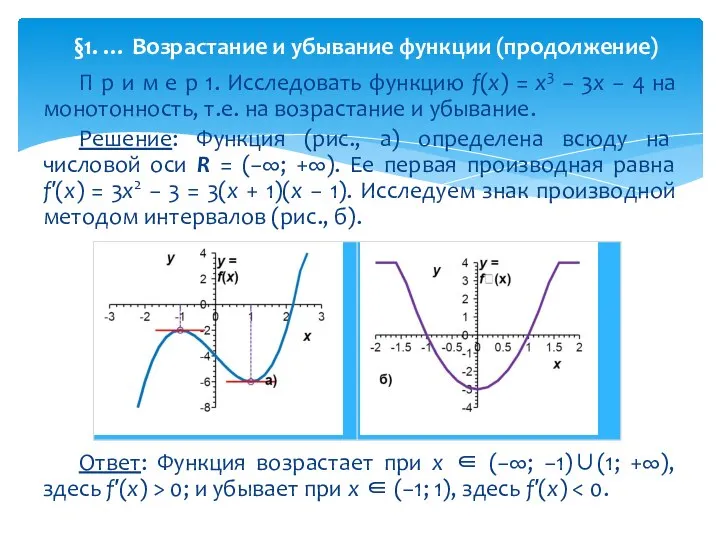
- 7. П р и м е р 1. Исследовать функцию f(x) = x3 − 3x − 4
- 8. Df: Точка x0 называется точкой (локального) максимума функции y = f(x) (см. рис. из примера 1),
- 9. §2. Максимум и минимум функции … (продолжение)
- 10. З а м е ч а н и я: 1. Геометрически равенство f′(x0) = 0 означает,
- 11. Т е о р е м а 4 (достаточное условие экстремума). Если непрерывная функция y =
- 12. Отсюда следует, что значение f(x = x0) в точке x0 является наибольшим на интервале (x0 −
- 13. §2. Максимум и минимум функции … (продолжение) x 0 8 f′(x) max + min + −
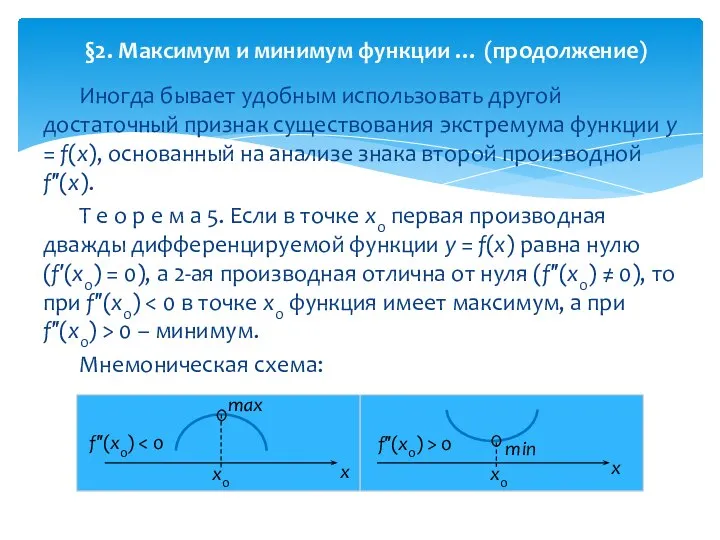
- 14. Иногда бывает удобным использовать другой достаточный признак существования экстремума функции y = f(x), основанный на анализе
- 15. §2. Максимум и минимум функции … (продолжение)
- 16. Пусть функция y = f(x) непрерывна на отрезке [a; b]. Как известно (теорема Вейерштрасса), такая функция
- 17. Правила исследования функции y = f(x), заданной на отрезке [a; b] на наибольшее и наименьшее значения:
- 18. П р и м е р 3. Найти наибольшее и наименьшее значения функции f(x) = 3x4
- 19. §2. … Наибольшее и наименьшее значения функции на отрезке (продолжение) x y 2R
- 20. §2. … Наибольшее и наименьшее значения функции на отрезке (продолжение)
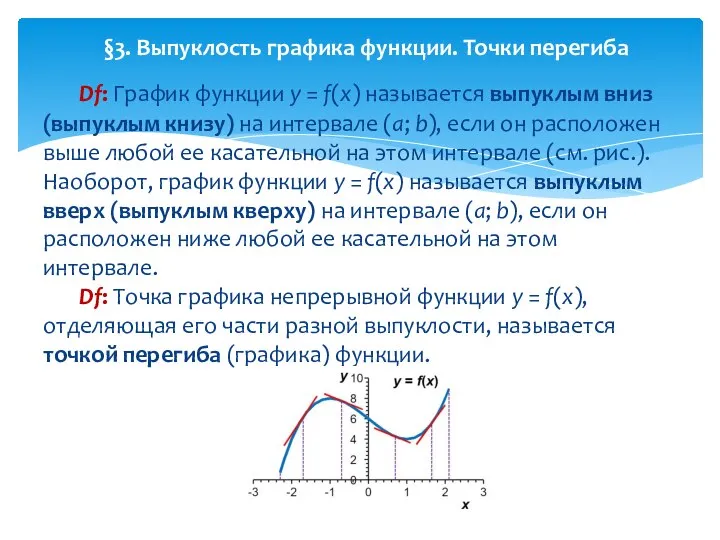
- 21. Df: График функции y = f(x) называется выпуклым вниз (выпуклым книзу) на интервале (a; b), если
- 22. Интервалы выпуклости вниз и вверх находят с помощью следующей теоремы. Т е о р е м
- 23. Для нахождения точек перегиба графика функции используется следующая теорема. Т е о р е м а
- 24. П р и м е р 7. Исследовать на выпуклость и точки перегиба график функции y
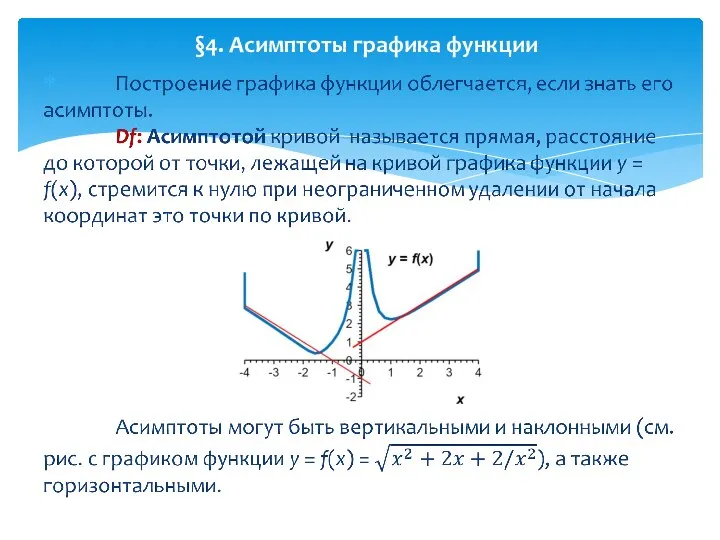
- 25. §4. Асимптоты графика функции
- 26. §4. Асимптоты графика функции (продолжение)
- 27. Df: Если уравнение асимптоты имеет вид y = kx + b, где k – конечное число,
- 28. §4. Асимптоты графика функции (продолжение)
- 29. §4. Асимптоты графика функции (продолжение)
- 30. §4. Асимптоты графика функции (продолжение)
- 31. Исследование функции y = f(x) целесообразно вести в определенной последовательности (см. далее). З а м е
- 32. Правила (схема) исследования функции y = f(x) и построения ее графика: 1) Найти область определения функции.
- 33. §5. Общая схема исследования функции … (продолжение)
- 34. §5. Общая схема исследования функции … (продолжение)
- 35. §5. Общая схема исследования функции … (продолжение)
- 36. §5. Общая схема исследования функции … (продолжение)
- 38. Скачать презентацию












![Пусть функция y = f(x) непрерывна на отрезке [a; b]. Как](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1305112/slide-15.jpg)
![Правила исследования функции y = f(x), заданной на отрезке [a; b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1305112/slide-16.jpg)

















 Мастер-Кулибин из деревни Бурундуки Герасимов Артур Николаевич
Мастер-Кулибин из деревни Бурундуки Герасимов Артур Николаевич Пришла Коляда
Пришла Коляда Субъекты международного таможенного сотрудничества
Субъекты международного таможенного сотрудничества . ОГЭ_обществознание_политология
. ОГЭ_обществознание_политология . Великие державы
. Великие державы Проецирование плоскости
Проецирование плоскости Система охолодження двигунів автомобіля
Система охолодження двигунів автомобіля Система работы ОУ по проблемам преемственности
Система работы ОУ по проблемам преемственности Российская империя в 20 веке
Российская империя в 20 веке «В мастерской античного скульптора» Работу выполнили Тетеркина Кристина, Захваткина Александра, гр 1301
«В мастерской античного скульптора» Работу выполнили Тетеркина Кристина, Захваткина Александра, гр 1301  Особливості вигодовування недоношених новонароджених. Поняття про “вільне” вигодовування, його форми і показання до призначення.
Особливості вигодовування недоношених новонароджених. Поняття про “вільне” вигодовування, його форми і показання до призначення.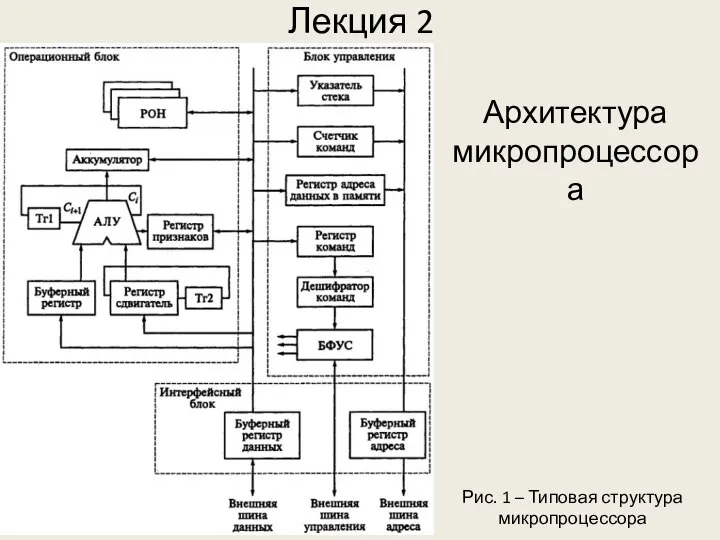 Архитектура микропроцессора
Архитектура микропроцессора Баскетбол комплекс упражнений для разминки «ведение мяча»
Баскетбол комплекс упражнений для разминки «ведение мяча» Serfer
Serfer  Производные типы данных. (Лекция 3)
Производные типы данных. (Лекция 3) Презентация на тему "Спортивные инициативы" - скачать презентации по Педагогике
Презентация на тему "Спортивные инициативы" - скачать презентации по Педагогике Художественная культура в первой половине XIX века
Художественная культура в первой половине XIX века Презентация на тему: понятие, структура и основные полномочия научного центра правовой информации при Министерстве юстиции РФ
Презентация на тему: понятие, структура и основные полномочия научного центра правовой информации при Министерстве юстиции РФ «Разработка, экспертиза и апробация инструментария и процедур оценки качества на ступени основного общего образования (5-8 кл
«Разработка, экспертиза и апробация инструментария и процедур оценки качества на ступени основного общего образования (5-8 кл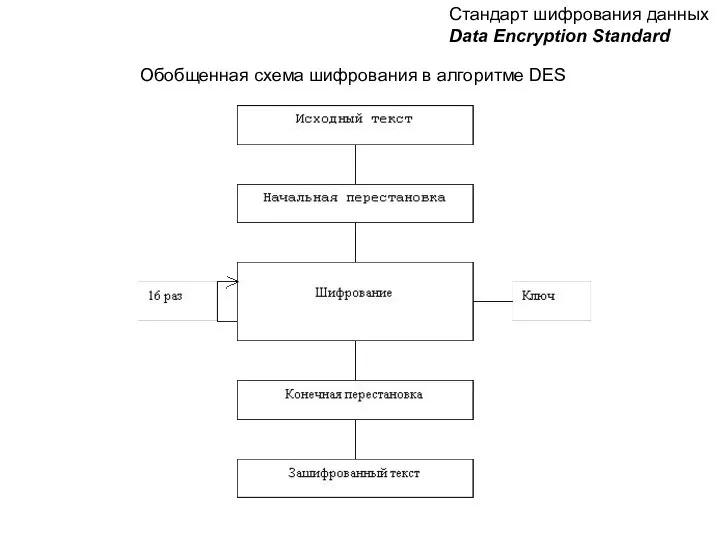 DES
DES  Шарпан – головной убор замужней женщины. Вышивка
Шарпан – головной убор замужней женщины. Вышивка Пожежні автомобілі аеродромної служби
Пожежні автомобілі аеродромної служби Неоднородные системы и способы их разделения. Отстаивание
Неоднородные системы и способы их разделения. Отстаивание Презентація учнівського колективу 5-А класу нова
Презентація учнівського колективу 5-А класу нова V.A.C. ТЕРАПИЯ В ЛЕЧЕНИИ РАН
V.A.C. ТЕРАПИЯ В ЛЕЧЕНИИ РАН Управление световым оформлением зданий
Управление световым оформлением зданий Строковый тип данных String
Строковый тип данных String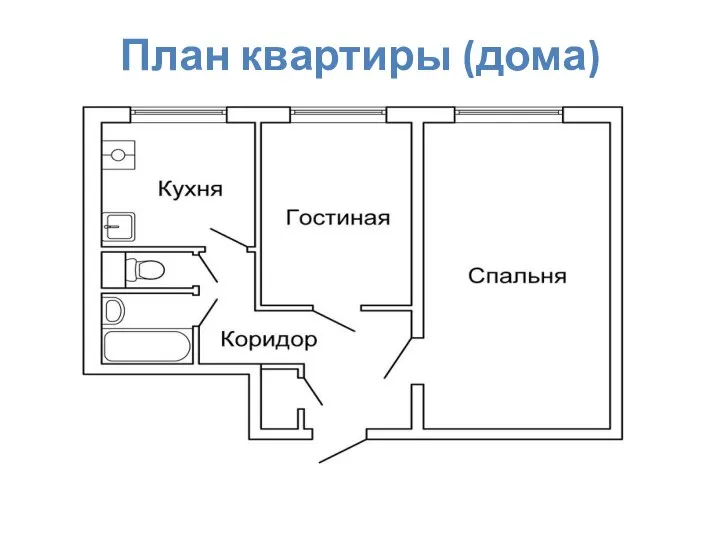 План квартиры (дома)
План квартиры (дома)