Кинематика

Раздел 1. Классическая и релятивистская механика

Темы лекций
Кинематика поступательного и вращательного движений.
Динамика

Основная литература: учебники
1. Савельев И.В. Курс общей физики: Т.1. Механика.

Дополнительная литература по теоретической части

1. Калистратова Л.Ф., Гладенко А.А., Ярош

Литература для практических и домашних заданий

1. Бердинская Н.В., Нижникова О.В., Ясько

3. Калистратова Л.Ф., Волкова В.К., Лях О.В., Павловская О.Ю. Физика

Литература для подготовки к тестовой сдаче коллоквиума

1. Калистратова Л.Ф., Калистратова Н.П.,

3. Павловская О.Ю., Туровец А.Г., Ясько С.С., Калистратова Н.П. Законы сохранения.

Тема 1. Кинематика поступательного и вращательного движений

План лекции
1.1. Введение.
1.2. Кинематика

1.1. ВВЕДЕНИЕ

Механическое движение – это процесс изменения расположения тел или их

Классическая механика

Классическую механику создал И. Ньютон.
Он постулировал, что время и

Классические свойства пространства

Абсолютное пространство
- трехмерно (имеет три измерения),
- непрерывно (его

Классические свойства времени

Абсолютное время
- одномерно (имеет одно измерение),
- непрерывно

Релятивистская и квантовая механики

В начале ХХ века классическая механика подверглась кардинальному

Теория относительности

Теория относительности установила:
1) пространство и время не являются самостоятельными объектами;

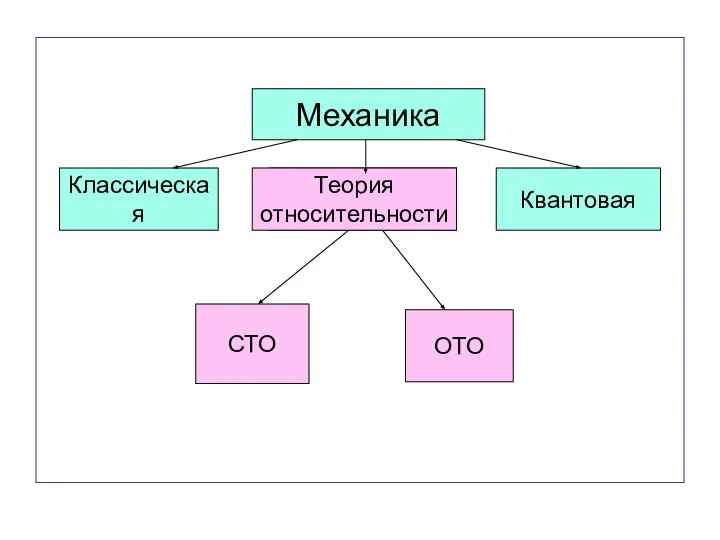
Механика

Классическая

Квантовая

Теория
относительности

СТО

ОТО

Объекты механики
Макроскопические тела, движущиеся с малыми скоростями, изучает классическая механика.
Макроскопические тела

Микроскопические тела (микрочастицы), движущиеся с большими, но нерелятивистскими скоростями, изучает квантовая

Разделы механики

Механика состоит из трех разделов – кинематики, динамики и статики.
Кинематика

Основные понятия механики

Движение – изменение положения тел друг относительно друга.
Тело отсчёта

1.2. Кинематика поступательного движения материальной точки

Описать движение материальной точки – значит

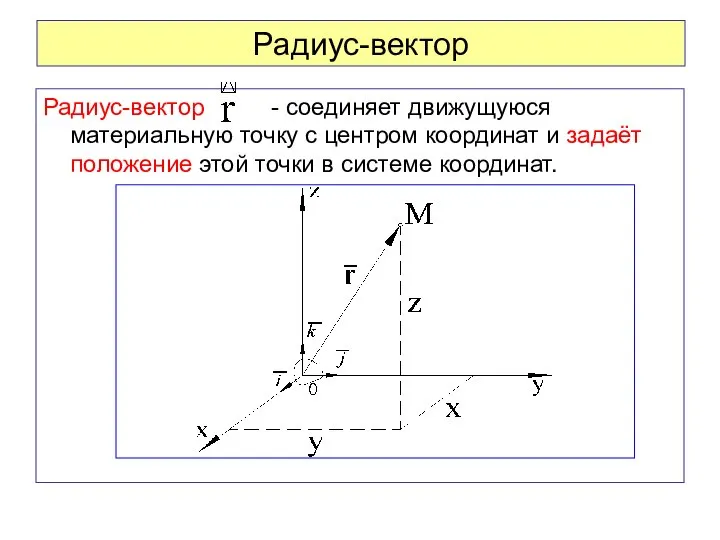
Радиус-вектор

Радиус-вектор - соединяет движущуюся материальную точку с центром координат и задаёт

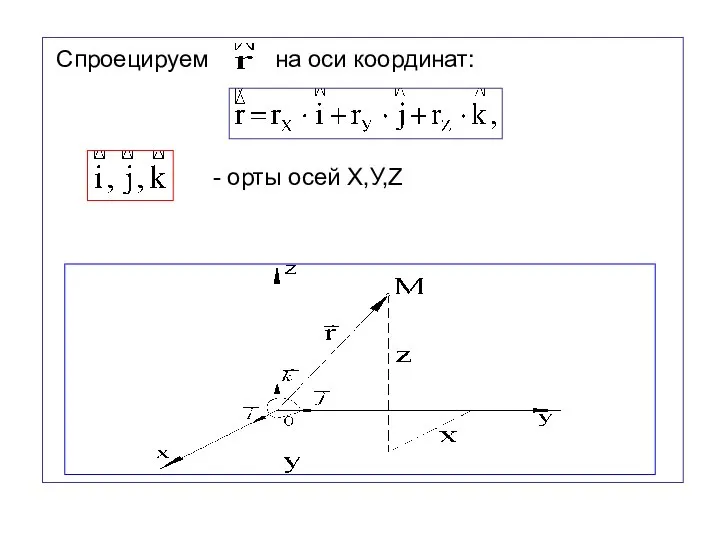
Спроецируем на оси координат:
- орты осей Х,У,Z

Закон движения

В процессе движения материальной точки её радиус-вектор изменяется по величине

Кинематические уравнения движения

Закон движения, записанный в скалярной форме, представляет систему уравнений

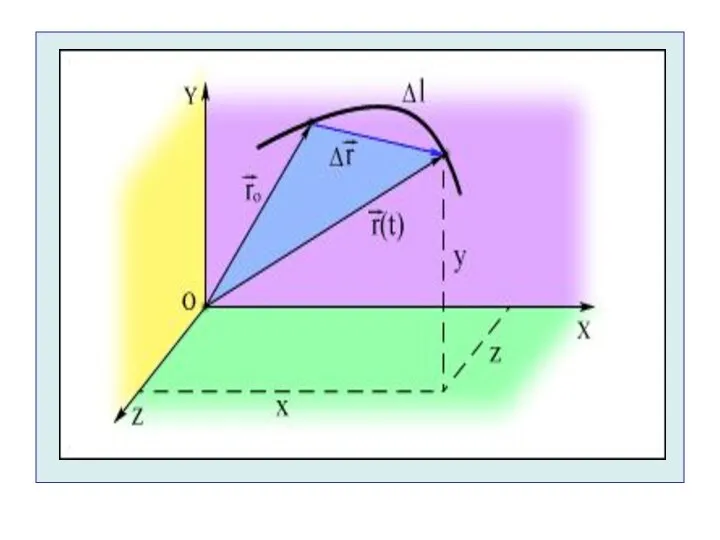
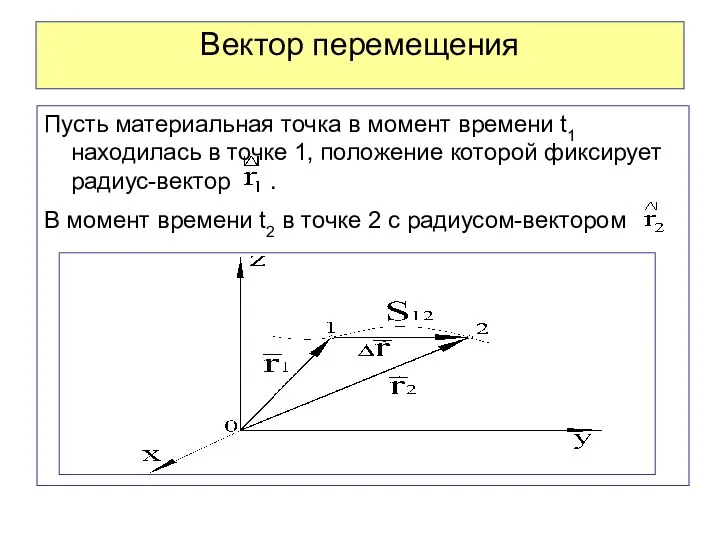
Вектор перемещения

Пусть материальная точка в момент времени t1 находилась в точке

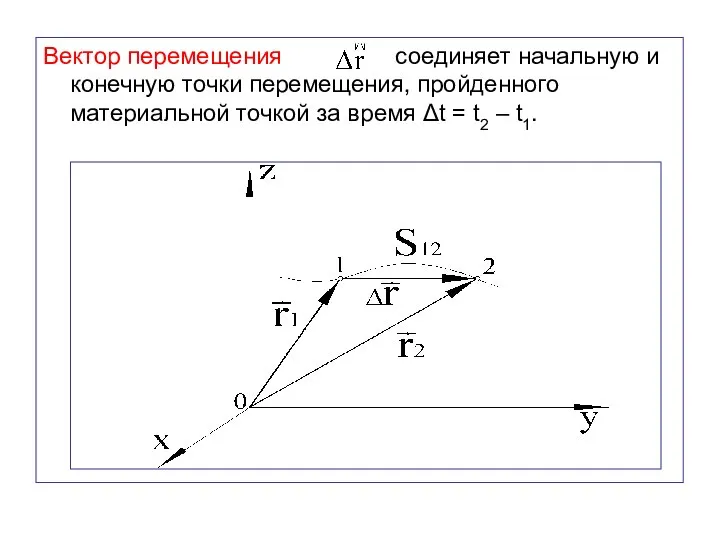
Вектор перемещения соединяет начальную и конечную точки перемещения, пройденного материальной точкой

Путь и перемещение

- приращение радиуса – вектора.
Перемещением называется модуль вектора

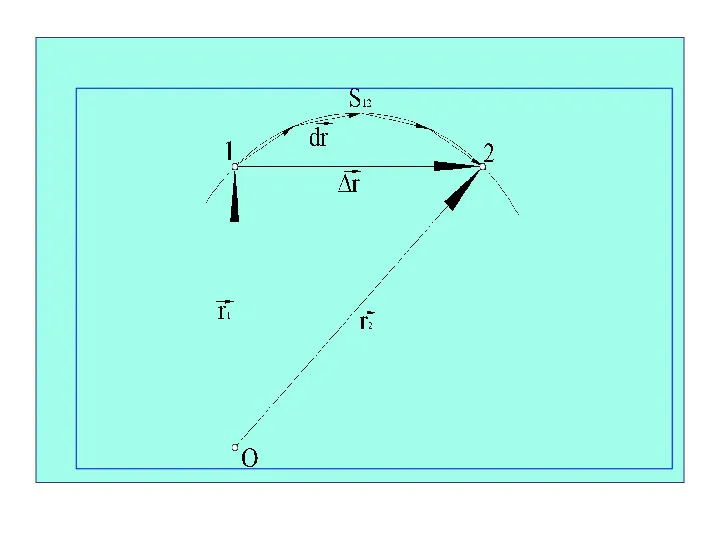
Элементарные путь и перемещение

Элементарное перемещение за бесконечно малый промежуток времени dt

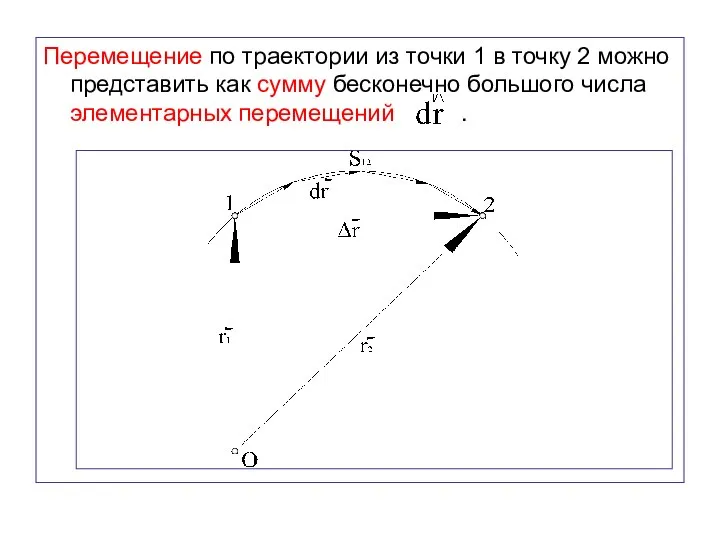
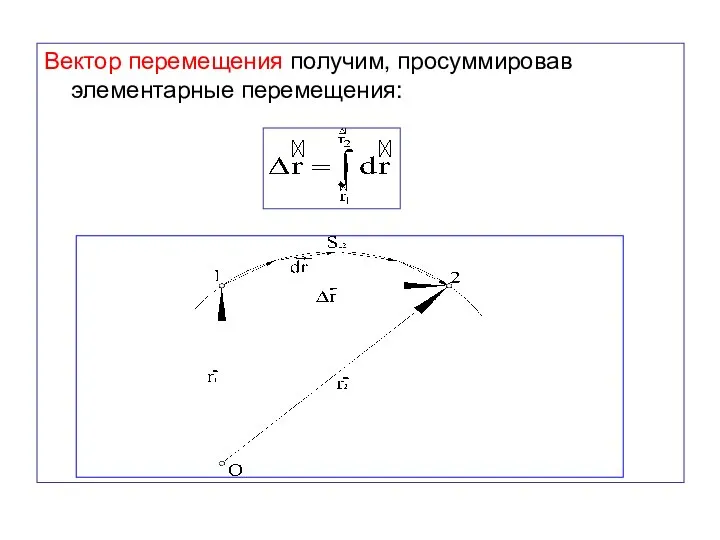
Перемещение по траектории из точки 1 в точку 2 можно представить

Вектор перемещения получим, просуммировав элементарные перемещения:

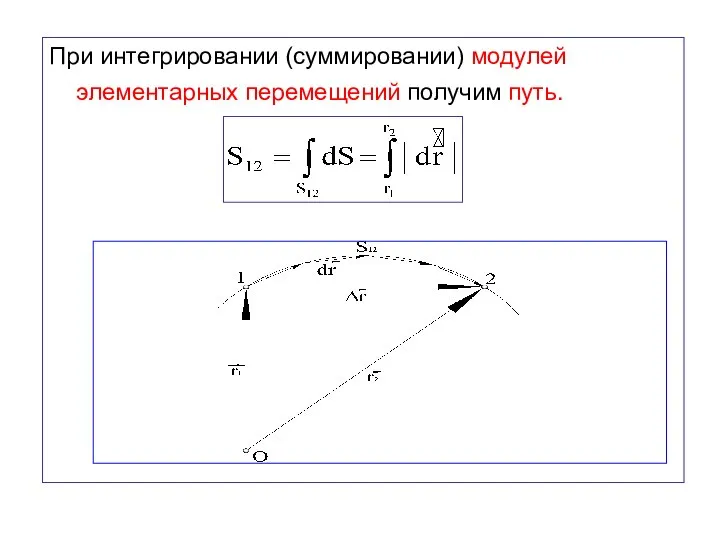
При интегрировании (суммировании) модулей элементарных перемещений получим путь.

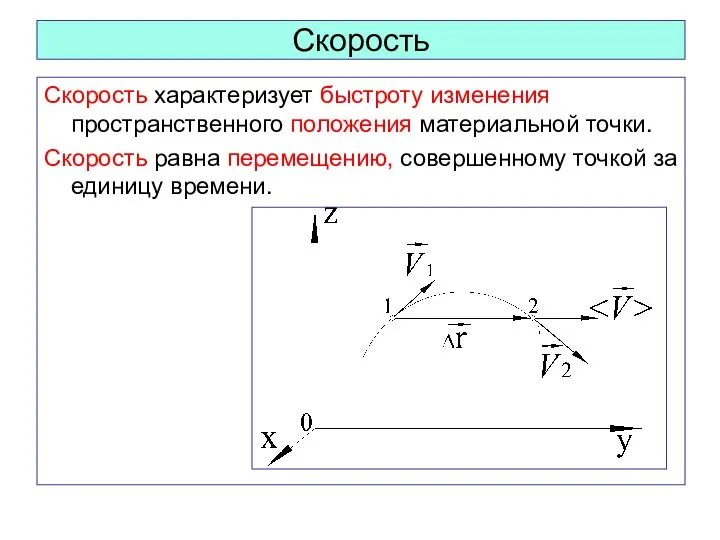
Скорость

Скорость характеризует быстроту изменения пространственного положения материальной точки.
Скорость равна перемещению, совершенному

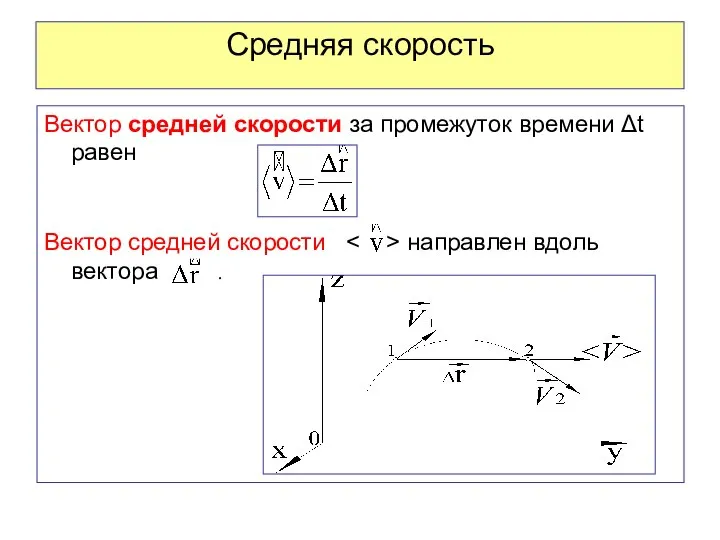
Средняя скорость

Вектор средней скорости за промежуток времени Δt равен
Вектор средней скорости

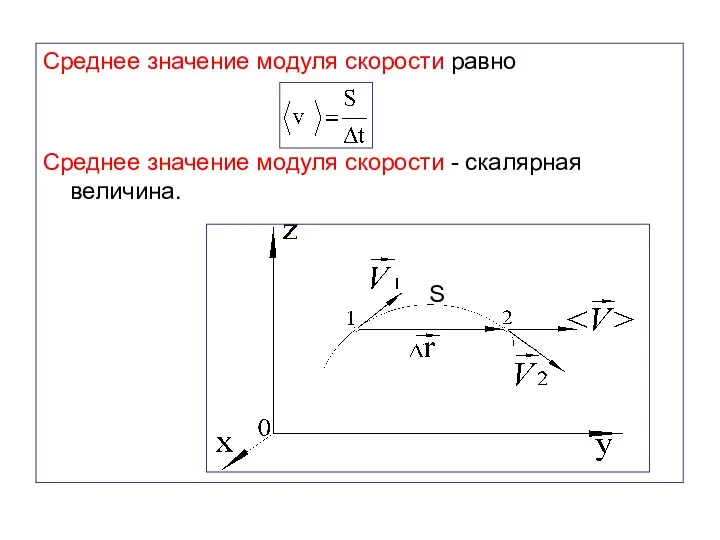
Среднее значение модуля скорости равно
Среднее значение модуля скорости - скалярная величина.

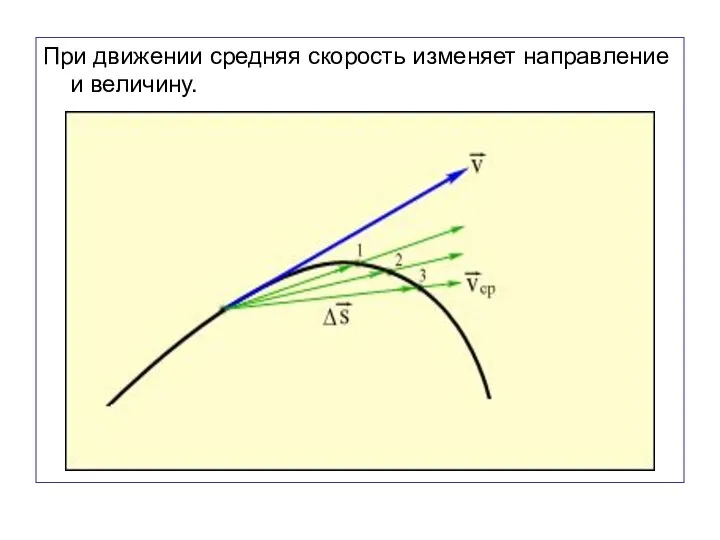
При движении средняя скорость изменяет направление и величину.

Мгновенная скорость

Мгновенная скорость равна пределу вектора средней скорости при неограниченном убывании

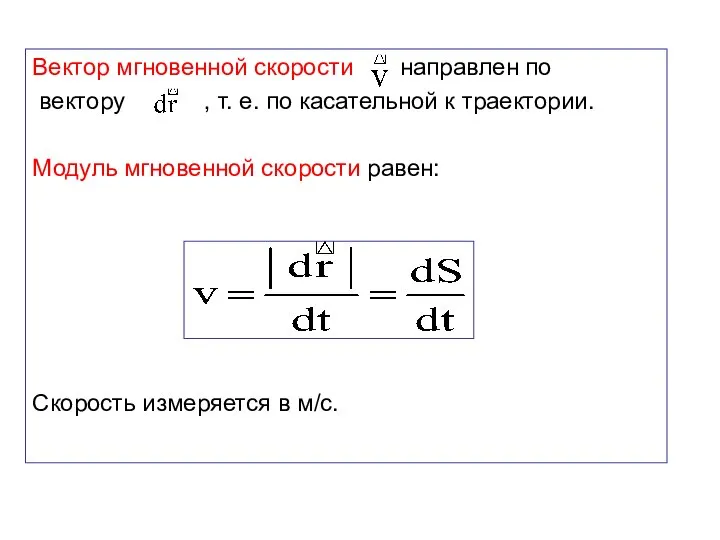
Вектор мгновенной скорости направлен по
вектору , т. е. по касательной

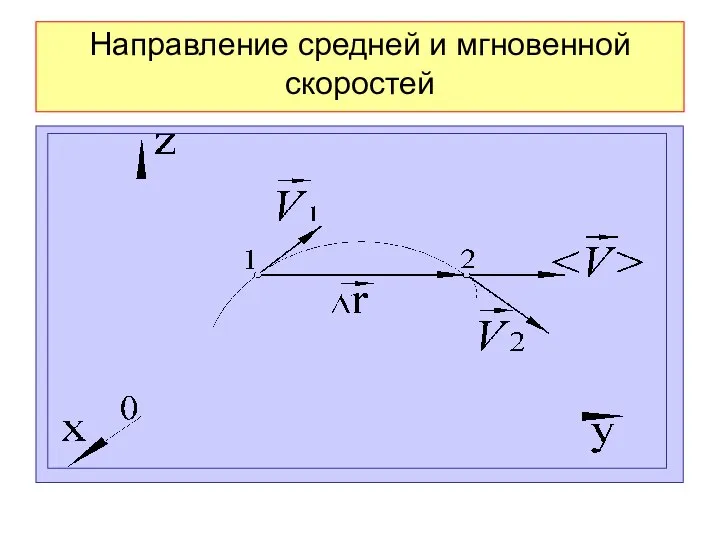
Направление средней и мгновенной скоростей

Проекции скорости на оси координат

Проекции скорости на координатные оси равны первым

Ускорение

В процессе движения материальной точки модуль и направление её скорости в

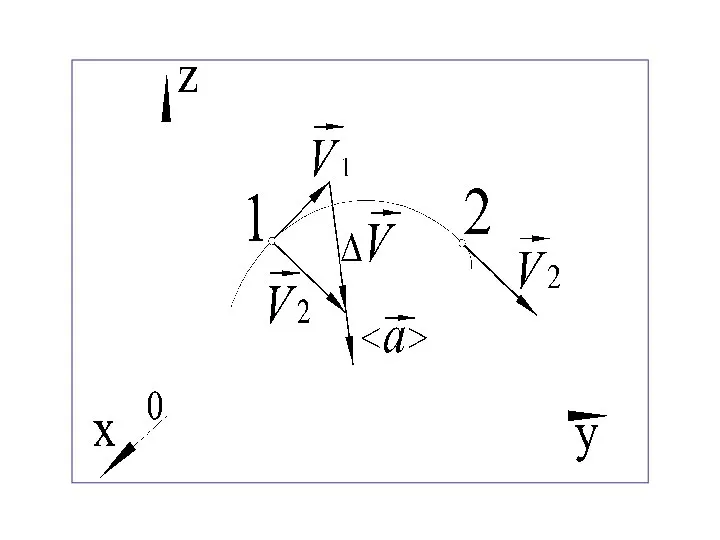
Среднее ускорение

Среднее ускорение за промежуток времени Δt равно
,
где
– приращение скорости

Мгновенное ускорение

Мгновенное ускорение равно пределу, к которому стремится среднее ускорение при

Направление вектора мгновенного ускорения совпадает с направлением вектора , который направлен

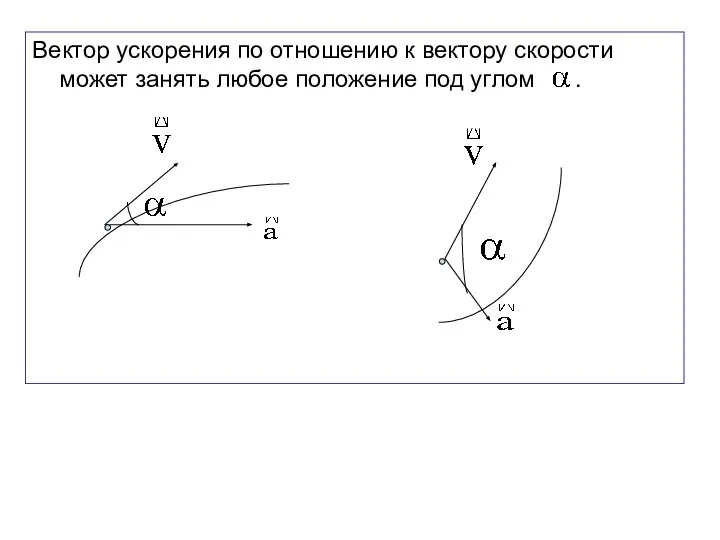
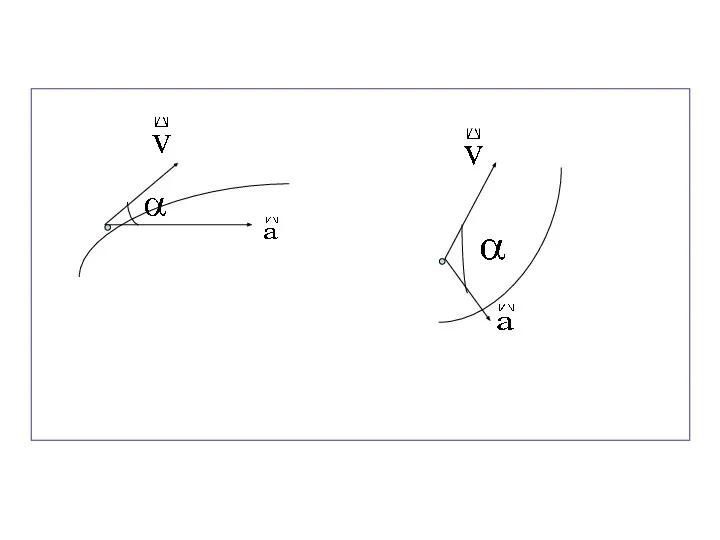
Вектор ускорения по отношению к вектору скорости может занять любое положение

Если угол - острый, то движение материальной точки будет являться ускоренным.

Проекции ускорения

Проекции вектора ускорения на координатные оси:
Вектор мгновенного ускорения и его

Обратная задача кинематики

В рамках кинематики решаются две основные задачи: прямая и

При решении обратной задачи по известной зависимости ускорения от времени ,

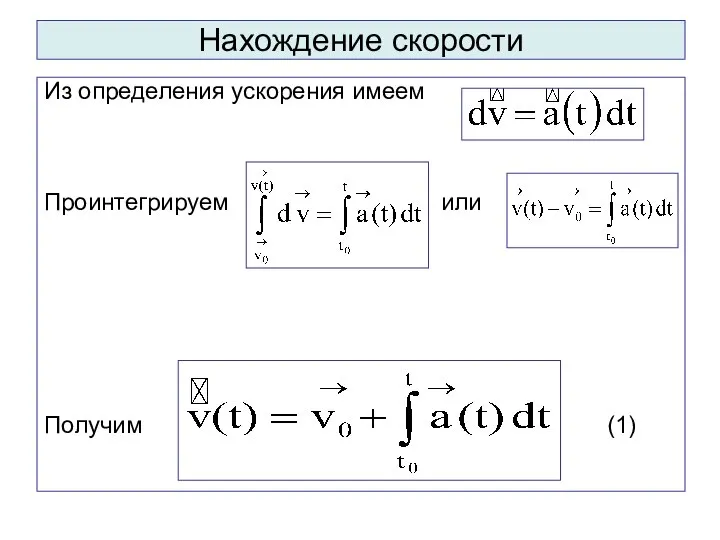
Нахождение скорости

Из определения ускорения имеем
Проинтегрируем или
Получим (1)

Нахождение положения точки

Из определения скорости следует, что элементарное перемещение равно
Подставим сюда

Равномерное движение

Рассмотрим частные случаи.
Равномерное прямолинейное движение
(ускорение = 0 и t0

Равноускоренное движение

2. Равнопеременное прямолинейное движение (ускорение = const и t0 =

1.3. Тангенциальное и нормальное ускорения

Пусть материальная точка движется по криволинейной траектории,

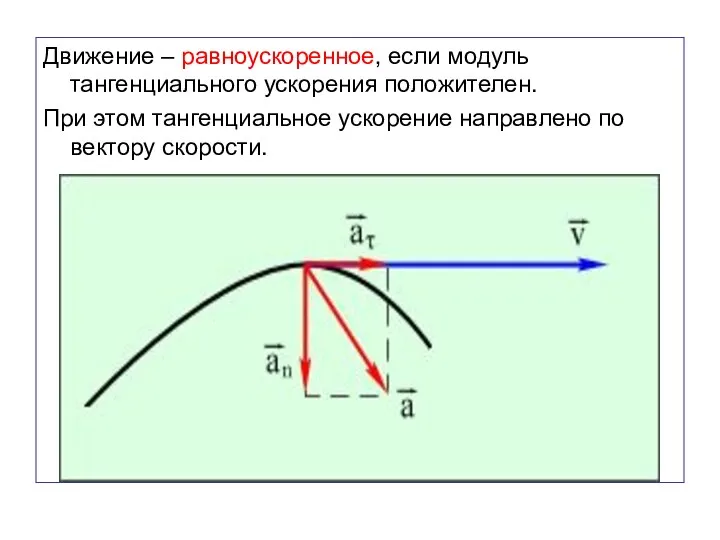
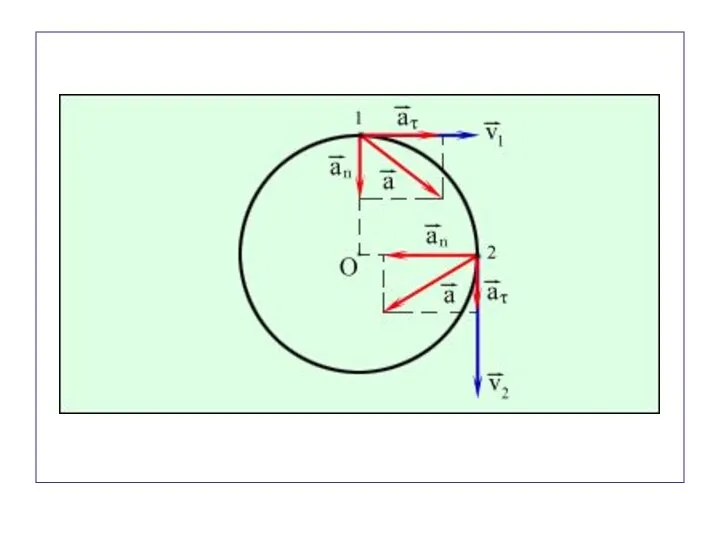
Вектор ускорения можно разложить на два направления: касательное к траектории и

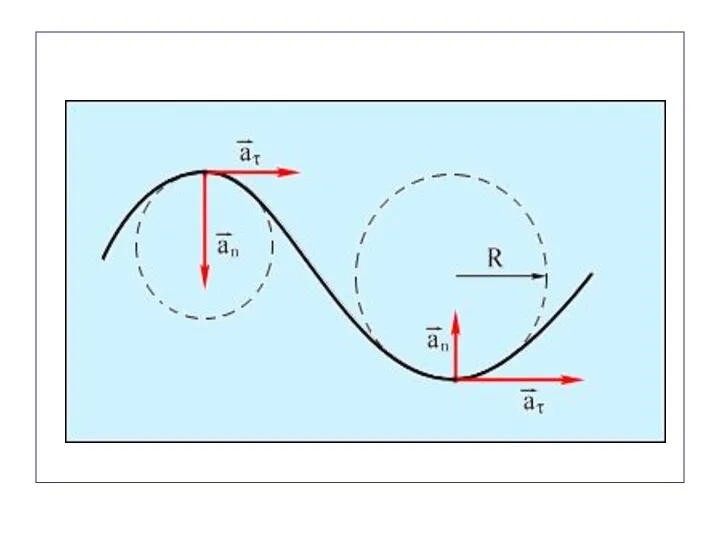
Тангенциальное ускорение характеризует изменение скорости по модулю.
Модуль тангенциального ускорения равен

Нормальное ускорение характеризует изменение скорости по направлению.
Модуль нормального ускорения равен:
Нормальное ускорение

Полное ускорение

Полное ускорение материальной точки.
Модуль полного ускорения:

Движение – равноускоренное, если модуль тангенциального ускорения положителен.
При этом тангенциальное

Частные случаи движений

= 0, = 0 - это равномерное прямолинейное

= 0, = f(t) - равномерное криволинейное движение;
5. = f(t),

1.4. Кинематика вращательного движения твердого тела

Любое движение абсолютно твердого тела может

При поступательном движении все точки тела движутся одинаково, поэтому движение тела

Вращательным движением твердого тела вокруг неподвижной оси называется такое движение, при

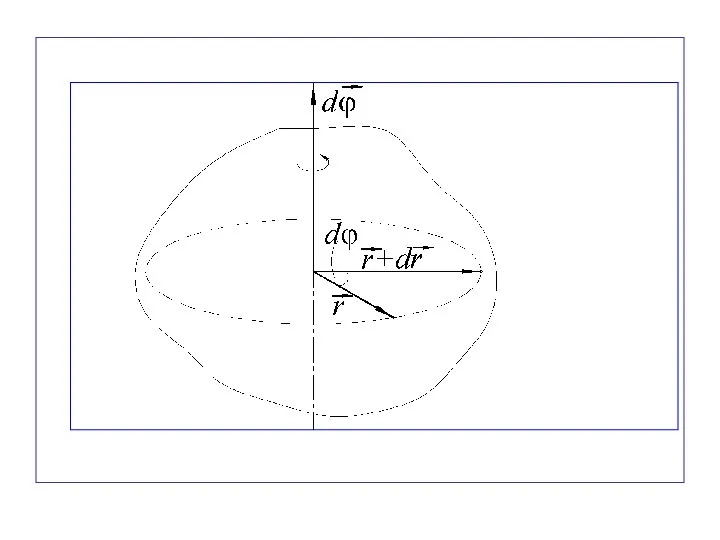
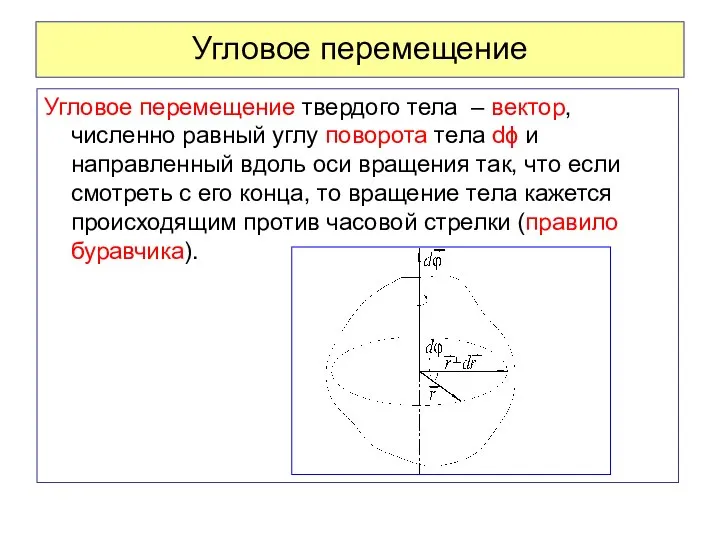
Угловое перемещение

Угловое перемещение твердого тела – вектор, численно равный углу

Быстроту изменения углового перемещения с течением времени характеризует угловая скорость.
Средняя угловая

Мгновенная угловая скорость равна первой производной от углового перемещения по времени.
Угловая

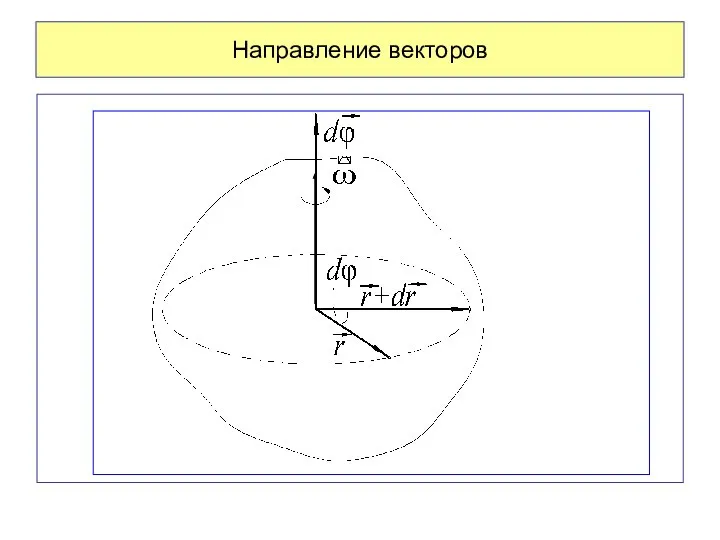
Направление векторов

Быстроту изменения угловой скорости с течением времени характеризует угловое ускорение.
Среднее угловое

Мгновенное угловое ускорение равно первой производной от угловой скорости по времени

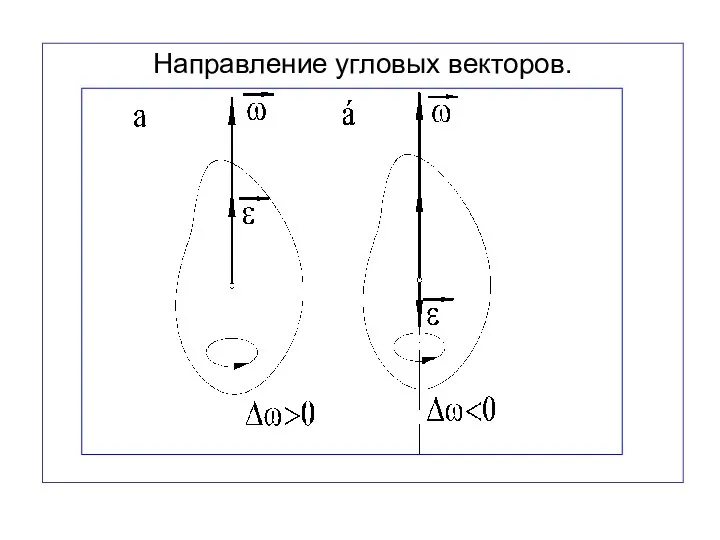
Направление угловых векторов.

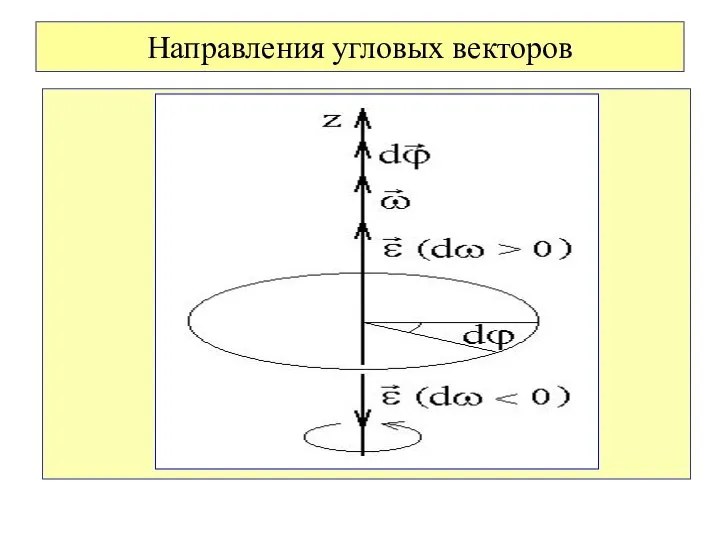
Направления угловых векторов

Вектор направлен вдоль оси вращения в ту же сторону, что

Обратная задача кинематики при вращательном движении

При вращательном движении обратная задача кинематики

При равномерном вращении:
ε = 0, ω = const, ϕ =

Период и частота вращения

Для характеристики равномерного вращательного движения используются следующие величины.
Период

1.5. Взаимосвязь угловых и линейных величин

Кроме угловых величин: углового перемещения, угловой

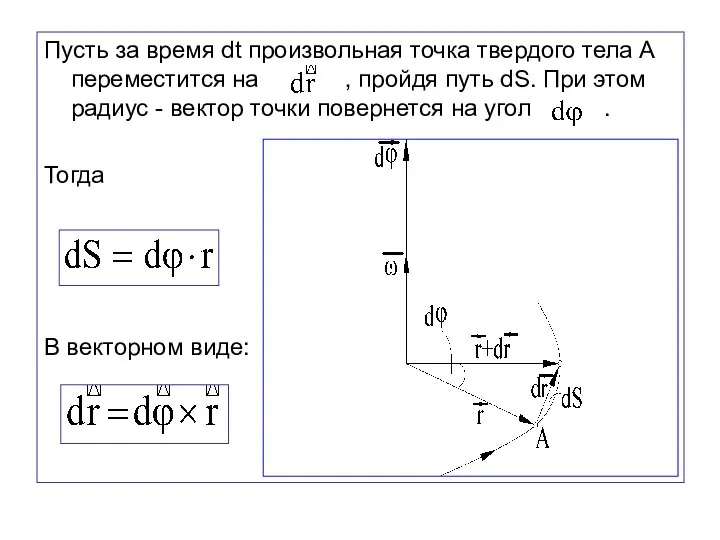
Пусть за время dt произвольная точка твердого тела А переместится на

Направление перпендикулярно к и к . Если смотреть с конца ,

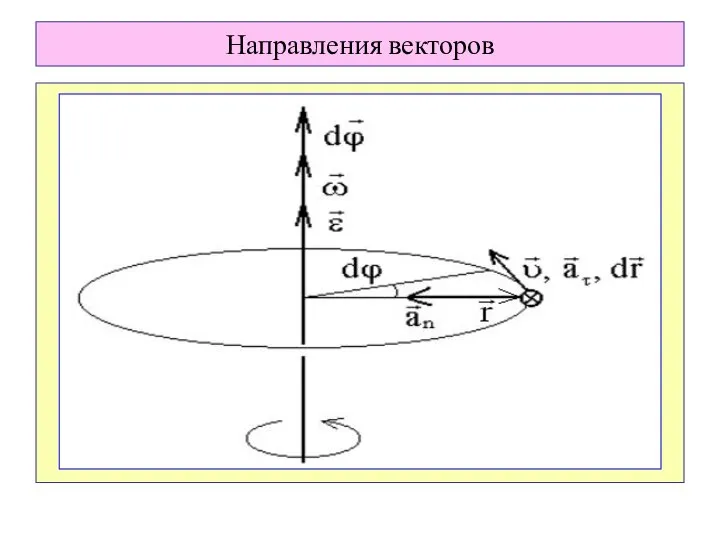
Направления векторов

Вектор элементарного перемещения:
Разделим это соотношение на dt:
Учтём, что
Получим
Линейная скорость данной

Если смотреть с конца вектора , то поворот от к происходит

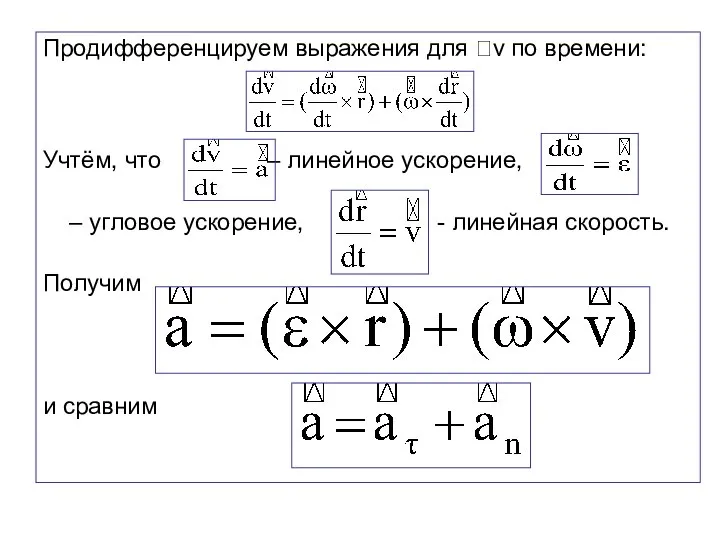
Продифференцируем выражения для v по времени:
Учтём, что – линейное ускорение,

Первый вектор в правой части - тангенциальное ускорение.
Он характеризует изменение

Второй вектор в правой части равенства – нормальное ускорение.
Оно направлено к

Сравнительная таблица формул

Движение Поступательное Вращательное
Равномерное
S = Vt ϕ = ωt