Содержание
- 2. Физические основы механики лектор: доцент кафедры физики Александр Евгеньевич Штанько Семестр 1
- 3. ЛЕКЦИЯ № 1 Кинематика материальной точки 1. Предмет физики. Физика - как основа современного естествознания. Роль
- 5. Для древних греков «физика» и «философия» были синонимами, т.к. для объяснения явлений окружающего мира использовался умозрительный
- 6. Физика изучает наиболее общие закономерности неживой природы, строение и свойства материи, законы движения материи и временной
- 7. Связные научные знания сформированы в физическую теорию - инструмент интеллектуального видения явлений материального мира. Одними из
- 8. Физика формирует материалистическое мировоззрение, лежит в основе естественно - научной подготовки инженеров, развивая критическое рациональное мышление.
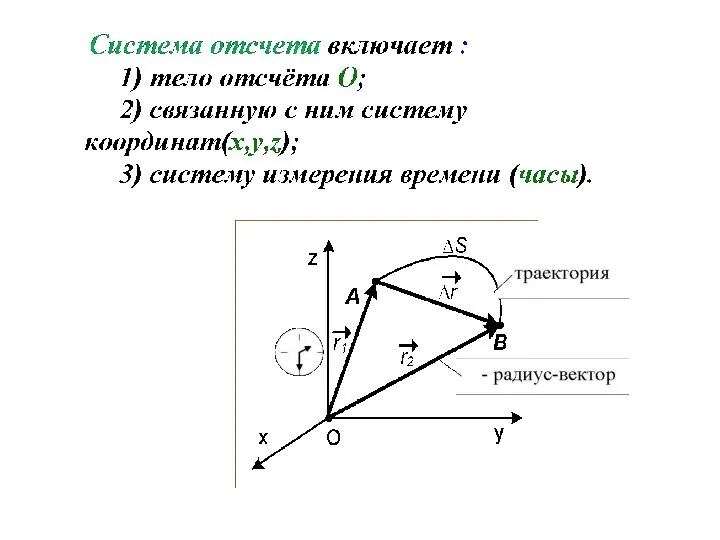
- 11. Международная система единиц СИ Законы механики устанавливают определенную связь между физическими понятиями. Большинство физических понятий имеют
- 12. Кинематика материальной точки Кинематика – раздел механики, которая описывает движение, отвлекаясь от причин, вызвавших это движение.
- 14. Материальная точка при своем движении описывает некоторую линию, которая называется траекторией. В зависимости от формы траектории
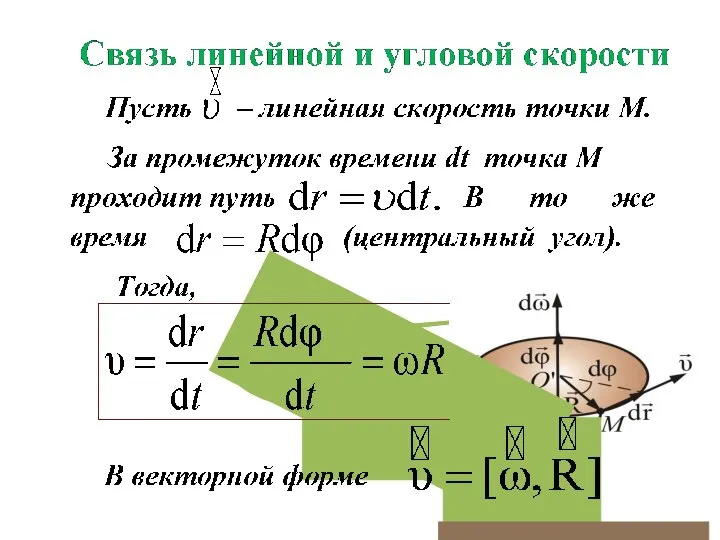
- 16. Скорость точки ( мгновенная скорость) - перемещение за малое время Вектор направлен по касательной к траектории
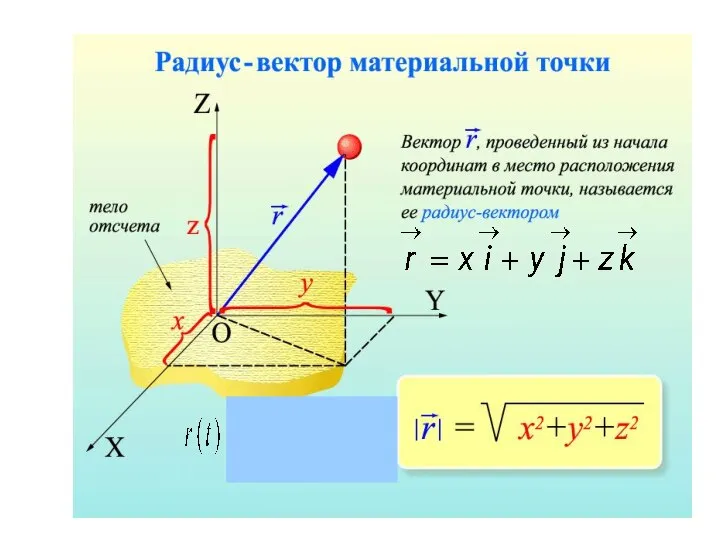
- 20. Введем единичный вектор , связанный с точкой 1 и направленный по касательной к траектории движения точки
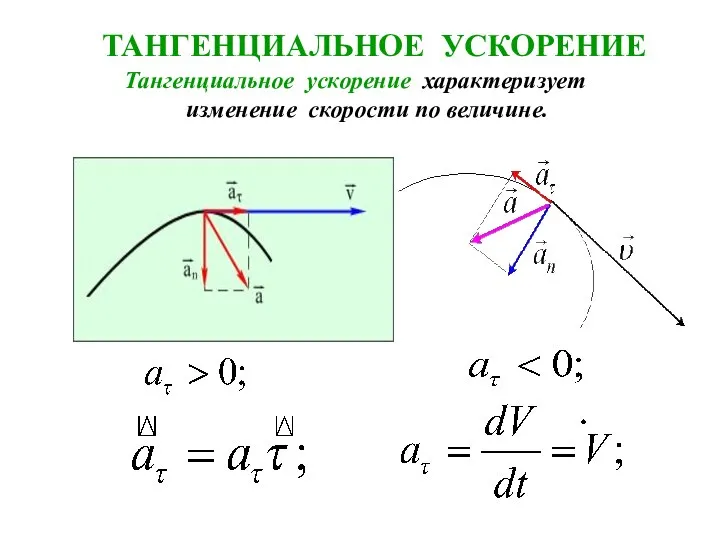
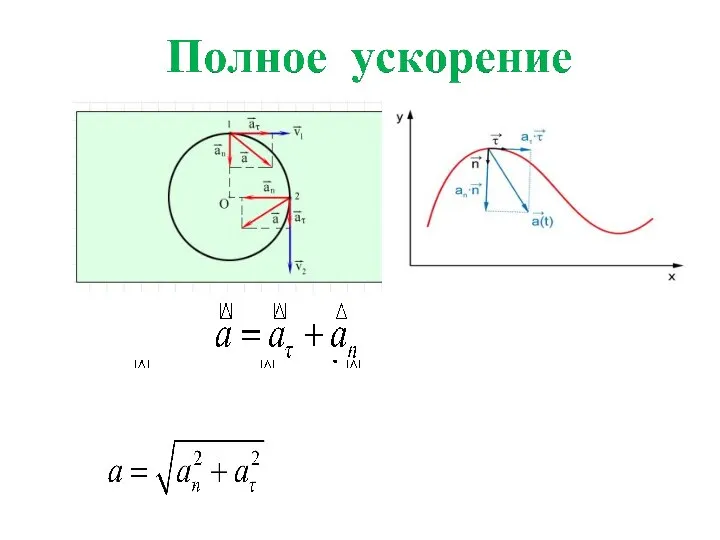
- 21. Тангенциальное ускорение характеризует изменение скорости по величине. ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ
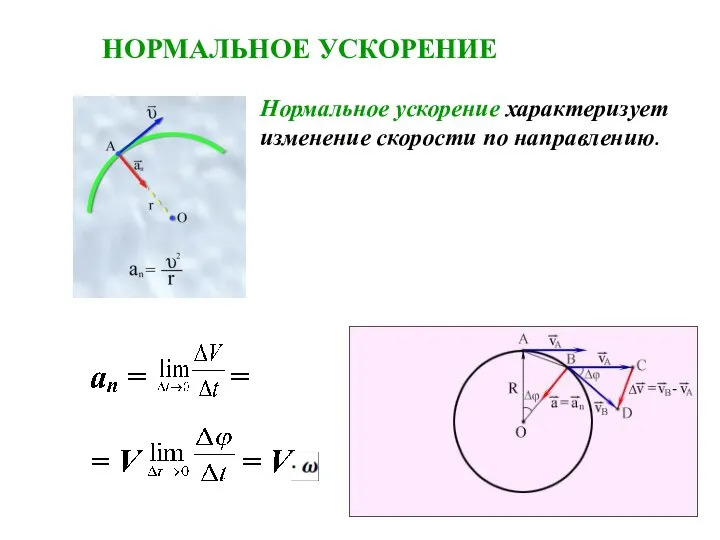
- 22. Нормальное ускорение характеризует изменение скорости по направлению. НОРМАЛЬНОЕ УСКОРЕНИЕ
- 23. Модуль нормального ускорения Нормальное ускорение или центростремительное , т.к. направлено оно к центру кривизны, перпендикулярно
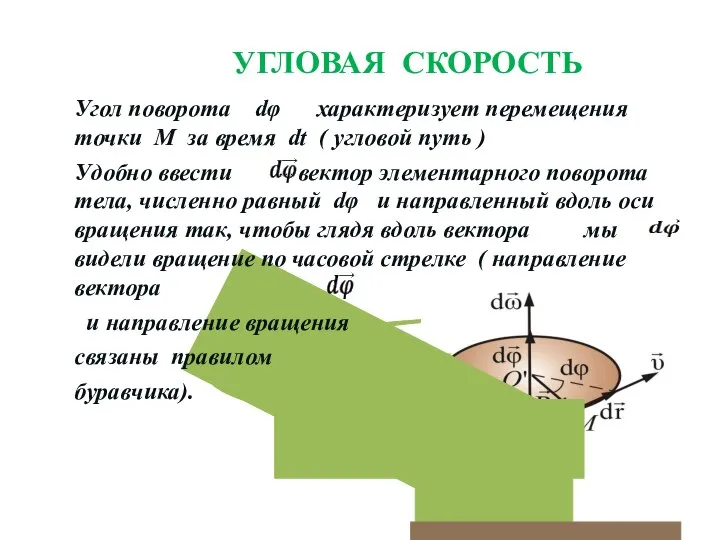
- 25. УГЛОВАЯ СКОРОСТЬ Угол поворота dφ характеризует перемещения точки М за время dt ( угловой путь )
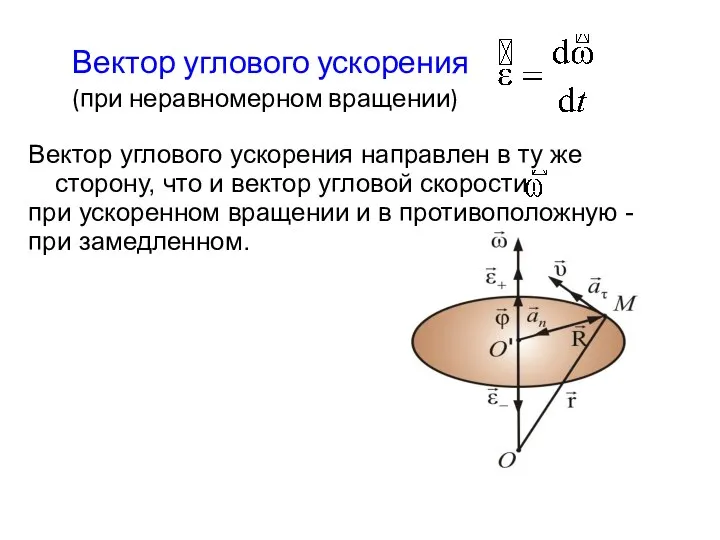
- 29. Вектор углового ускорения (при неравномерном вращении) Вектор углового ускорения направлен в ту же сторону, что и
- 31. Скачать презентацию




















 Единый государственный экзамен (ЕГЭ) – это основная форма государственной (итоговой) аттестации выпускников школ Российской Феде
Единый государственный экзамен (ЕГЭ) – это основная форма государственной (итоговой) аттестации выпускников школ Российской Феде Анализ концепции таможенного оформления и таможенного контроля товаров в местах, приближенных к государственной границе Подг
Анализ концепции таможенного оформления и таможенного контроля товаров в местах, приближенных к государственной границе Подг Особенности ВНД Общие для человека и животных
Особенности ВНД Общие для человека и животных Подтверждение статуса предпенсионера территориальными органами ПФР
Подтверждение статуса предпенсионера территориальными органами ПФР Компетентностный подход в моделировании профессиональной деятельности педагога
Компетентностный подход в моделировании профессиональной деятельности педагога Спортивный клуб КНИТУ-КАИ им. Туполева
Спортивный клуб КНИТУ-КАИ им. Туполева Презентация на тему "Как Эффективно Провести родительское собрание" - скачать презентации по Педагогике
Презентация на тему "Как Эффективно Провести родительское собрание" - скачать презентации по Педагогике Процессор Intel Core i7
Процессор Intel Core i7 Триггеры
Триггеры Команда «Аэроден-Мордовия»
Команда «Аэроден-Мордовия» Выпуклый анализ. Пространство подмножеств. Лекция 2
Выпуклый анализ. Пространство подмножеств. Лекция 2 Правописание безударных окончаний имён существительных Автор: Попружная Г.П., учитель начальных классов МОУ гимназия №8 г. Ду
Правописание безударных окончаний имён существительных Автор: Попружная Г.П., учитель начальных классов МОУ гимназия №8 г. Ду Токсические свойства, клиника, диагностика, лечения поражений фосгеном
Токсические свойства, клиника, диагностика, лечения поражений фосгеном World cup
World cup «Опыт сбора традиционных знаний в области медицины в Алайском районе Кыргызской Республики» д.м.н., профессор Карасаева А.Х.
«Опыт сбора традиционных знаний в области медицины в Алайском районе Кыргызской Республики» д.м.н., профессор Карасаева А.Х.  Основні правила гри в волейбол
Основні правила гри в волейбол Управление в здравоохранении. Управление сестринской деятельностью. Учебная практика
Управление в здравоохранении. Управление сестринской деятельностью. Учебная практика Способы включения трехфазных двигателей в однофазную сеть
Способы включения трехфазных двигателей в однофазную сеть fast-fud_-_polza_ili_vred
fast-fud_-_polza_ili_vred Организация защиты информации в системе электронного документооборота на базе платформы DocsVision
Организация защиты информации в системе электронного документооборота на базе платформы DocsVision Политическое сознание
Политическое сознание Чат-бот ВКонтакте
Чат-бот ВКонтакте Эстетика Ренессанса
Эстетика Ренессанса Возникновение и исторические этапы развития научного менеджмента
Возникновение и исторические этапы развития научного менеджмента Отопление зданий и сооружений
Отопление зданий и сооружений Курьезные дела
Курьезные дела Презентация на тему "Заболевания крови" - скачать презентации по Медицине
Презентация на тему "Заболевания крови" - скачать презентации по Медицине Использование тайм-менеджмента на Российских предприятиях
Использование тайм-менеджмента на Российских предприятиях