Содержание
- 2. 1. Способы задания движения точки 2. Скорость точки при векторном способе задания её движения 3. Скорость
- 3. Введение Кинематика Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел. Движущиеся тела рассматриваются
- 4. Система отсчёта Характер наблюдаемого движения существенно зависит от выбора тела, с которым связан наблюдатель. С твердым
- 5. Уравнения движения Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано). Задать движение
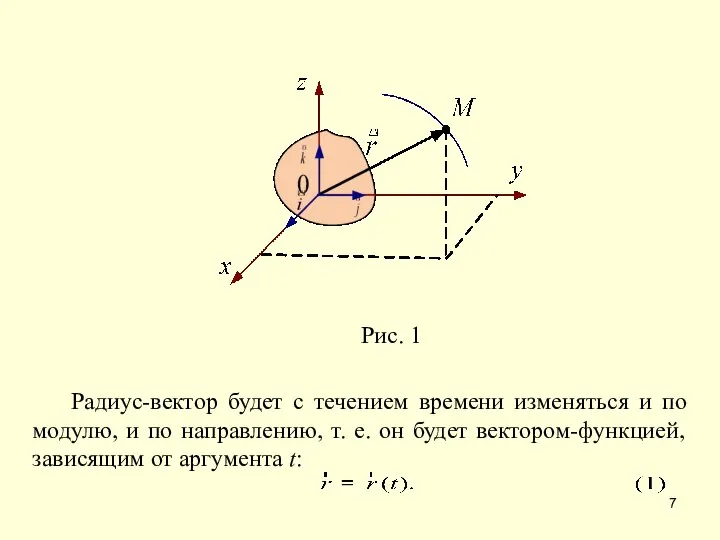
- 6. Для задания движения точки можно применять один из следующих способов: векторный, координатный, естественный. Векторный способ задания
- 8. Равенство (1) и определяет, закон движения точки в векторной форме. Непрерывная линия, которую описывает движущаяся точка
- 9. Координатный способ задания движения точки. При движении точки в пространстве её декартовы координаты х, у, z,
- 10. Уравнения (2) представляют собой уравнения движения точки в прямоугольных декартовых координатах и одновремен-но являются и уравнения
- 11. Между векторным и координатным способами движения точки существует взаимосвязь, которая заключается в следующем. Зная координаты точки
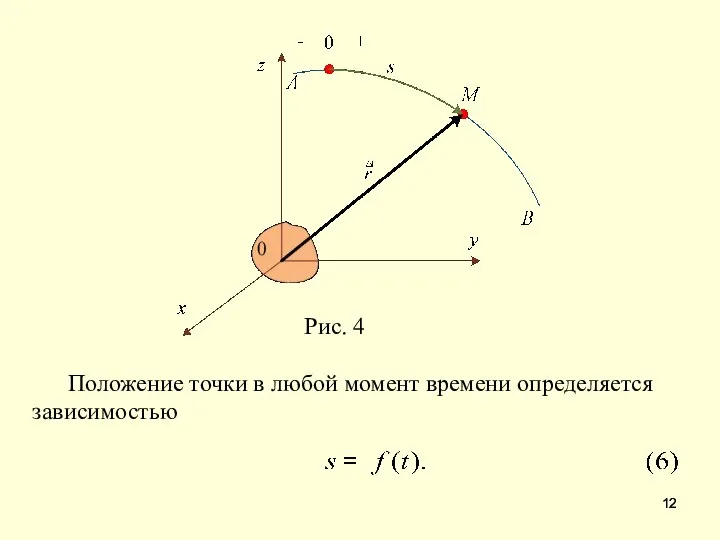
- 12. Положение точки в любой момент времени определяется зависимостью
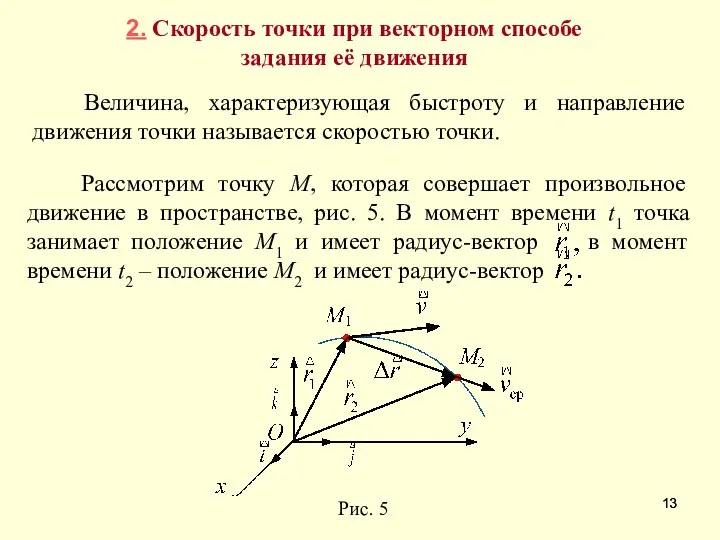
- 13. 2. Скорость точки при векторном способе задания её движения Величина, характеризующая быстроту и направление движения точки
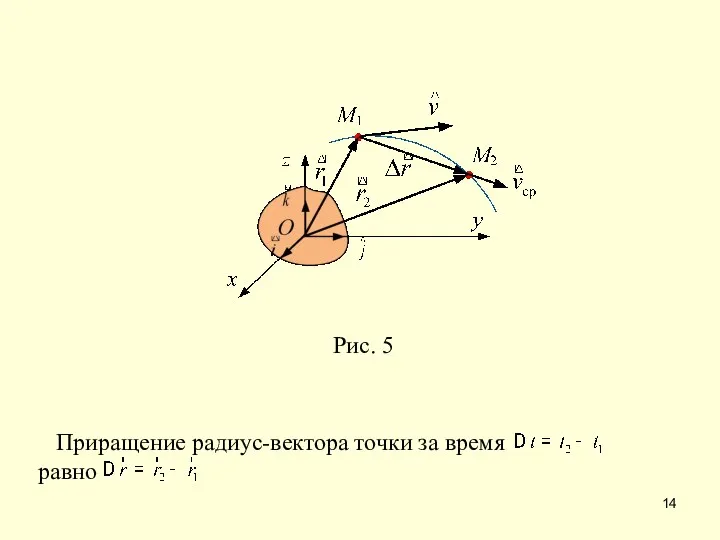
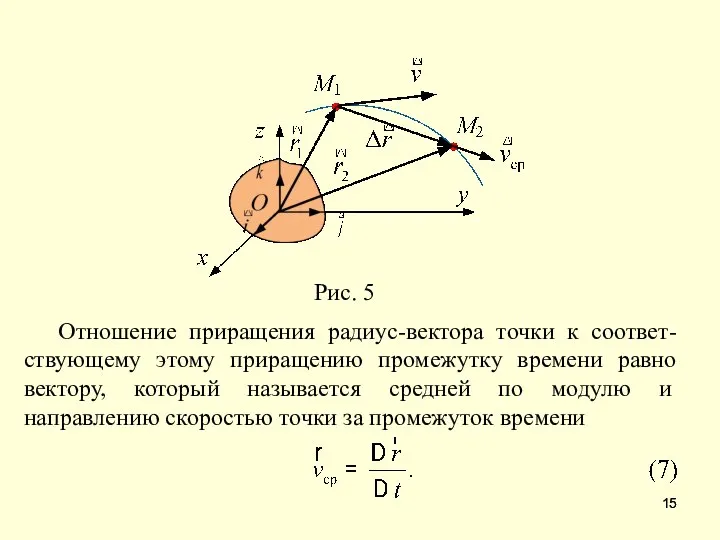
- 15. Отношение приращения радиус-вектора точки к соответ-ствующему этому приращению промежутку времени равно вектору, который называется средней по
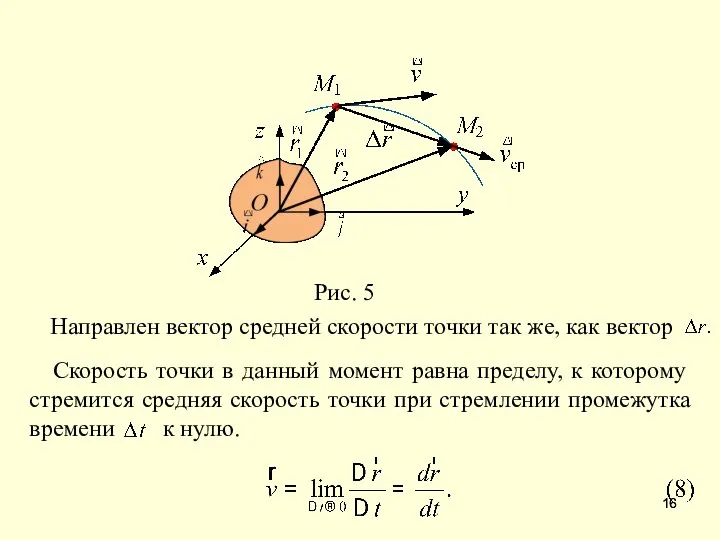
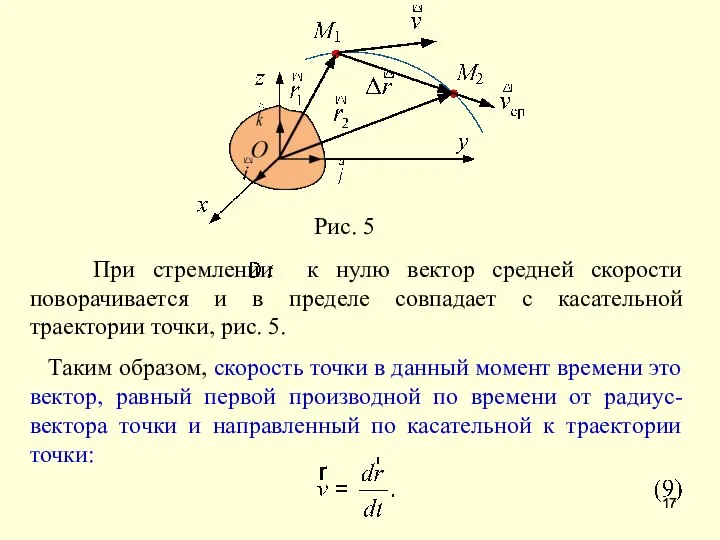
- 17. Таким образом, скорость точки в данный момент времени это вектор, равный первой производной по времени от
- 18. 3. Скорость точки при координатном способе задания её движения Радиус- вектор точки равен:
- 19. Найдём скорость точки, продифференцировав (5) по времени: Разложим вектор скорости точки по координатным осям. Сравнивая коэффициенты,
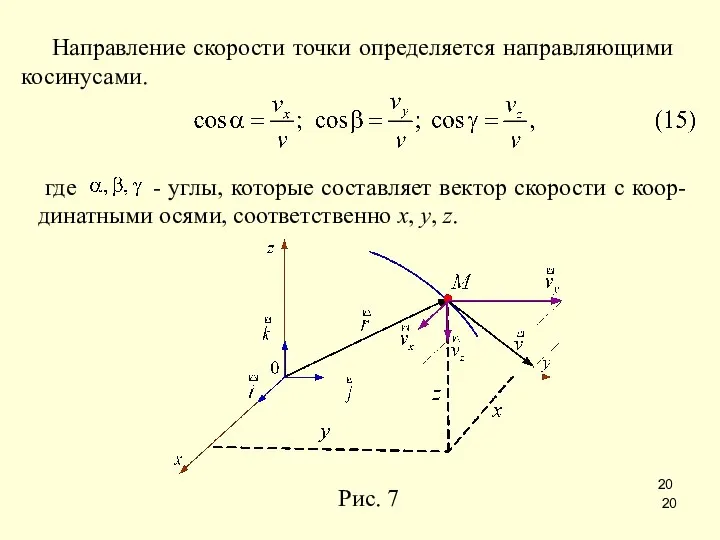
- 20. Направление скорости точки определяется направляющими косинусами.
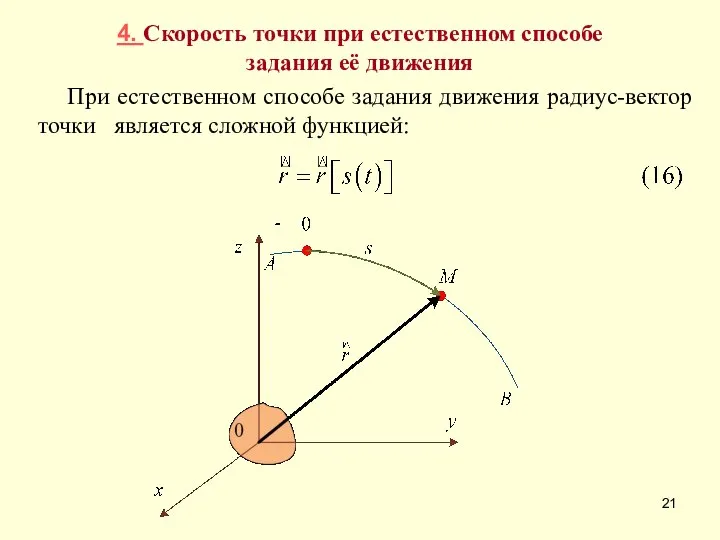
- 21. 4. Скорость точки при естественном способе задания её движения При естественном способе задания движения радиус-вектор точки
- 22. Чтобы найти скорость точки продифференцируем (16) по времени:
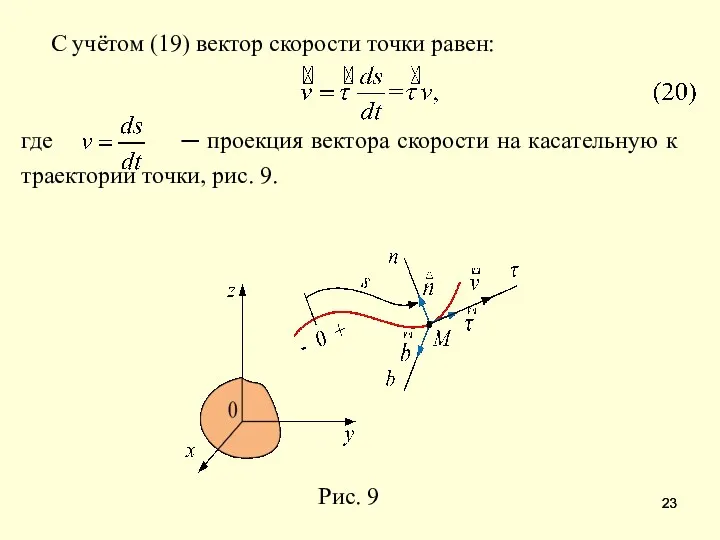
- 23. С учётом (19) вектор скорости точки равен:
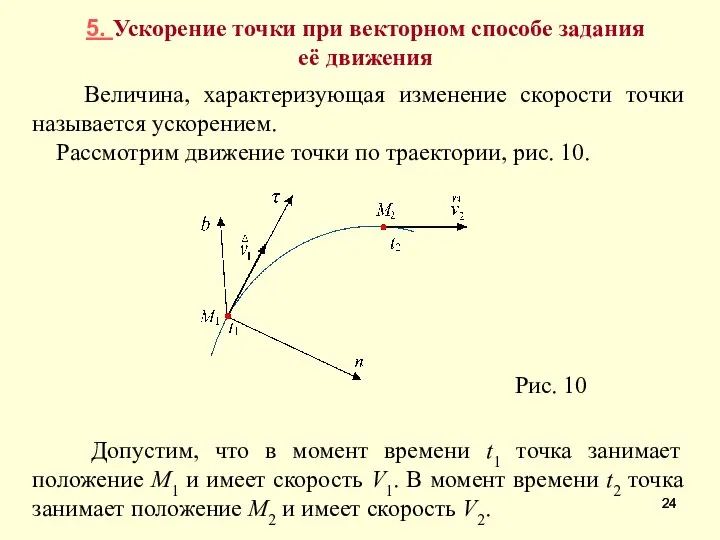
- 24. 5. Ускорение точки при векторном способе задания её движения Величина, характеризующая изменение скорости точки называется ускорением.
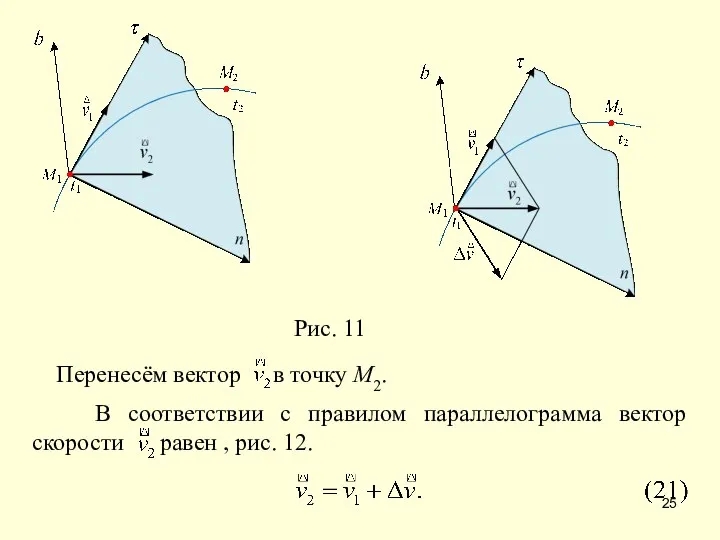
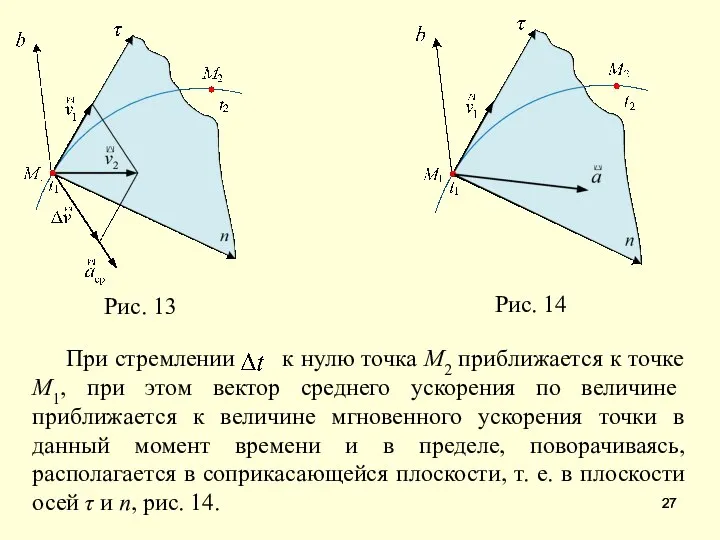
- 25. Рис. 11
- 28. Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной
- 29. Вектор скорости точки при векторном способе задания движения точки равен: В соответствии с формулой (23) 6.
- 30. Из (25) получим: С другой стороны, вектор ускорения можно разложить по координатным осям: Сравнивая в формулах
- 31. Модуль ускорения точки равен корню квадратному из суммы квадратов проекций ускорения на координатные оси: Направление вектора
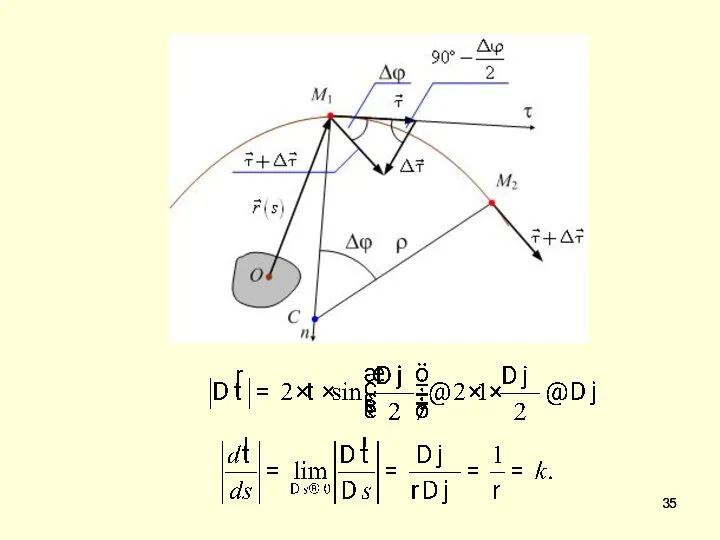
- 32. 7. Ускорение точки при естественном способе задания её движения При естественном способе задания движения вектор скорости
- 36. Таким образом производная (36) равна: Подставим производную (37) в равенство(34). Как видим, ускорение точки равно сумме
- 37. Второй вектор направлен по нормали. Его проекция на нормаль равна: Модуль вектора ускорения равен Угол μ
- 39. Скачать презентацию






















 Семейный фитнес-центр «СССР»
Семейный фитнес-центр «СССР» Презентация "Сочинение по картине Федора Александровича Васильева «Мокрый луг»" - скачать презентации по МХК
Презентация "Сочинение по картине Федора Александровича Васильева «Мокрый луг»" - скачать презентации по МХК Конструкторская документация
Конструкторская документация Цифровые технологии печати
Цифровые технологии печати Международный финансовый рынок
Международный финансовый рынок Деньги, кредит, банки
Деньги, кредит, банки  Биология в искусстве. Интеллектуальный марафон "Биологическое соцветие"
Биология в искусстве. Интеллектуальный марафон "Биологическое соцветие" Дефініція мистецтва, як відкритого поняття
Дефініція мистецтва, як відкритого поняття Система отчисления чаевых для сотрудника iPay
Система отчисления чаевых для сотрудника iPay Top Ten Culture Shocks in Korea
Top Ten Culture Shocks in Korea Культура Київської Русі
Культура Київської Русі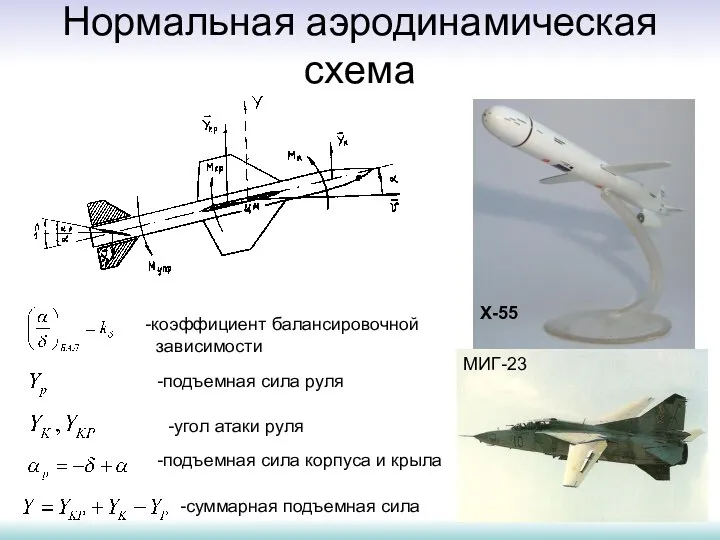 Нормальная аэродинамическая схема
Нормальная аэродинамическая схема ОЗЕРА
ОЗЕРА  kp_student
kp_student Монеты
Монеты Налог на прибыль организации
Налог на прибыль организации У краіне майстроў
У краіне майстроў RAZMINKA_05_chto_eto
RAZMINKA_05_chto_eto международный день птиц - презентация для начальной школы
международный день птиц - презентация для начальной школы Презентация на тему "Ошибки ставшие откытиями" - скачать презентации по Педагогике
Презентация на тему "Ошибки ставшие откытиями" - скачать презентации по Педагогике Марина Цветаева
Марина Цветаева Самоуправление в школе
Самоуправление в школе Презентация Дальневосточный Федеральный округ
Презентация Дальневосточный Федеральный округ Презентация "Проблемы города" - скачать презентации по Экономике
Презентация "Проблемы города" - скачать презентации по Экономике Выявление причин не включения компрессора на одной из секции электропоезда ЭТ2М
Выявление причин не включения компрессора на одной из секции электропоезда ЭТ2М Художественная культура античности. Древний Рим
Художественная культура античности. Древний Рим Иконопись. Изобразительное искусство Средневековой Руси
Иконопись. Изобразительное искусство Средневековой Руси Челси-Лестер
Челси-Лестер