Содержание
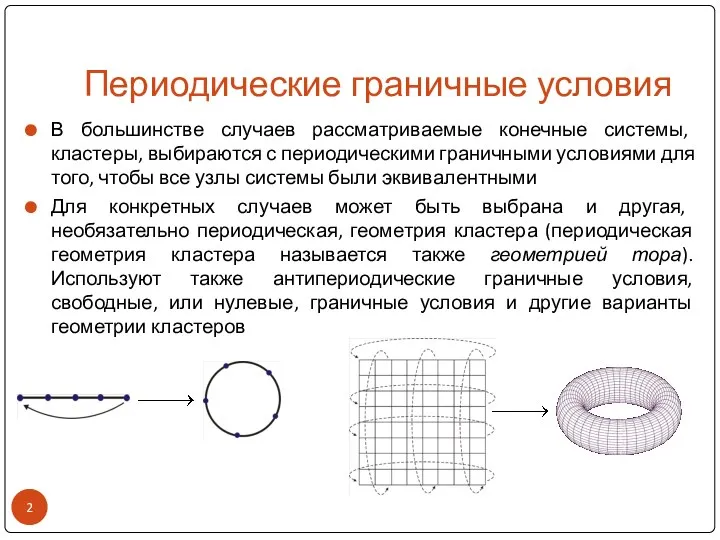
- 2. Периодические граничные условия В большинстве случаев рассматриваемые конечные системы, кластеры, выбираются с периодическими граничными условиями для
- 3. Решетка Бравэ Понизить размерность фоковского базиса системы можно, если учесть симметрию кластера Вектор трансляции на пространственной
- 4. Задача Шредингера Задача Шредингера на периодической решетке: Оператор трансляции коммутирует с гамильтонианом: Существует общая система собственных
- 5. Задача Шредингера Векторы b называются базисными векторами обратной решетки и обычно выбираются в виде: Для простой
- 6. Задача Шредингера Собственную волновую функцию гамильтониана в условиях периодического потенциала можно представить как произведение экспоненциального множителя
- 7. Пример. Одномерная цепочка Одномерная цепочка из четырех узлов с тремя частицами, описываемая моделью Бозе – Хаббарда.
- 8. Базис оператора трансляций Собственные функции оператора трансляций могут быть записаны в виде комбинаций периодической функции и
- 9. Базис оператора трансляций Матричные элементы внутри блока, отвечающего сектору m: С учетом трансляционной симметрии гамильтониана и
- 11. Скачать презентацию







 Хулиганство и вандализм - разновидности экстремизма
Хулиганство и вандализм - разновидности экстремизма Основы чир спорта
Основы чир спорта Планирование рабочего процесса. Бизнес-процессы
Планирование рабочего процесса. Бизнес-процессы Цифровизация телевидения
Цифровизация телевидения Организация С#-системы ввода-вывода
Организация С#-системы ввода-вывода Управление нововведениями в организации
Управление нововведениями в организации Основные понятия теории вероятностей, применяемые в эконометрике
Основные понятия теории вероятностей, применяемые в эконометрике Начертательная геометрия
Начертательная геометрия  Олимпийские игры в античности
Олимпийские игры в античности “Қазақстан – 2050” стратегиясы
“Қазақстан – 2050” стратегиясы Детские площадки
Детские площадки Хирург не должен сидеть в тюрьме. Особенности профессии врачей хирургических специальностей
Хирург не должен сидеть в тюрьме. Особенности профессии врачей хирургических специальностей Стопански Факултет – The Cool Way to Succeed
Стопански Факултет – The Cool Way to Succeed Лекция 5 по архитектуре компьютеров. Типы, форматы, структуры команд. Адресация
Лекция 5 по архитектуре компьютеров. Типы, форматы, структуры команд. Адресация Решение проблемы улучшения качества и количества принимаемых каналов ТВ вещания
Решение проблемы улучшения качества и количества принимаемых каналов ТВ вещания Контроль целостности Понятие хеш функции
Контроль целостности Понятие хеш функции Алгоритм методического анализа проведенного урока Н.Н.Харитонова, заместитель директора МОУ ДПОС «Учебно-методический центр»
Алгоритм методического анализа проведенного урока Н.Н.Харитонова, заместитель директора МОУ ДПОС «Учебно-методический центр» Идейно-политическое развитие стран Западной Европы
Идейно-политическое развитие стран Западной Европы «ANSAT Helicopter»
«ANSAT Helicopter» Книга и творчество Презентация к библиотечному уроку по теме «Художники-иллюстраторы» для 3 класса
Книга и творчество Презентация к библиотечному уроку по теме «Художники-иллюстраторы» для 3 класса Решение неравенств с одной переменной 8 класс - Презентация___________________________________________________________________________________________________________________
Решение неравенств с одной переменной 8 класс - Презентация___________________________________________________________________________________________________________________ Русское искусство первой трети XVIII века
Русское искусство первой трети XVIII века физкультминутка - презентация для начальной школы
физкультминутка - презентация для начальной школы ВКР: Разработка программного модуля проверки АРМ разработчика в среде Navisworks
ВКР: Разработка программного модуля проверки АРМ разработчика в среде Navisworks Роль Европейского Севера в развитии русской культуры
Роль Европейского Севера в развитии русской культуры Гибкие нейлоновые зубные протезы
Гибкие нейлоновые зубные протезы  Лекция 3 часть 2
Лекция 3 часть 2 Подпрограммы (язык C, лекция 7)
Подпрограммы (язык C, лекция 7)