Содержание
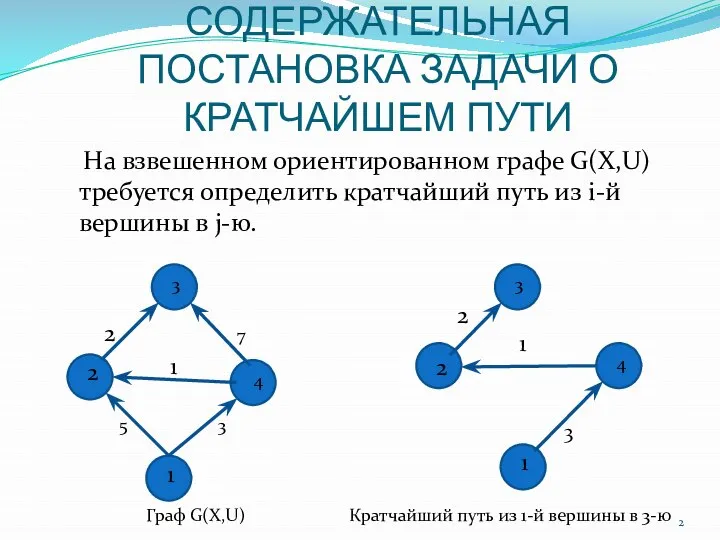
- 2. СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ О КРАТЧАЙШЕМ ПУТИ На взвешенном ориентированном графе G(X,U) требуется определить кратчайший путь из
- 3. ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ О КРАТЧАЙШЕМ ПУТИ Поиск кратчайшего пути из s-й вершины в t-ю
- 4. МЕТОД ПОТЕНЦИАЛОВ Шаг 1. Вершине присваивается потенциал P(s)=0. Шаг 2. Всем вершинам множества Х\ присвоить потенциал,
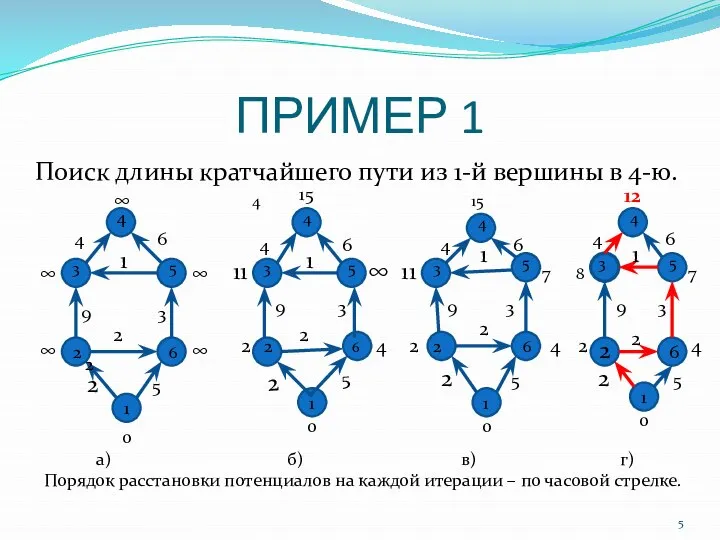
- 5. ПРИМЕР 1 Поиск длины кратчайшего пути из 1-й вершины в 4-ю. 1 2 3 4 5
- 6. ДОСТОИНСТВА И НЕДОСТАТКИ Достоинства: Метод потенциалов гарантирует определение кратчайших путей из выбранной вершины во все остальные.
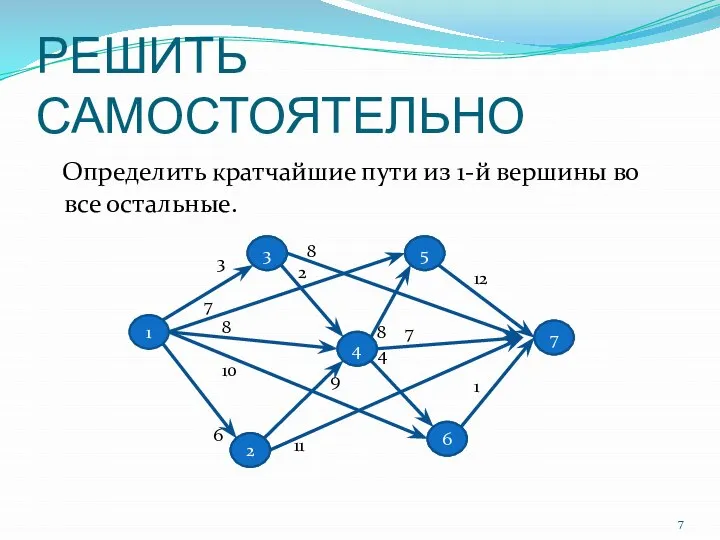
- 7. РЕШИТЬ САМОСТОЯТЕЛЬНО Определить кратчайшие пути из 1-й вершины во все остальные. 1 3 7 8 10
- 8. МАКСИМАЛЬНЫЕ ПОТОКИ НА ГРАФАХ Содержательная постановка задачи: требуется определить максимальный однородный поток на графе G(X,U) из
- 9. Формальная постановка задачи о максимальном однородном потоке Обозначения: f(i,j) – поток по дуге , r(i,j) –
- 10. САМОСТОЯТЕЛЬНО Дайте иную формальную постановку задачи о максимальном потоке, в которой: эмиссионная способность источника ограничена; поглощающая
- 11. ЧАСТО ИСПОЛЬЗУЕМЫЙ АЛГОРИТМ ПОИСКА МАКСИМАЛЬНОГО ПОТОКА Шаг 1. Полученный граф G(X,U’) заменяется на G’(X,U’) такой, что:
- 12. АЛГОРИТМ ПОИСКА МАКСИМАЛЬНОГО ПОТОКА (ПРОДОЛЖЕНИЕ) Шаг 5. На графе G(X,U) вес всех дуг, принадлежавших пути L,
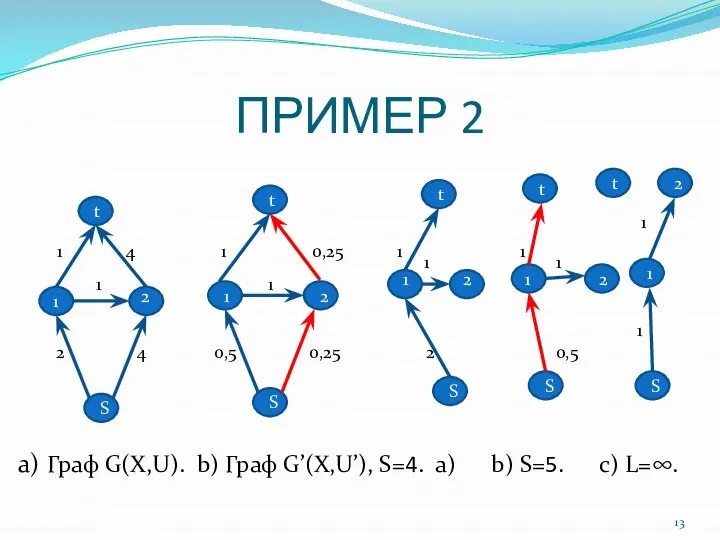
- 13. ПРИМЕР 2 a) Граф G(X,U). b) Граф G’(X,U’), S=4. a) b) S=5. c) L=∞. 1 S
- 14. САМОСТОЯТЕЛЬНО Сформулируйте достоинства приведенного выше алгоритма. Сформулируйте недостатки приведенного выше алгоритма.
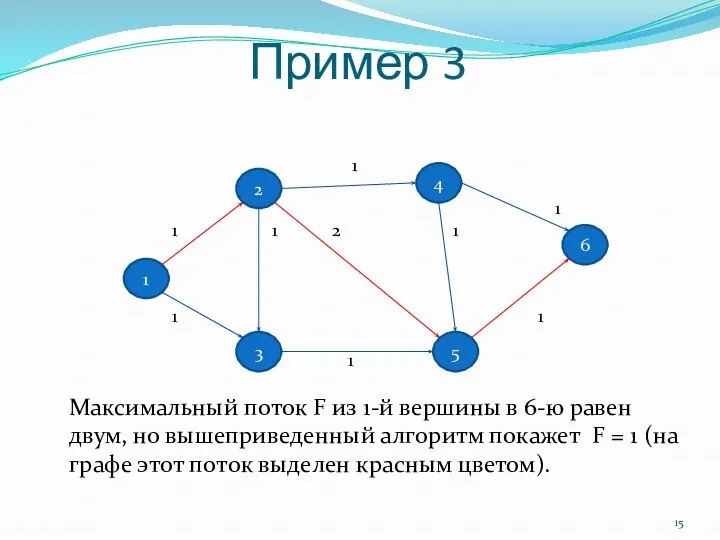
- 15. Пример 3 1 4 3 2 6 5 1 1 1 1 2 1 1 1
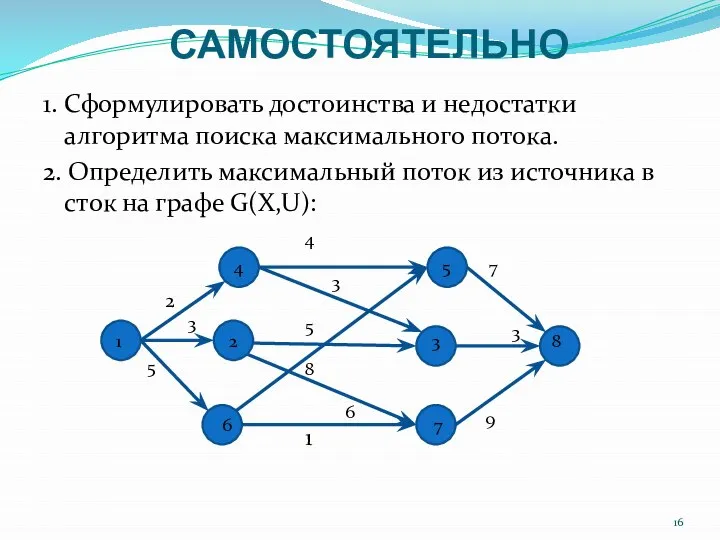
- 16. САМОСТОЯТЕЛЬНО 1. Сформулировать достоинства и недостатки алгоритма поиска максимального потока. 2. Определить максимальный поток из источника
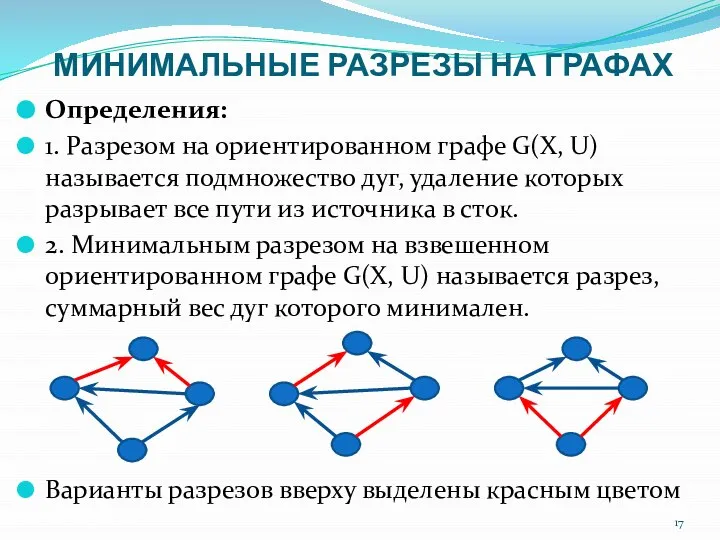
- 17. МИНИМАЛЬНЫЕ РАЗРЕЗЫ НА ГРАФАХ Определения: 1. Разрезом на ориентированном графе G(X, U) называется подмножество дуг, удаление
- 18. Обозначения и определения Z(i,j) – булева переменная, равная единице, если дуга (i,j) принадлежит минимальному разрезу и
- 19. Формальная постановка задачи о минимальном разрезе
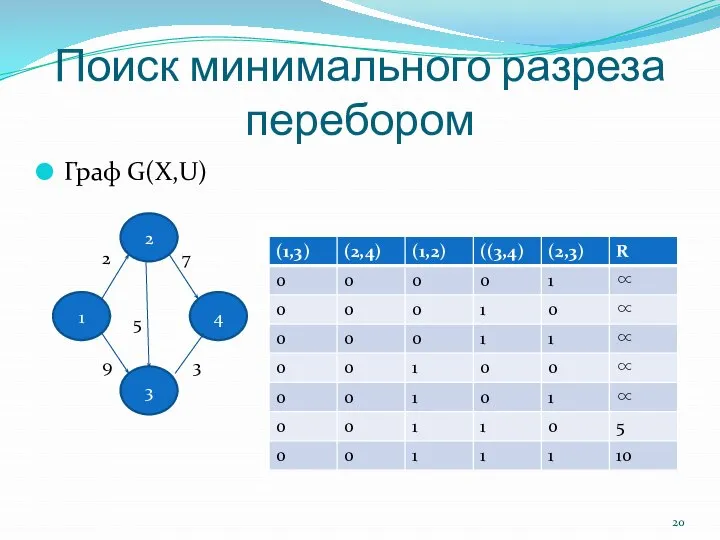
- 20. Поиск минимального разреза перебором Граф G(X,U) 1 4 3 2 2 7 5 9 3
- 21. ТЕОРЕМА ФОРДА-ФАЛКЕРСОНА Величина минимального разреза на взвешенном ориентированном графе равна величине максимального потока.
- 23. Скачать презентацию












 «Нет ничего лучше «Нет ничего лучше Невского проспекта…»
«Нет ничего лучше «Нет ничего лучше Невского проспекта…» Презентация Население в международном праве
Презентация Население в международном праве  принципы и направления развития таможенных органов Выполнили Студентки 1-го курса ФТД Врублевская Мария и ЗахаренкоОльга.
принципы и направления развития таможенных органов Выполнили Студентки 1-го курса ФТД Врублевская Мария и ЗахаренкоОльга. Никола́й Ива́нович Лобаче́вский (1793-1856) - русский математик, создатель неевклидовой геометрии
Никола́й Ива́нович Лобаче́вский (1793-1856) - русский математик, создатель неевклидовой геометрии Introduction and Operation for Changan Scanner KT660
Introduction and Operation for Changan Scanner KT660 Профессия инженер-программист
Профессия инженер-программист Республиканская конференция «Отечественные франшизы, как фактор роста казахстанского содержания» 31.01.2012г. «КАЗАХСТАНСКОЕ С
Республиканская конференция «Отечественные франшизы, как фактор роста казахстанского содержания» 31.01.2012г. «КАЗАХСТАНСКОЕ С КРИПТОГРАФИЯ С ОТКРЫТЫМ КЛЮЧОМ
КРИПТОГРАФИЯ С ОТКРЫТЫМ КЛЮЧОМ  Учебно-демонстрационный стенд «Астра-Дозор». Система охранной сигнализации
Учебно-демонстрационный стенд «Астра-Дозор». Система охранной сигнализации TrischiniZmitsnennya.ppt
TrischiniZmitsnennya.ppt English grammar
English grammar Правовое обеспечение местного самоуправления. Лекция 4
Правовое обеспечение местного самоуправления. Лекция 4 Микропроцессоры. Логические основы ЭВМ, элементы и узлы
Микропроцессоры. Логические основы ЭВМ, элементы и узлы Михаил Васильевич Фрунзе
Михаил Васильевич Фрунзе Сфера духовной культуры
Сфера духовной культуры Древо целей и задач города Брянска Подготовили студенты ФТД группы Т-115 Майстренко Денис.и Рассоленко Артём
Древо целей и задач города Брянска Подготовили студенты ФТД группы Т-115 Майстренко Денис.и Рассоленко Артём Презентация Iura in re aliena, их понятие, классификация. Парциарные вещные права как res incorporales. Классификация сервитутов по Марциану
Презентация Iura in re aliena, их понятие, классификация. Парциарные вещные права как res incorporales. Классификация сервитутов по Марциану ПОДЛЕЖАЩЕЕ Подлежащее — главный член предложения, который отвечает на вопросы именительного падежа кто? что?
ПОДЛЕЖАЩЕЕ Подлежащее — главный член предложения, который отвечает на вопросы именительного падежа кто? что? РОССИЙСКАЯ СИМВОЛИКА
РОССИЙСКАЯ СИМВОЛИКА Влагомаслоотделитель пневматической системы троллейбуса ЗИУ - 9
Влагомаслоотделитель пневматической системы троллейбуса ЗИУ - 9 Политические системы и режимы
Политические системы и режимы Деревня - деревянный мир
Деревня - деревянный мир У солнышка в гостях
У солнышка в гостях  Площади помещений детских дошкольных учреждений
Площади помещений детских дошкольных учреждений Политическая элита, лидеры, партии
Политическая элита, лидеры, партии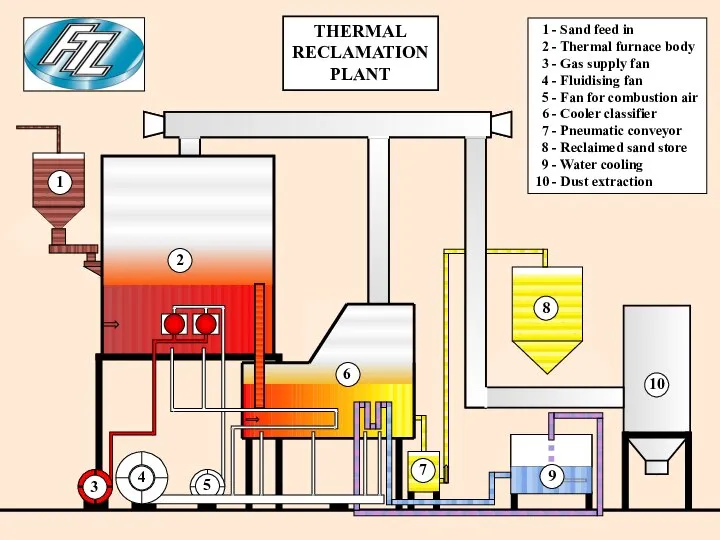 Thermal reclamation plant
Thermal reclamation plant Компьютерное моделирование артикуляторных и акустических процессов в естественных языков
Компьютерное моделирование артикуляторных и акустических процессов в естественных языков Презентация "Структура экономики (хозяйства)" - скачать презентации по Экономике
Презентация "Структура экономики (хозяйства)" - скачать презентации по Экономике