Содержание
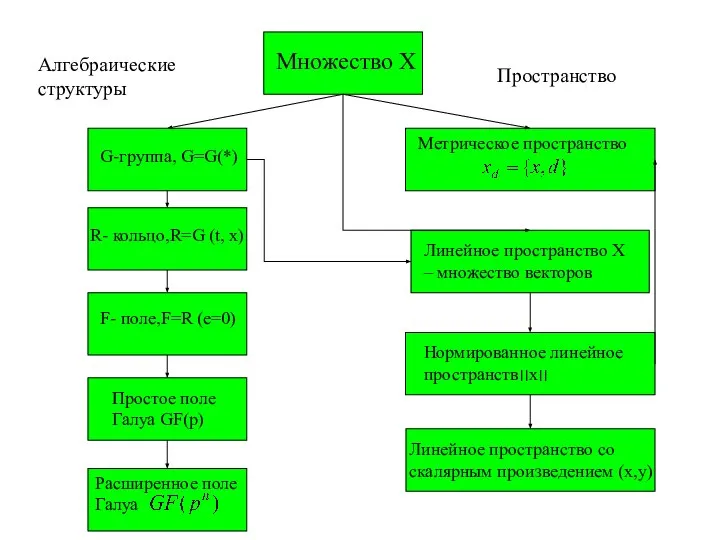
- 2. Множество Х Алгебраические структуры Пространство G-группа, G=G(*) R- кольцо,R=G (t, x) F- поле,F=R (e=0) Простое поле
- 3. Группа Определение 1: Множество G называется группой относительно бинарной операции (*), если выполняются следующие свойства: 1)Замкнутость:
- 4. Примечание: Если элементы группы обладают коммутативным свойством: α,β G; α*β = β*α, то такая группа называется
- 5. 2. Множество мнимых чисел X=J * - сложение 1),2),3) е=0,4) -выполняются, Значит X=J является группой. 3.
- 6. Подгруппа Определение 2: Подмножество G0 группы G обладающее свойствами группы называется подгруппой Пример: G0 = {000,001,010,011}
- 7. Кольцо Определение 3:Множество R являющееся группой относительно бинарной операции сложения называется кольцом, если относительно операции умножения
- 8. Примеры: Множество вещественных чисел R. Множество многочленов A(x) c коэффициентами из R.
- 9. Поле F Определение 4: Кольцо F называется полем, если относительно бинарной операции умножения этого кольца, выполняются
- 10. Простое поле Галуа Определение 5: Множество целых чисел GF(p):{0,1,2,…,р-1} образует простое поле Галуа относительно бинарной операции
- 11. a b = c = a · b = d = Пример: р=7- модуль GF(p) ={0,1,2,3,4,5,6}
- 12. Модулярный многочлен(ММ) Определение 6: Многочлен называется модулярным, если коэф-ты этого многочлена принадлежат простому полю Галуа, причем
- 13. Неприводимый ММ Определение 7: Многочлен М(х) степени n, с коэф-ми из простого поля Галуа называется неприводимым
- 15. Скачать презентацию








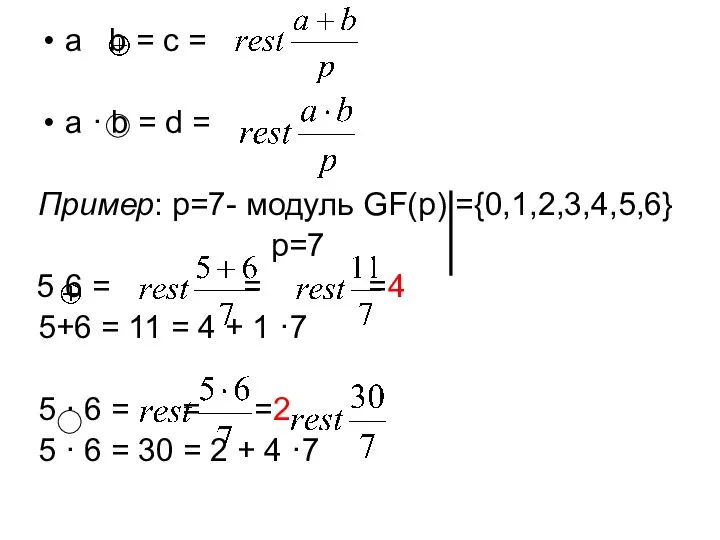


 Урок математики Образование десятка.
Урок математики Образование десятка. Одежда мусульманина
Одежда мусульманина Федеральный закон РФ о наркотических средствах и психотропных веществах
Федеральный закон РФ о наркотических средствах и психотропных веществах Христианская семья и ее ценности
Христианская семья и ее ценности Русские драматурги 18 – начало 20 века
Русские драматурги 18 – начало 20 века Олимпийские игры
Олимпийские игры Аппаратные средства визуализации
Аппаратные средства визуализации Пути улучшения экологической ситуации в Крыму
Пути улучшения экологической ситуации в Крыму  Поверить в Иисуса значит принять мудрость, любовь бога и людей
Поверить в Иисуса значит принять мудрость, любовь бога и людей Сведения о СРО «Свободный Оценочный Департамент» и ответственность оценщиков за не соблюдение правил профессиональной этики
Сведения о СРО «Свободный Оценочный Департамент» и ответственность оценщиков за не соблюдение правил профессиональной этики Недостаточность кровообращения
Недостаточность кровообращения Курсы по выбору – основа предпрофильной подготовки школьников
Курсы по выбору – основа предпрофильной подготовки школьников Формирование государства на Руси. Русь Феодальная IX- начала XVII вв.
Формирование государства на Руси. Русь Феодальная IX- начала XVII вв. Теоретические основы документальных БД. Теоретико-множественная модель индексирования и поиска.
Теоретические основы документальных БД. Теоретико-множественная модель индексирования и поиска.  Понятие «демократия». Многозначность подходов
Понятие «демократия». Многозначность подходов Математические модели и методы теории систем массового обслуживания, используемые в САПР КЭС. Лекция 4
Математические модели и методы теории систем массового обслуживания, используемые в САПР КЭС. Лекция 4 Общие вопросы технологии программирования (Лекция 1)
Общие вопросы технологии программирования (Лекция 1) Сюрреализм. История развития
Сюрреализм. История развития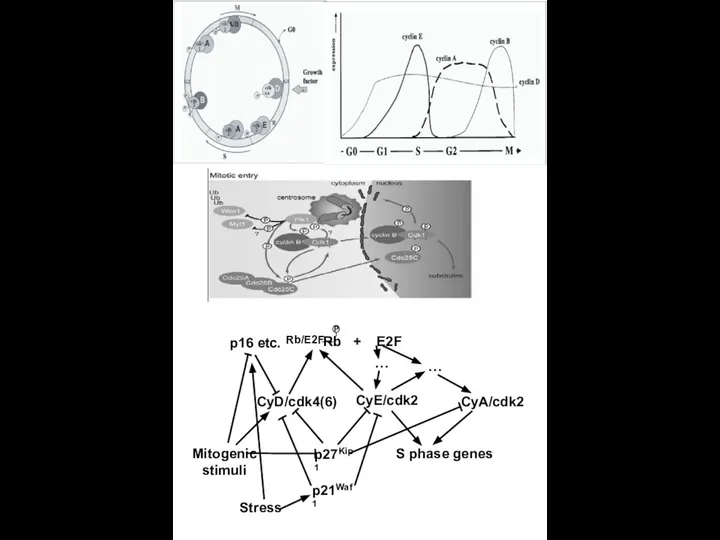 Cell cycle
Cell cycle Определение твёрдости металлов и сплавов
Определение твёрдости металлов и сплавов Хеш функції
Хеш функції DeVita Energy mini - цифровое устройство оздоровления
DeVita Energy mini - цифровое устройство оздоровления Совершенствование профессиональной деятельности на основе ее психологической составляющей
Совершенствование профессиональной деятельности на основе ее психологической составляющей  Живопись эпохи мезолита Пиктограмма
Живопись эпохи мезолита Пиктограмма  Реестр контрактов_ВКС_9.3.
Реестр контрактов_ВКС_9.3. Массовые туристские соревнования школьников
Массовые туристские соревнования школьников Зимняя Олимпиада в Сочи 2014 год
Зимняя Олимпиада в Сочи 2014 год ОСВ-1. Принципы, параметры, значение
ОСВ-1. Принципы, параметры, значение