Содержание
- 2. Вектор состояния 〈 D | S 〉 = 〈 D | 1 〉⋅〈 1 | S
- 3. Правило 1 амплитуда вероятности любого события (квантового перехода) всегда может быть представлена в виде скалярного произведения
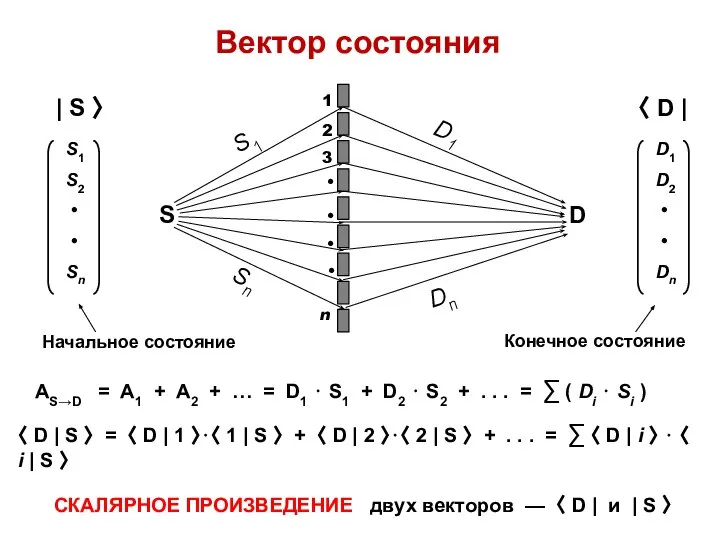
- 4. | S 〉 = S1 ⋅ | 1 〉 + S2 ⋅ | 2 〉 +
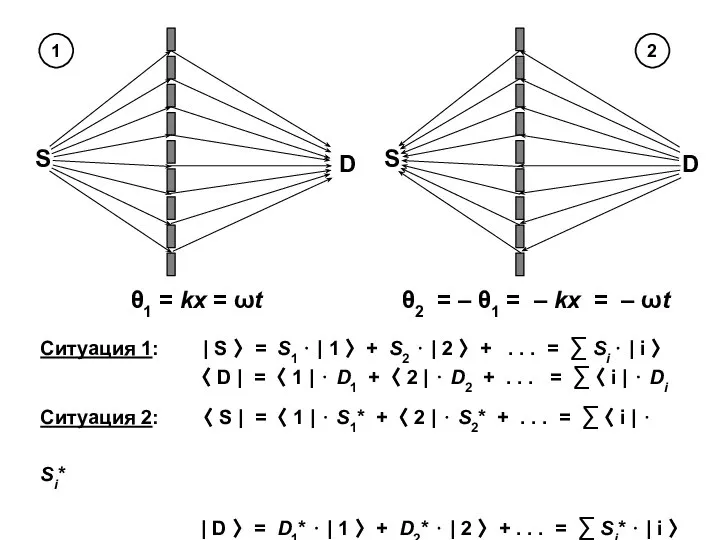
- 5. θ1 = kx = ωt θ2 = – θ1 = – kx = – ωt Ситуация
- 6. Правило 3 каждое состояние можно представить двумя экземплярами вектора состояния, которые являются ЭРМИТОВО СОПРЯЖЕННЫМИ относительно друг
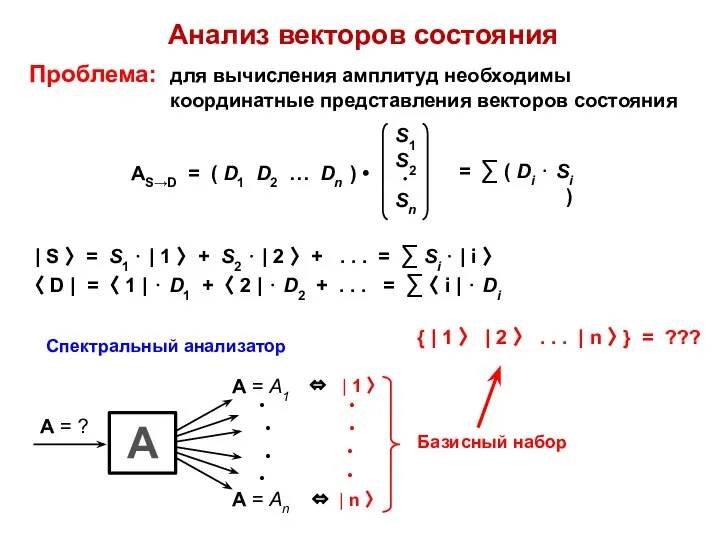
- 7. Анализ векторов состояния Проблема: для вычисления амплитуд необходимы координатные представления векторов состояния | S 〉 =
- 8. Правило 4 любое базисное состояние является собственным для некоторого спектрального анализатора ( А ), т.е. для
- 9. Прибор А: | Ψ 〉А = а1 ⋅ | А1 〉 + а2 ⋅ | А2
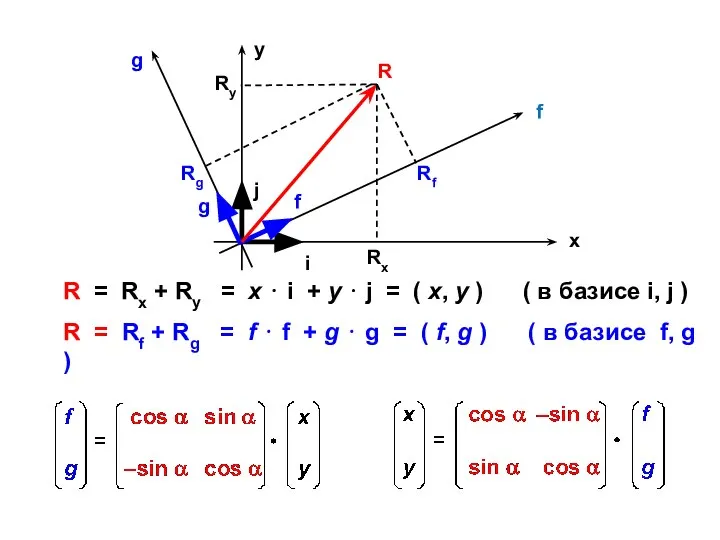
- 10. x y f g i j f g R Rx Ry Rg Rf R = Rx
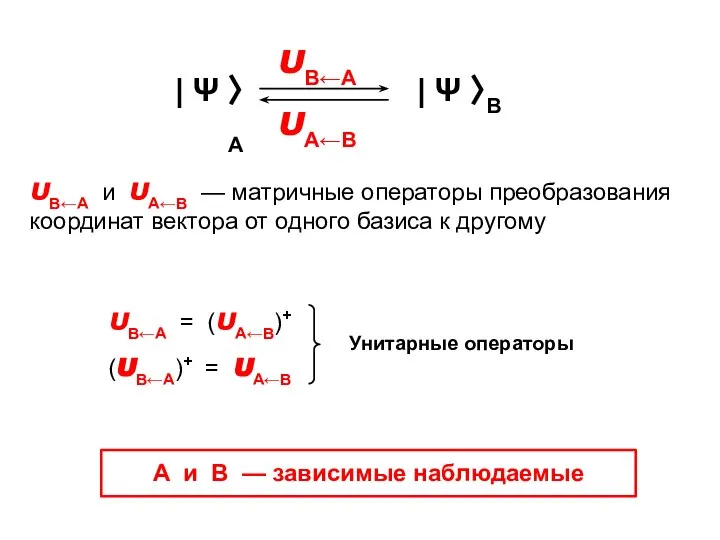
- 11. UB←A и UA←B — матричные операторы преобразования координат вектора от одного базиса к другому А и
- 12. Независимые наблюдаемые Прибор А: | Ψ 〉А = а1 ⋅ | А1 〉 + а2 ⋅
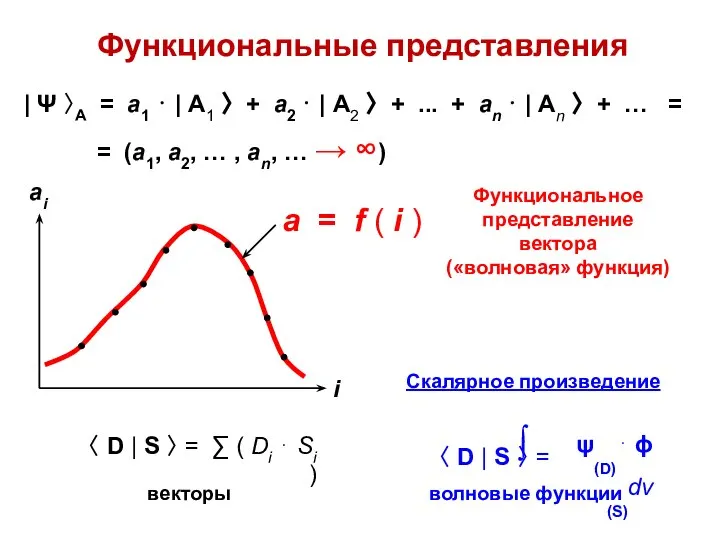
- 13. Функциональные представления | Ψ 〉А = а1 ⋅ | А1 〉 + а2 ⋅ | А2
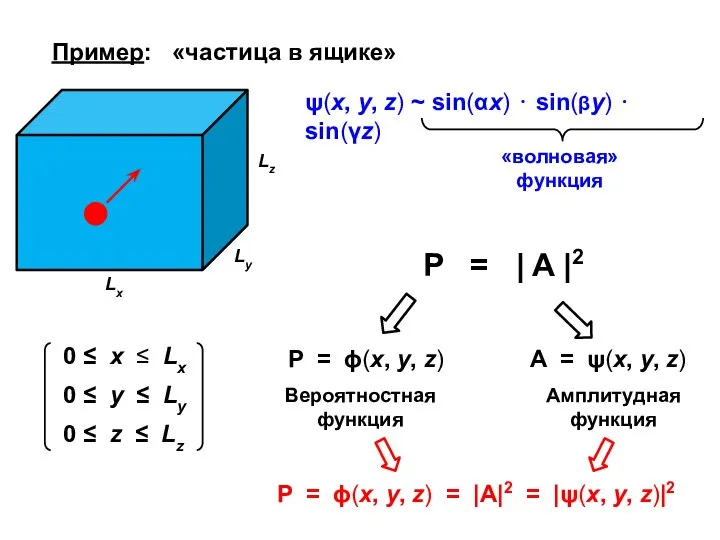
- 14. Пример: «частица в ящике» P = | A |2 ψ(x, y, z) ~ sin(αx) ⋅ sin(βy)
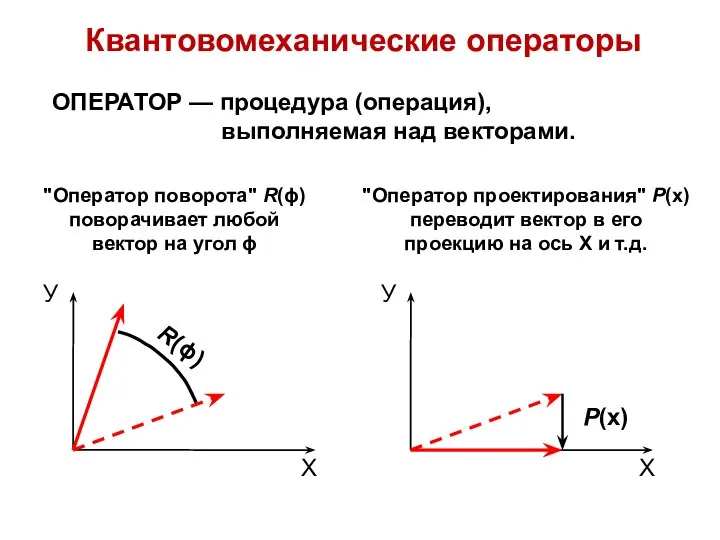
- 15. Квантовомеханические операторы ОПЕРАТОР — процедура (операция), выполняемая над векторами.
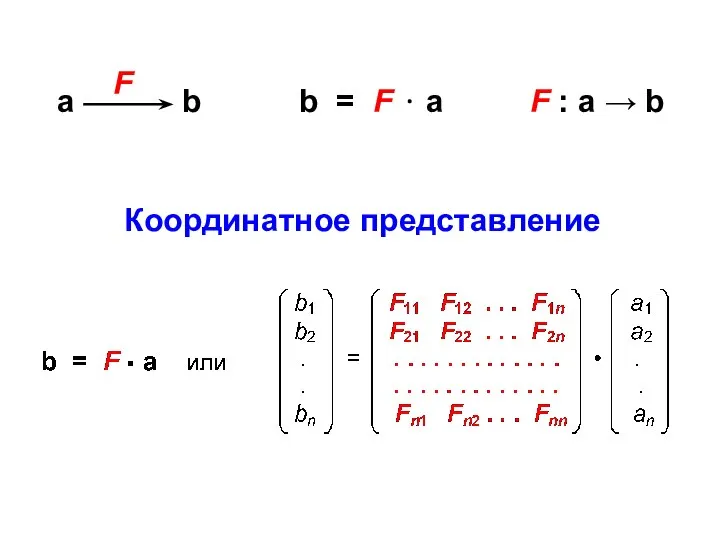
- 16. b = F ⋅ a F : a → b Координатное представление
- 17. Функциональное представление
- 18. Явный вид оператора зависит от использованного базиса b = F • a 1-й базис ( b
- 19. U12 = (U21)–1 = (U21)+ U21 = (U12)–1 = (U12)+ Связь между представлениями оператора F (
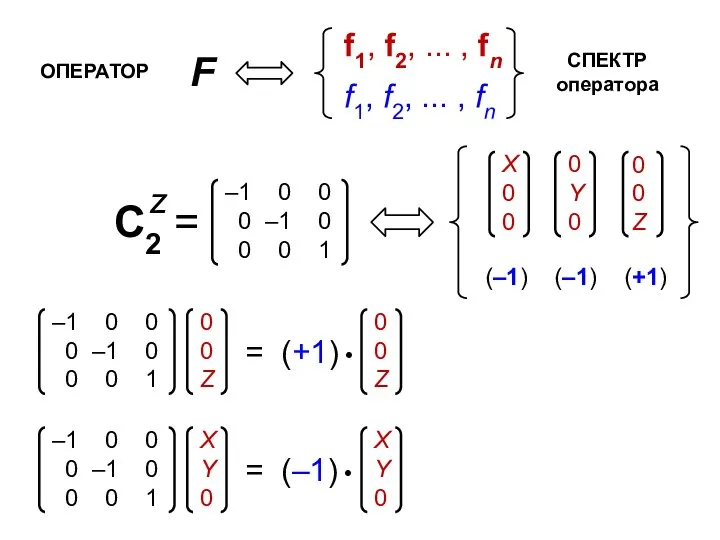
- 20. Спектральные свойства операторов Каждый оператор F имеет: набор СОБСТВЕННЫХ ВЕКТОРОВ (функций) ( f1, f2, ... ,
- 21. ОПЕРАТОР СПЕКТР оператора
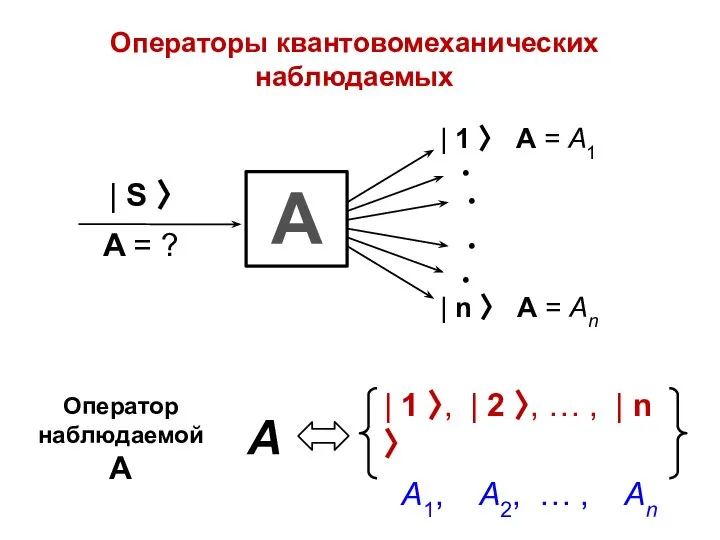
- 22. Операторы квантовомеханических наблюдаемых Оператор наблюдаемой А
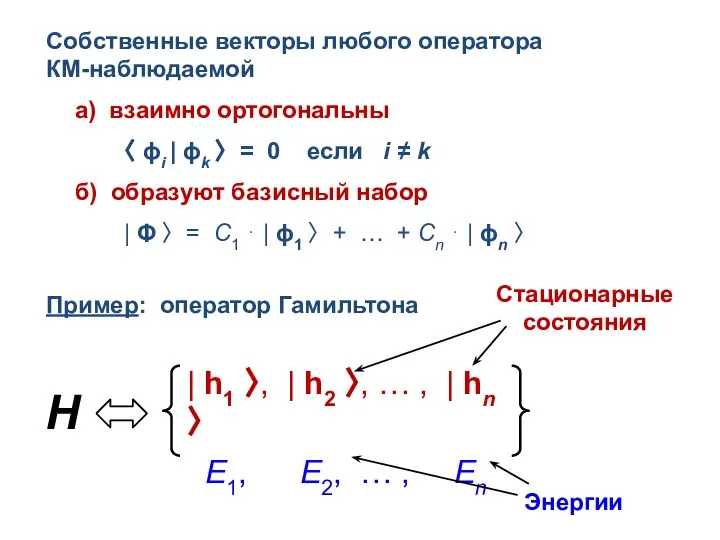
- 23. Собственные векторы любого оператора КМ-наблюдаемой а) взаимно ортогональны 〈 ϕi | ϕk 〉 = 0 если
- 24. Квантовые переходы в атоме 〈 2s | 1s 〉 = A1s→2s = 0 (векторы 1s и
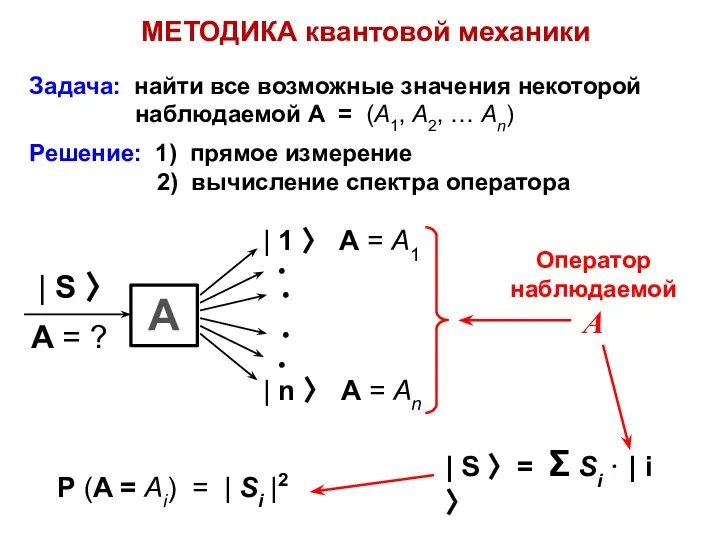
- 25. МЕТОДИКА квантовой механики Задача: найти все возможные значения некоторой наблюдаемой А = (А1, А2, … Аn)
- 26. Выводы 1. Всякой механической наблюдаемой А можно сопоставить оператор А 2. Оператор А является математической моделью
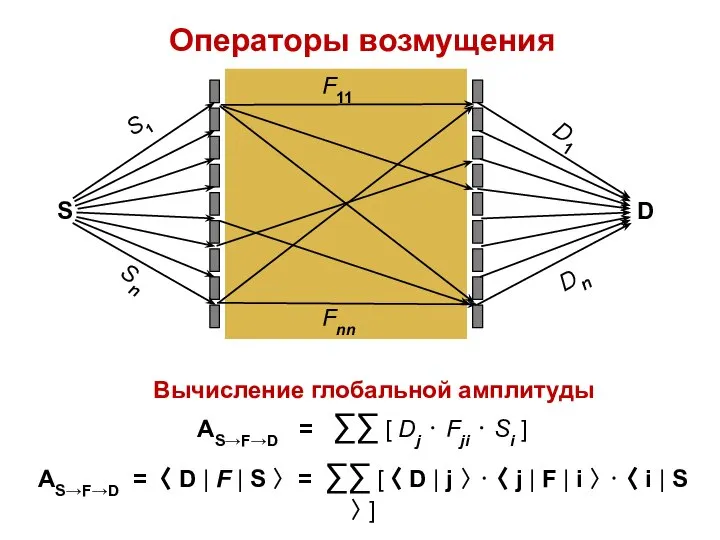
- 27. Операторы возмущения Вычисление глобальной амплитуды АS→F→D = ∑∑ [ Dj ⋅ Fji ⋅ Si ] АS→F→D
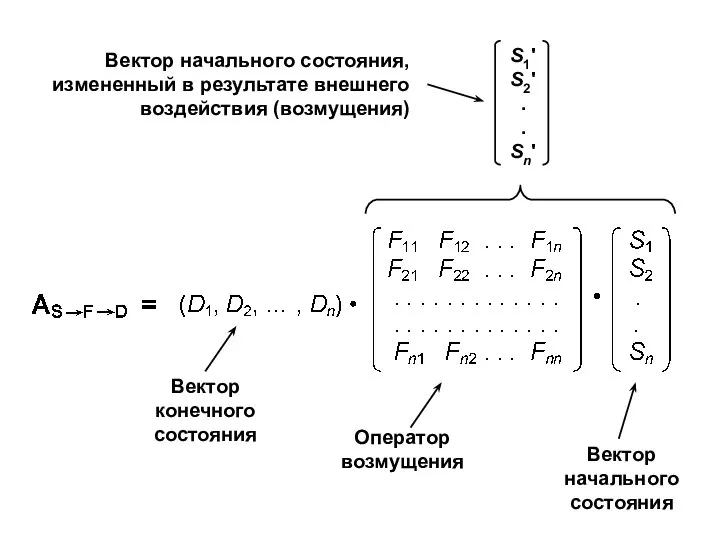
- 28. Вектор начального состояния, измененный в результате внешнего воздействия (возмущения)
- 29. Вывод В квантовой механике используют три разновидности операторов 1. Операторы наблюдаемых Применение а) вычисление допустимых значений
- 31. Скачать презентацию













 Droga krzyżowa
Droga krzyżowa Сравнительный анализ фазы отталкивания в различных способах прыжка в высоту с разбега у женщин
Сравнительный анализ фазы отталкивания в различных способах прыжка в высоту с разбега у женщин Производство суспензий и эмульсий
Производство суспензий и эмульсий Понятие, цели и этапы деловой оценки персонала
Понятие, цели и этапы деловой оценки персонала Рынок и отрасль
Рынок и отрасль  Методы расчета статически определимых систем на постоянную нагрузку
Методы расчета статически определимых систем на постоянную нагрузку Гипергенные процессы
Гипергенные процессы Личные права супругов по состоянию на данный момент
Личные права супругов по состоянию на данный момент Международное публичное право. ООН: история, структура, цели и задачи
Международное публичное право. ООН: история, структура, цели и задачи Автономный инвертор напряжения с синусоидальным выходным напряжением
Автономный инвертор напряжения с синусоидальным выходным напряжением Запорожье. Бердянск вчера и сегодня. - презентация
Запорожье. Бердянск вчера и сегодня. - презентация Поймай рыбку - презентация для начальной школы
Поймай рыбку - презентация для начальной школы ПОЛОЖИТЕЛЬНЫЙ СТОЛБ ТЛЕЮЩЕГО РАЗРЯДА
ПОЛОЖИТЕЛЬНЫЙ СТОЛБ ТЛЕЮЩЕГО РАЗРЯДА  Простейшие конструкции языка Pascal
Простейшие конструкции языка Pascal Белаз 7519
Белаз 7519 Программирование на языке С++
Программирование на языке С++ Шаблон_ПРЕДПРИЯТИЯ
Шаблон_ПРЕДПРИЯТИЯ Кроссфит
Кроссфит Конденсаторы и катушки индуктивности
Конденсаторы и катушки индуктивности Короли госзаказа
Короли госзаказа Реализация проекта «Аэродинамический комплекс»
Реализация проекта «Аэродинамический комплекс» «Виды и методы контроля знаний учащихся при изучении истории и обществознания»
«Виды и методы контроля знаний учащихся при изучении истории и обществознания» Разветвляющиеся алгоритмы
Разветвляющиеся алгоритмы 7 класс
7 класс  Wyrusz z Chrystusem na drogę krzyżową
Wyrusz z Chrystusem na drogę krzyżową СПИД
СПИД  Общие положения исполнения наказания
Общие положения исполнения наказания  Отношения Украины и России
Отношения Украины и России