Содержание
- 2. Решение задачи определения напряженно-деформированного состояния (НДС) сооружения состоит из следующих частей: − определение напряжений; − определение
- 3. 1. Определение опорных реакций Сооружение, воспринимая внешнюю нагрузку, через свои элементы передает ее опорам, а в
- 4. В элементах плоской стержневой системы возникают три внутренних усилия: 2. Внутренние усилия стержневой системы N −
- 5. Между Q и М существует дифференциальная зависимость (формула Журавского): Для определения знака Q по M ось
- 6. 3. Методы определения внутренних усилий Внутренние усилия определяются методами простых сечений, совместных сечений, вырезания узла и
- 7. 3.2. Метод совместных сечений Используется при расчете многодисковых систем. Например, при расчете трехдисковой рамы проводятся три
- 8. 3.3. Метод вырезания узла Используется для определения усилий простых систем. Его сущность: вырезается узел с не
- 9. 3.4. Метод замены связей Используется при расчете сложных статически определимых систем, которые трудно рассчитать другими способами.
- 10. Предыдущее уравнение примет вид: X + MC,P =0, где =1⋅ a = a – момент в
- 12. Скачать презентацию
Решение задачи определения напряженно-деформированного состояния (НДС) сооружения состоит из следующих
Решение задачи определения напряженно-деформированного состояния (НДС) сооружения состоит из следующих
− определение напряжений;
− определение опорных реакций и внутренних усилий;
− определение перемещений и деформаций.
При этом должны быть известны геометрические размеры и формы элементов сооружения, физические характеристики материала, внешняя нагрузка и особенности ее воздействия.
Расчет статически определимых систем является самой простой задачей, решаемой в строительной механике.
Статически определимой системой (СОС) называется система, внутренние усилия которой можно определять только из уравнений статики.
Особенности СОС:
− их внутренние усилия не зависят от упругих характеристик материала, форм сечений и площадей элементов;
− воздействие температуры, осадки опор, неточность изготовления элементов не вызывают внутренних усилий;
− если нет внешних нагрузок, все внутренние усилия равны нулю.
1. Определение опорных реакций
Сооружение, воспринимая внешнюю нагрузку, через свои
1. Определение опорных реакций
Сооружение, воспринимая внешнюю нагрузку, через свои
При определении опорных реакций используется принцип освобождения от связей: всякое тело можно освободить от связей, заменив их реакциями.
После этого из уравнений равновесия можно определять величины опорных реакций.
Уравнения равновесия плоской системы пишутся в трех формах:
1) ΣX = 0, ΣY = 0, ΣMA = 0
(ΣX и ΣY – суммы проекций сил на взаимно-пересекающиеся оси x и y, ΣMA – сумма моментов всех сил относительно любой точка A);
2) ΣX = 0, ΣMA = 0, ΣMB = 0
(точки A и B не должны лежать на одном перпендикуляре к оси x);
3) ΣMA = 0, ΣMB = 0, ΣMC = 0
(точки А, В, С не должны лежать на одной прямой).
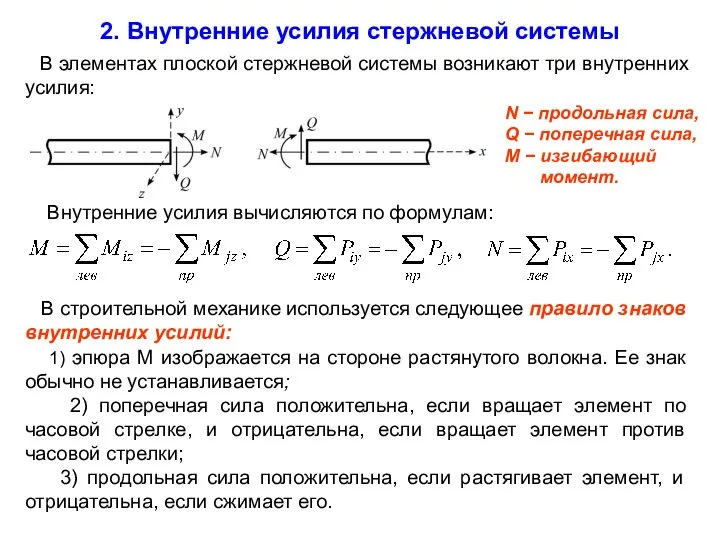
В элементах плоской стержневой системы возникают три внутренних усилия:
2. Внутренние
В элементах плоской стержневой системы возникают три внутренних усилия:
2. Внутренние
N − продольная сила,
Q − поперечная сила,
M − изгибающий
момент.
1) эпюра M изображается на стороне растянутого волокна. Ее знак обычно не устанавливается;
2) поперечная сила положительна, если вращает элемент по часовой стрелке, и отрицательна, если вращает элемент против часовой стрелки;
3) продольная сила положительна, если растягивает элемент, и отрицательна, если сжимает его.
В строительной механике используется следующее правило знаков внутренних усилий:
Внутренние усилия вычисляются по формулам:
Между Q и М существует дифференциальная зависимость (формула Журавского):
Для определения
Между Q и М существует дифференциальная зависимость (формула Журавского):
Для определения
Эпюры поперечных сил Q и продольных сил N можно изображать на любой стороне от оси стержня со своими знаком.
Но эпюру изгибающего момента M нужно обязательно изображать на стороне растянутого волокна.
3. Методы определения внутренних усилий
Внутренние усилия определяются методами
3. Методы определения внутренних усилий
Внутренние усилия определяются методами
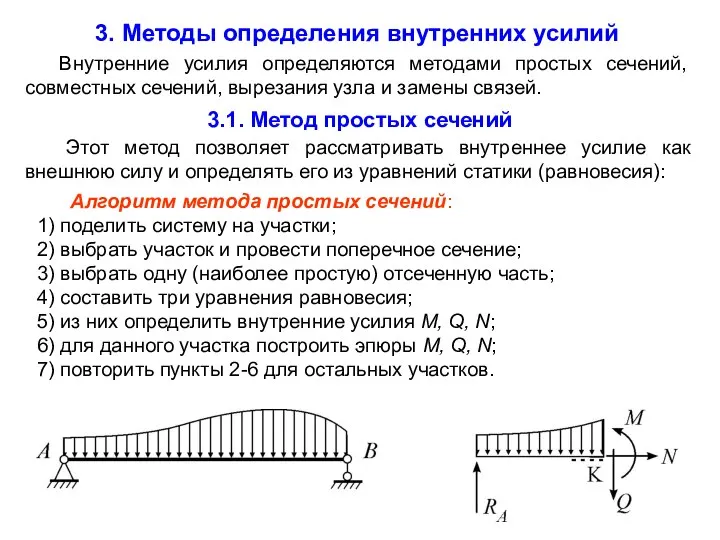
3.1. Метод простых сечений
Этот метод позволяет рассматривать внутреннее усилие как внешнюю силу и определять его из уравнений статики (равновесия):
Алгоритм метода простых сечений:
1) поделить систему на участки;
2) выбрать участок и провести поперечное сечение;
3) выбрать одну (наиболее простую) отсеченную часть;
4) составить три уравнения равновесия;
5) из них определить внутренние усилия M, Q, N;
6) для данного участка построить эпюры M, Q, N;
7) повторить пункты 2-6 для остальных участков.
3.2. Метод совместных сечений
Используется при расчете многодисковых систем.
Например,
3.2. Метод совместных сечений
Используется при расчете многодисковых систем.
Например,
Алгоритм метода совместных сечений:
1) совместными сечениями разделить систему на части (диски);
2) обозначить опорные и междисковые реакции;
3) для каждого диска записать уравнения равновесия;
4) решить систему полученных уравнений и определить реакции;
5) каждый диск рассчитать отдельно и построить эпюры;
6) объединить все эпюры в общие эпюры M, Q, N.
3.3. Метод вырезания узла
Используется для определения усилий простых систем.
3.3. Метод вырезания узла
Используется для определения усилий простых систем.
Рассмотрим пример:
После определения опорных реакций вырезается узел А и составляются уравнения равновесия:
ΣX = N2 cos45– N1 cos45= 0,
ΣY = N1sin45+ N2sin45+ P/2 = 0.
Из них определяются искомые продольные силы:
3.4. Метод замены связей
Используется при расчете сложных статически определимых систем,
3.4. Метод замены связей
Используется при расчете сложных статически определимых систем,
Его сущность: сложная система превращается в более простую путем перестановки одной связи в другое место; из условия эквивалентности заданной и заменяющей систем определяется усилие в переставленной связи; затем система рассчитывается известными способами.
Например, для расчета следующей рамы в заданной системе ЗС удалим правый вертикальный стержень и введем связь в левый шарнир. Тогда вместо шарнира получим припайку С, а стержни будут жестко связаны. Обозначив усилие в удаленной связи через X, получим основную систему ОС :
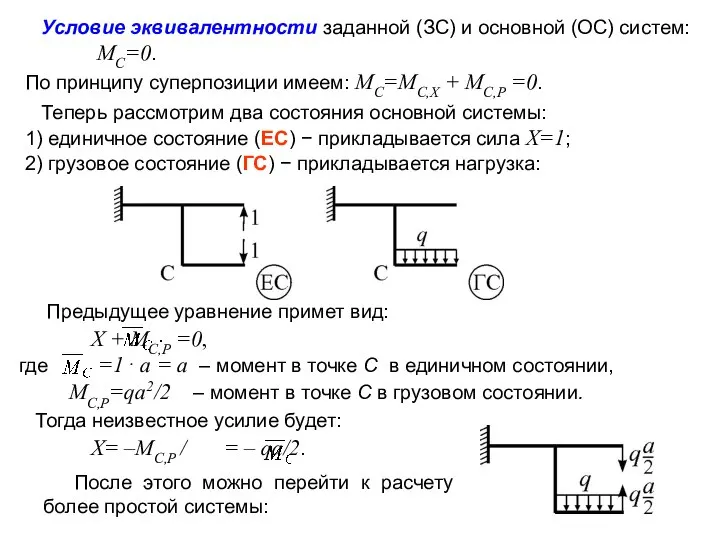
Предыдущее уравнение примет вид:
X + MC,P =0,
где =1⋅ a
Предыдущее уравнение примет вид:
X + MC,P =0,
где =1⋅ a
MC,P=qa2/2 – момент в точке С в грузовом состоянии.
Тогда неизвестное усилие будет:
X= –MC,P / = – qa/2.
Условие эквивалентности заданной (ЗС) и основной (ОС) систем:
MC=0.
По принципу суперпозиции имеем: MC=MC,X + MC,P =0.
Теперь рассмотрим два состояния основной системы:
1) единичное состояние (ЕС) − прикладывается сила X=1;
2) грузовое состояние (ГС) − прикладывается нагрузка:
После этого можно перейти к расчету более простой системы:






 Тема лекции: Противодиабетические средства Доцент кафедры общей и клинической фармакологии с курсом ФПК и ПК Владимир Михайл
Тема лекции: Противодиабетические средства Доцент кафедры общей и клинической фармакологии с курсом ФПК и ПК Владимир Михайл Сохранение природы. Вторичное использование вещей
Сохранение природы. Вторичное использование вещей Общая физическая и спортивная подготовка в системе физического воспитания. (Часть 2)
Общая физическая и спортивная подготовка в системе физического воспитания. (Часть 2) Презентация "Крымская Ярмарка" - скачать презентации по Экономике
Презентация "Крымская Ярмарка" - скачать презентации по Экономике Опорно-двигательная система человека Гейс Евгений 11 А
Опорно-двигательная система человека Гейс Евгений 11 А  Budowa i integracja systemów informacyjnych
Budowa i integracja systemów informacyjnych Портфель и архитектура бренда
Портфель и архитектура бренда Массивно-параллельные системы
Массивно-параллельные системы Сварочный выпрямитель
Сварочный выпрямитель Чрезвычайные ситуации на морском транспорте
Чрезвычайные ситуации на морском транспорте Начальная максимальная цена контракта
Начальная максимальная цена контракта Литература и искусство первой половины XIX века
Литература и искусство первой половины XIX века Роль физической активности и спорта в сохранении здоровья
Роль физической активности и спорта в сохранении здоровья Бюджетний процес у Франції
Бюджетний процес у Франції Сборник материалов о зайце Составила Бутакова Валерия, ученица 2 класса
Сборник материалов о зайце Составила Бутакова Валерия, ученица 2 класса Методическое пособие для школьных психологов «Психологическая подготовка учащихся к ЕГЭ»
Методическое пособие для школьных психологов «Психологическая подготовка учащихся к ЕГЭ» Вспомогательный алгоритм
Вспомогательный алгоритм Систематизация и классификация знаний в судебной экспертизе
Систематизация и классификация знаний в судебной экспертизе Принятие ислама башкирами
Принятие ислама башкирами Презентация "Экономика и ее роль в жизни общества" - скачать презентации по Экономике_
Презентация "Экономика и ее роль в жизни общества" - скачать презентации по Экономике_ Недействительность сделки, совершенной под влиянием заблуждения Подготовила: студентка ФТД-2, группы Т094 Алиев Эльвин
Недействительность сделки, совершенной под влиянием заблуждения Подготовила: студентка ФТД-2, группы Т094 Алиев Эльвин Презентация Полимеры и пластмассы
Презентация Полимеры и пластмассы Участие в системе БЭСП Банка России: требования, порядок и управление участием
Участие в системе БЭСП Банка России: требования, порядок и управление участием Дидактическая игра «ОПРЕДЕЛИ музыкальный ИНСТРУМЕНТ» .
Дидактическая игра «ОПРЕДЕЛИ музыкальный ИНСТРУМЕНТ» .  Защита детей от информации, причиняющей вред их здоровью развитию
Защита детей от информации, причиняющей вред их здоровью развитию Свойства веществ
Свойства веществ  кто работает на свиной фабрике - презентация для начальной школы
кто работает на свиной фабрике - презентация для начальной школы Изобразительное искусство в семье пластических искусств
Изобразительное искусство в семье пластических искусств