Содержание
- 2. Здесь Δt - шаг дискретизации, который связан с частотой Найквиста F формулой. (2) На прошлой лекции
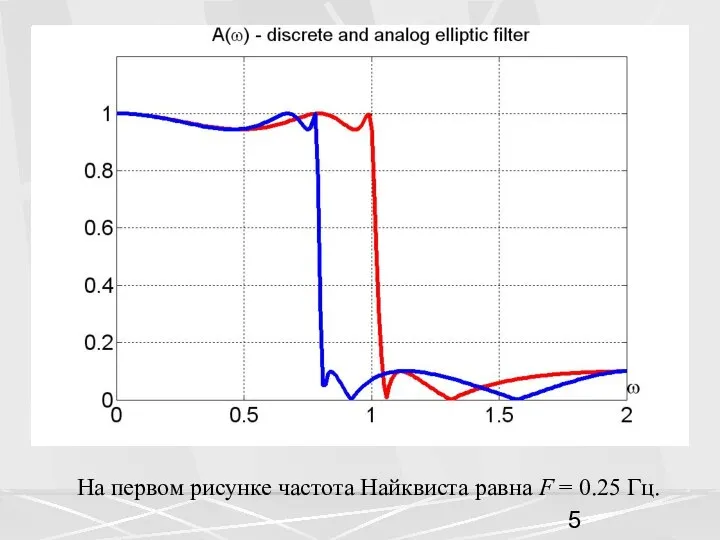
- 3. Значок « d » относится к дискретному фильтру, а значок « a » к аналоговому фильтру.
- 4. Поэтому можно говорить только о приближенном совпадении частотных характеристик дискретного и аналогового фильтров. Как отмечалось на
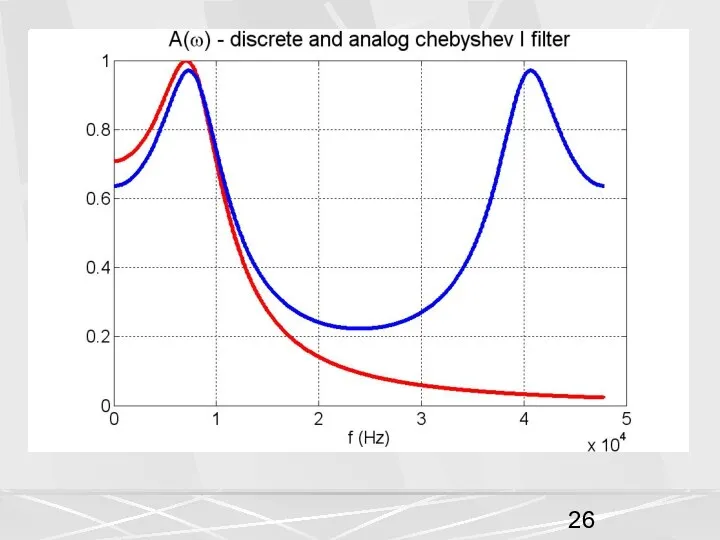
- 5. На первом рисунке частота Найквиста равна F = 0.25 Гц.
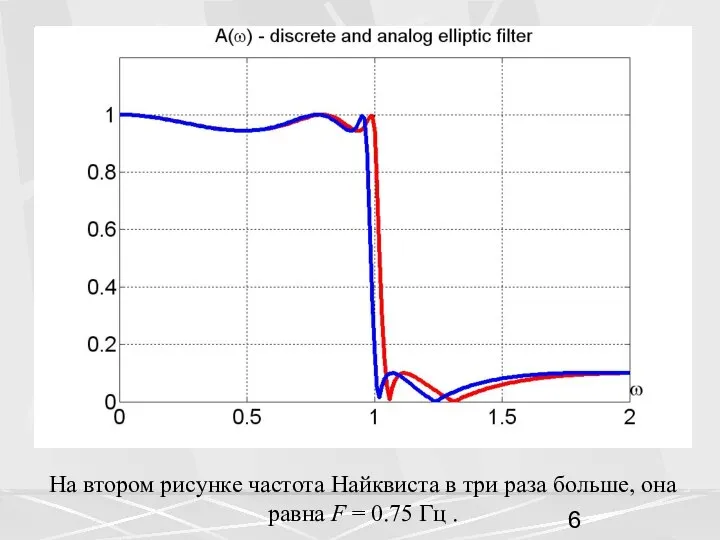
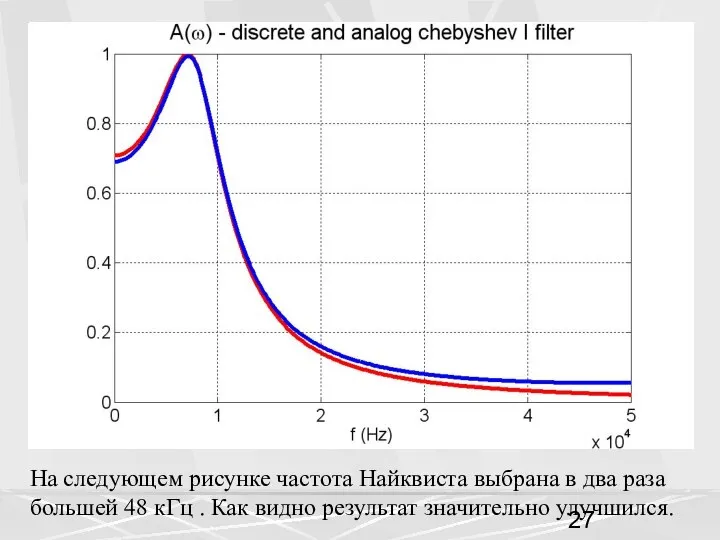
- 6. На втором рисунке частота Найквиста в три раза больше, она равна F = 0.75 Гц .
- 7. На первом рисунке отношение (6) для частоты среза ω0 = 1 рад/с равно. (7) Поэтому условие
- 8. Поэтому условие (6) в полосе пропускания выполняется лучше, отсюда неплохое совпадения АЧХ дискретного и аналогового фильтров
- 9. Однако, хорошее совпадение частотных характеристик дискретного и аналогового фильтров при малых частотах в полосе пропускания, не
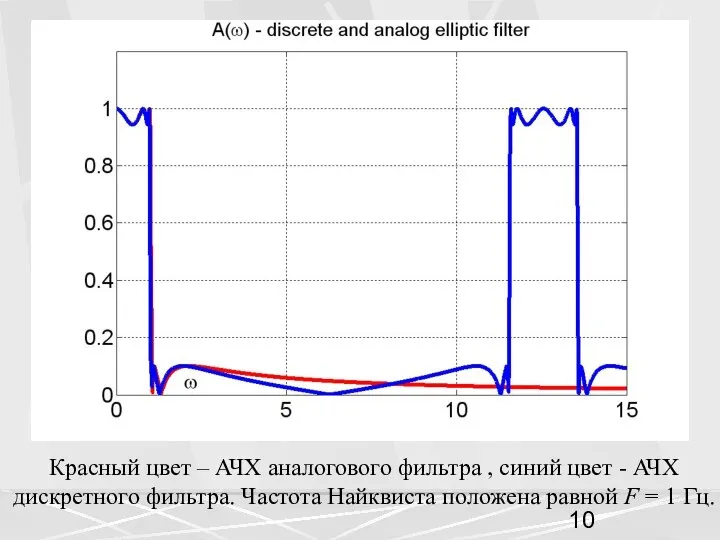
- 10. Красный цвет – АЧХ аналогового фильтра , синий цвет - АЧХ дискретного фильтра. Частота Найквиста положена
- 11. Геометрические свойства билинейного преобразования Как известно из теории функций комплексного переменного, билинейное преобразование (10) осуществляет конформное
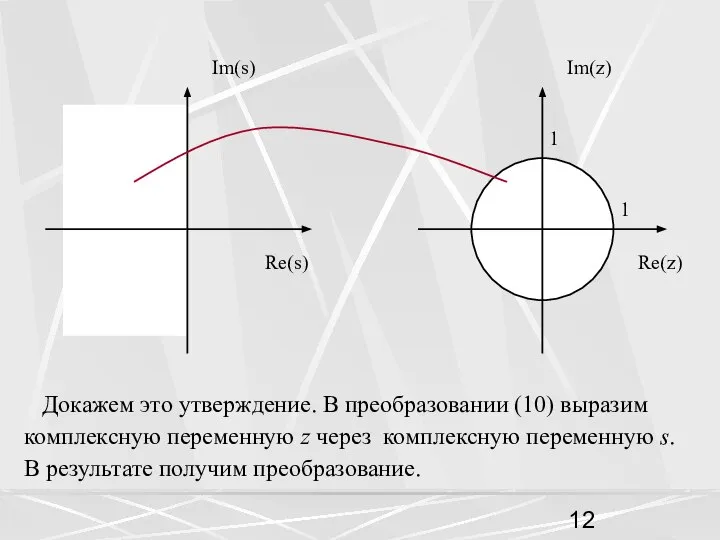
- 12. Докажем это утверждение. В преобразовании (10) выразим комплексную переменную z через комплексную переменную s. В результате
- 13. (11) Найдем квадрат модуля комплексного числа z . (12) Обозначим u, v, действительную и мнимую части
- 14. Для любой точки в левой полуплоскости комплексной s- плоскости действительная часть – это отрицательное число. Обозначим
- 15. В дроби (16) числитель меньше знаменателя, поэтому дробь (16) меньше единицы. Отсюда получаем условие. (17) Таким
- 16. Другими словами, точки мнимой оси комплексной s- плоскости, с помощью билинейного преобразования отображаются в точки лежащие
- 17. Далее вспоминаем, что условием устойчивости дискретного фильтра. Дискретный фильтр является устойчивым фильтром, если все полюсы его
- 18. Метод инвариантной импульсной характеристики Метод инвариантной импульсной характеристики (impulse invariance) синтезирует рекурсивный фильтр с помощью дискретизации
- 19. Схему синтеза дискретного фильтра можно представить в следующем виде. (19) По известной передаточной функции Ha (s)
- 20. На самом деле, чтобы получить частотную характеристику Kd (ω) дискретного фильтра по аналоговому прототипу с помощью
- 21. Здесь S(f) – спектр непрерывного сигнала, SD( f ) - спектр дискретного сигнала, F - частота
- 22. Вспомним из прошлой лекции, как выражаются частотные характеристики аналогового и дискретного фильтров через свои частотные характеристики.
- 23. Если импульсную характеристику аналогового фильтра рассматривать как непрерывный сигнал, а импульсную характеристику дискретного фильтра рассматривать как
- 24. Частотные характеристики аналоговых фильтров, которые мы рассмотрели выше, были нормированы на единицу. Дальше мы это тоже
- 25. Формулы (25), (26) являются основными в методе инвариантной импульсной характеристики . В качестве примера синтезируем методом
- 27. На следующем рисунке частота Найквиста выбрана в два раза большей 48 кГц . Как видно результат
- 28. Синтез нерекурсивных фильтров с использованием окон Нерекурсивные фильтры – это фильтры без обратной связи. Нерекурсивные фильтры
- 29. Поэтому передаточная функция нерекурсивного фильтра имеет следующий вид. (27) Вспомним, как выражается передаточная функция через импульсную
- 30. Кроме того, элементы импульсной характеристики h(n) совпадают с коэффициентами bn основного уравнения фильтра. (30) Число N
- 31. Таким образом, если мы имеем нерекурсивный фильтр порядка N, и нам известна импульсная характеристика h(n) ,
- 32. Увеличение порядка фильтра N означает увеличение электрических элементов в конструкции фильтра. Поэтому N является всегда конечным
- 33. Метод окон является одним их таких методов синтеза нерекурсивных фильтров. В основе этого метода лежит прямое
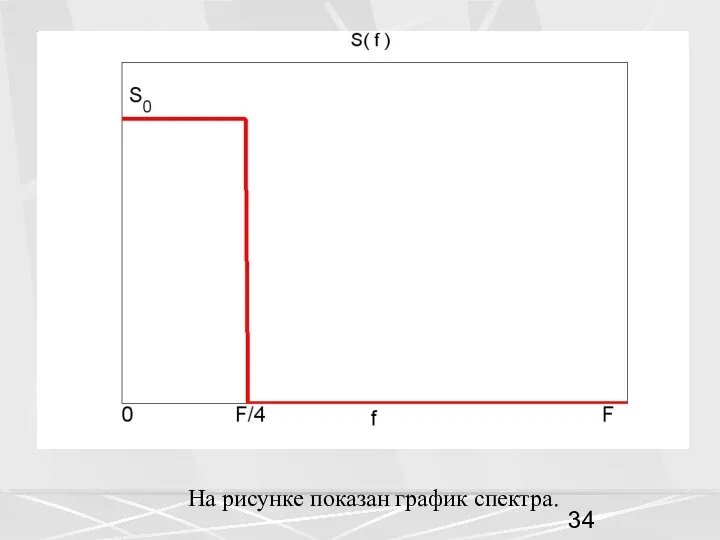
- 34. На рисунке показан график спектра.
- 35. Так как мы собираемся рассматривать действительные сигналы (импульсные характеристики), то спектр, как известно, должен быть четной
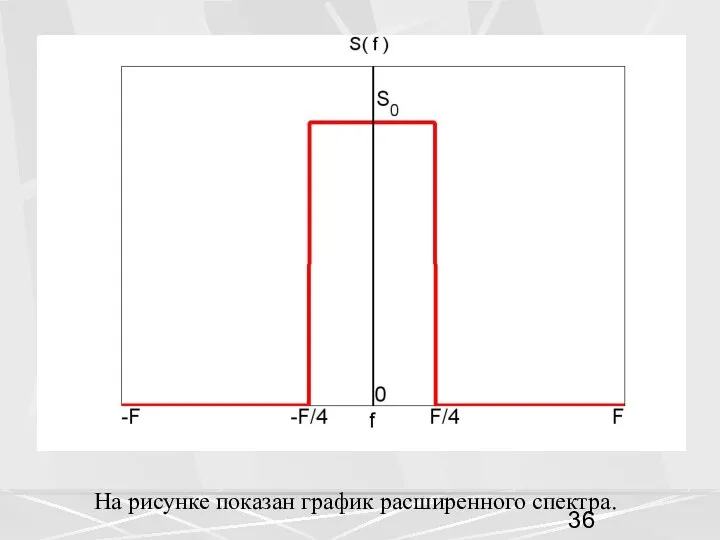
- 36. На рисунке показан график расширенного спектра.
- 37. Подставляем (35) в интеграл (32), интегрируем и получаем элементы дискретного сигнала (35) Полученный дискретный сигнал имеет
- 38. Для удобства мы положили множитель в (35) равным. Для построения графика дискретного сигнала (36) положим число
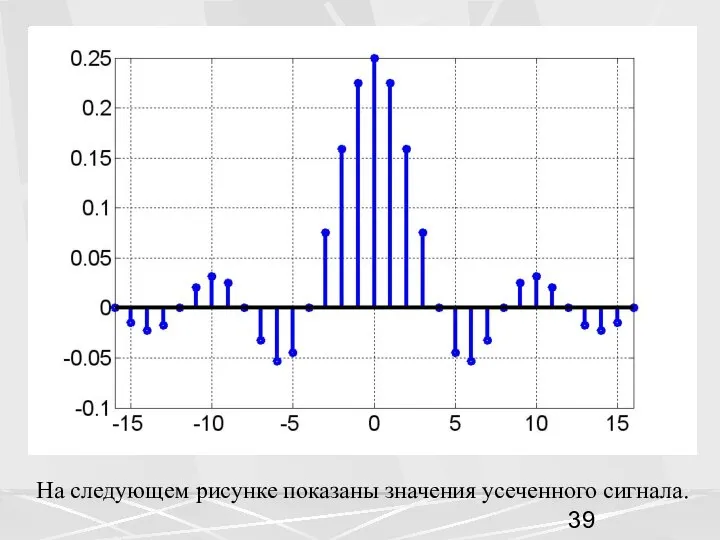
- 39. На следующем рисунке показаны значения усеченного сигнала.
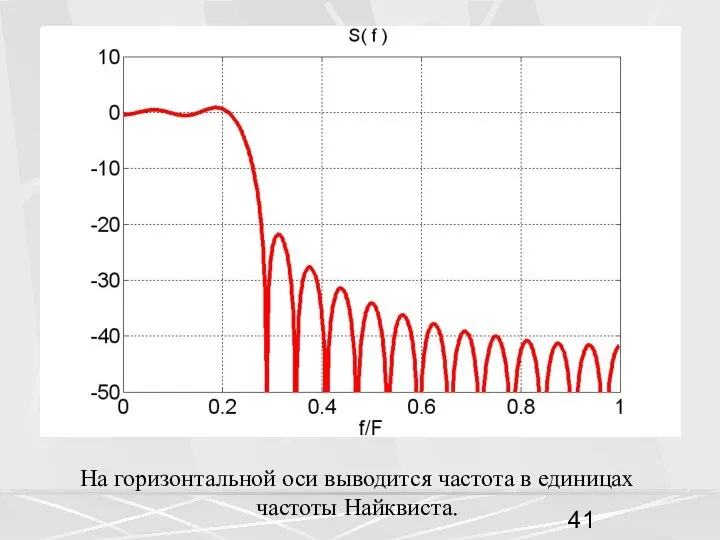
- 40. Этот усеченный дискретный сигнал подставляем в ряд Фурье (32), который теперь является конечной суммой. (38) Посмотрим,
- 41. На горизонтальной оси выводится частота в единицах частоты Найквиста.
- 42. Теперь нам надо связать дискретный сигнал с импульсной характеристикой фильтра, а спектр дискретного сигнала с частотной
- 43. Тогда частотная характеристика фильтра и спектр дискретного сигнала будут связаны соотношение. (40) Таким образом, переход от
- 44. Весовые функции, окна При переходе от дискретного сигнала к импульсной характеристики фильтра, мы бесконечную последовательность усекли
- 45. Весовая функция прямоугольного окна имеет вид. (42) В рассмотренном примере, мы полагали число M равным. Весовая
- 46. Это преобразование будем обозначать следующим символом. (44) У весовой функции имеется свой Фурье образ. (45) Перемножаем
- 47. Далее мы находим спектр нового сигнала по формулам (43). Как известно из теории преобразований Фурье, новый
- 48. Импульсная функция фильтра будет находится из нового ограниченного дискретного сигнала. (49) Весовых функций существует довольно много.
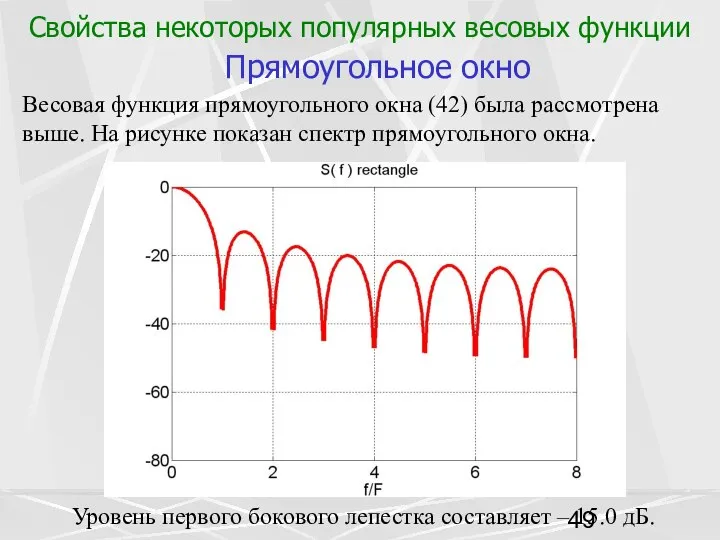
- 49. Свойства некоторых популярных весовых функции Прямоугольное окно Весовая функция прямоугольного окна (42) была рассмотрена выше. На
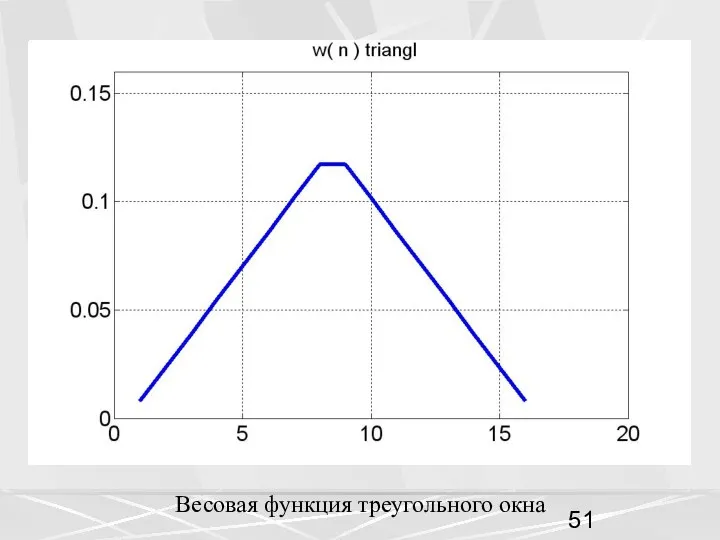
- 50. Треугольное окно Отсчеты треугольного окна рассчитываются по следующей формуле, для нечетный n. (50) Для четных n
- 51. Весовая функция треугольного окна
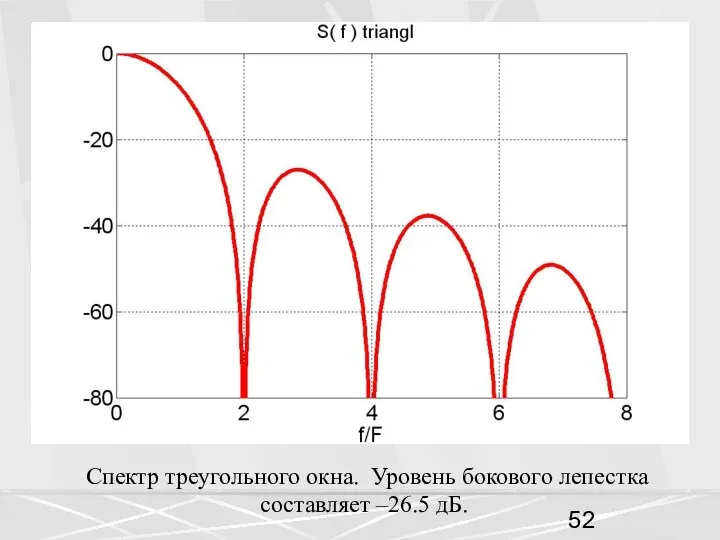
- 52. Спектр треугольного окна. Уровень бокового лепестка составляет –26.5 дБ.
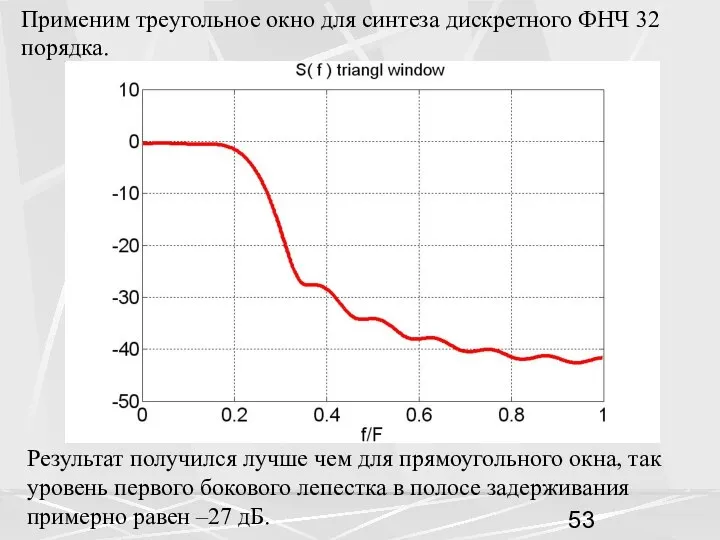
- 53. Результат получился лучше чем для прямоугольного окна, так уровень первого бокового лепестка в полосе задерживания примерно
- 54. Окно Бартлетта Окно Бартлетта, по сути дела, тоже является треугольным окном, но рассчитывается несколько иначе. Для
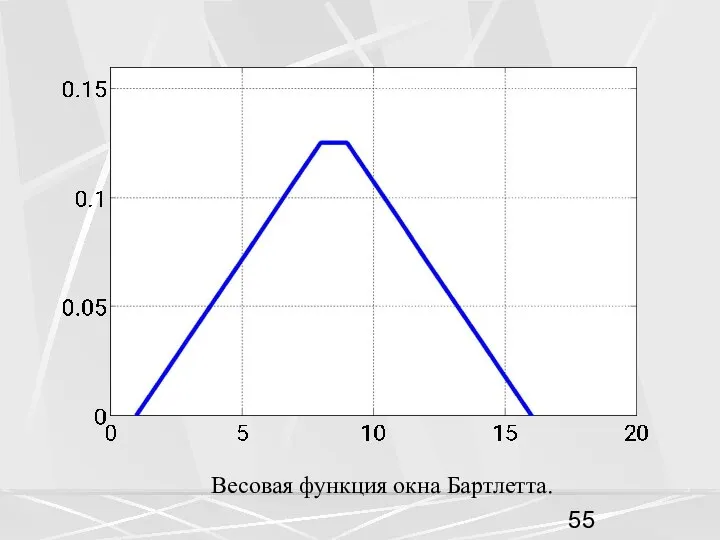
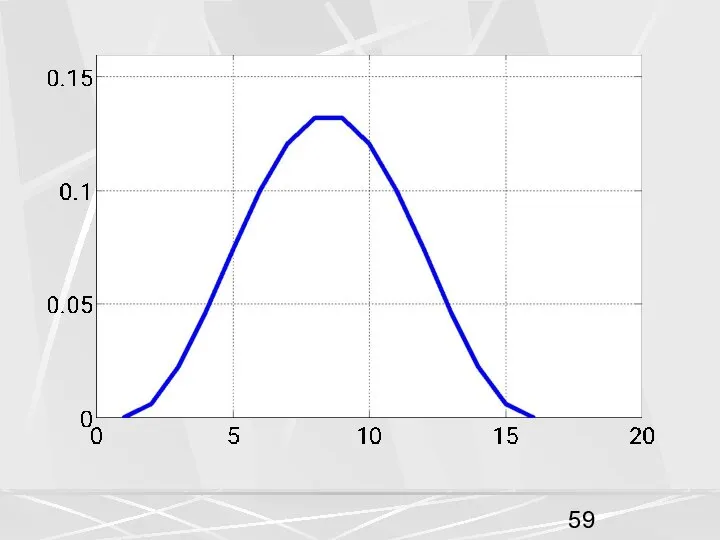
- 55. Весовая функция окна Бартлетта.
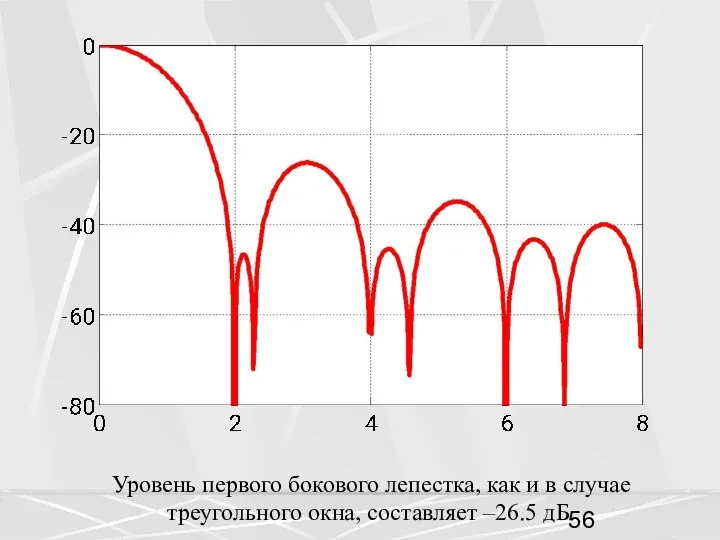
- 56. Уровень первого бокового лепестка, как и в случае треугольного окна, составляет –26.5 дБ.
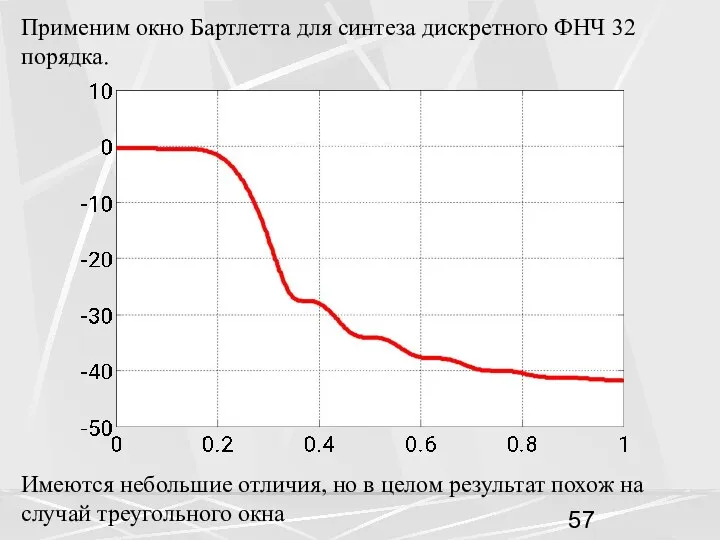
- 57. Имеются небольшие отличия, но в целом результат похож на случай треугольного окна Применим окно Бартлетта для
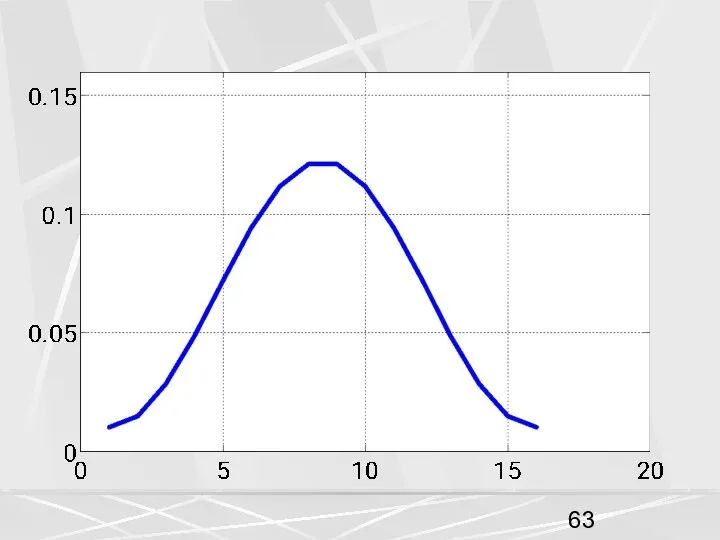
- 58. Окно Ханна Отсчеты окна Ханна рассчитываются по формуле: (54) На рисунках показаны весовая функция окна Ханна,
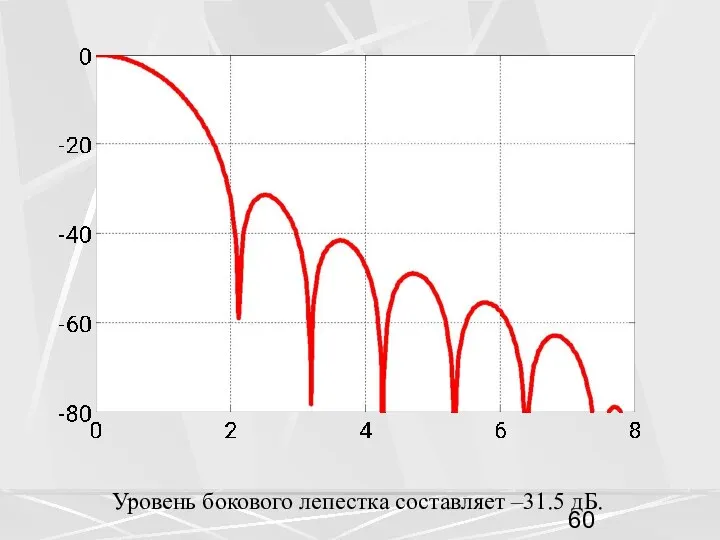
- 60. Уровень бокового лепестка составляет –31.5 дБ.
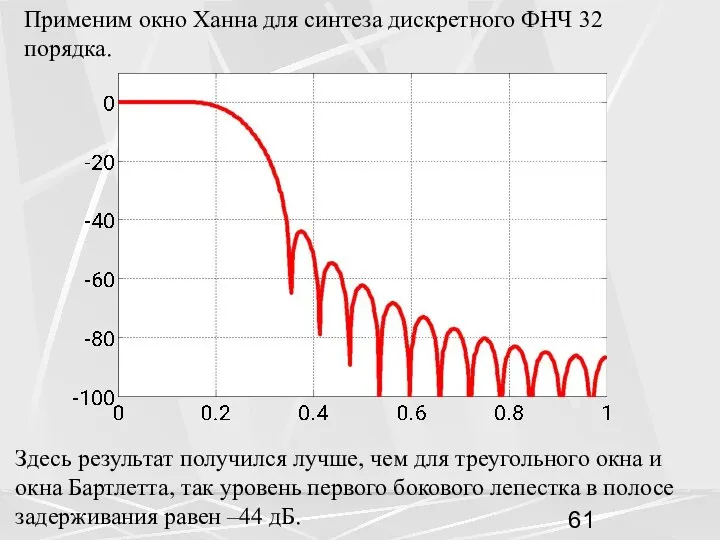
- 61. Применим окно Ханна для синтеза дискретного ФНЧ 32 порядка. Здесь результат получился лучше, чем для треугольного
- 62. Окно Хэмминга Отсчеты окна Хэмминга рассчитываются по формуле (55) На рисунках показаны весовая функция окна Хэмминга,
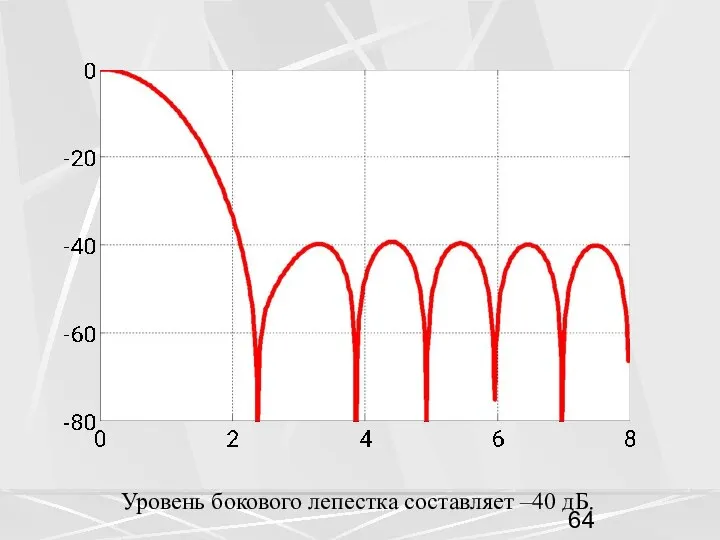
- 64. Уровень бокового лепестка составляет –40 дБ.
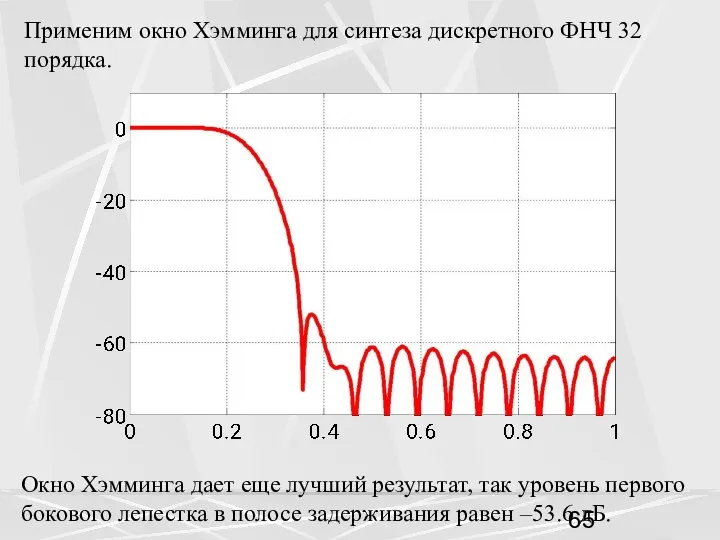
- 65. Применим окно Хэмминга для синтеза дискретного ФНЧ 32 порядка. Окно Хэмминга дает еще лучший результат, так
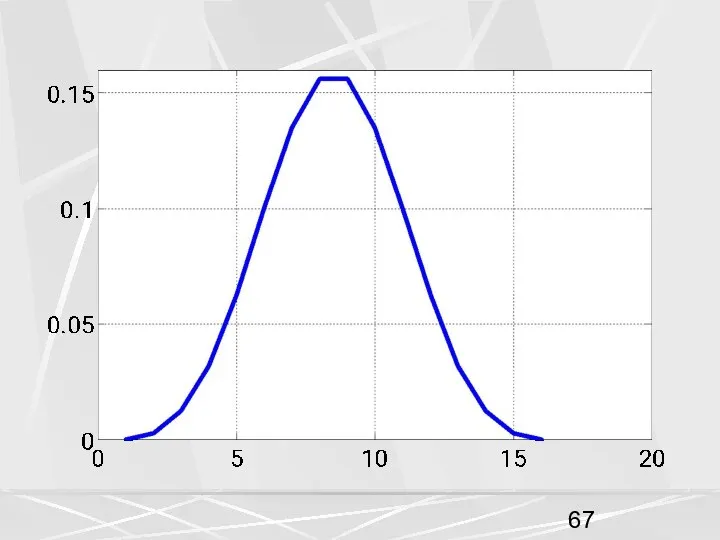
- 66. Окно Блэкмена Отсчеты окна Блэкмена рассчитываются по формуле . (55) На рисунках показаны весовая функция окна
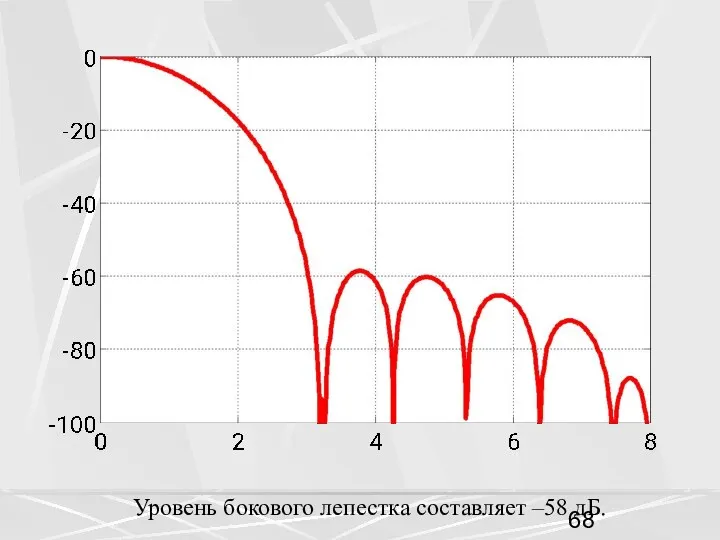
- 68. Уровень бокового лепестка составляет –58 дБ.
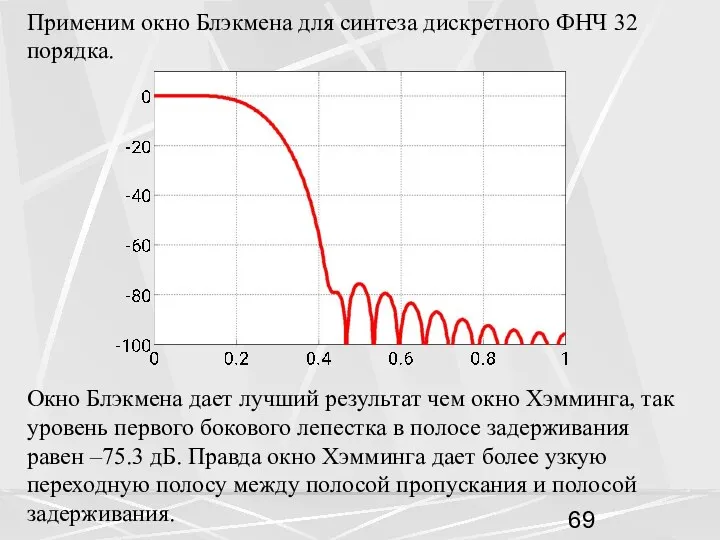
- 69. Применим окно Блэкмена для синтеза дискретного ФНЧ 32 порядка. Окно Блэкмена дает лучший результат чем окно
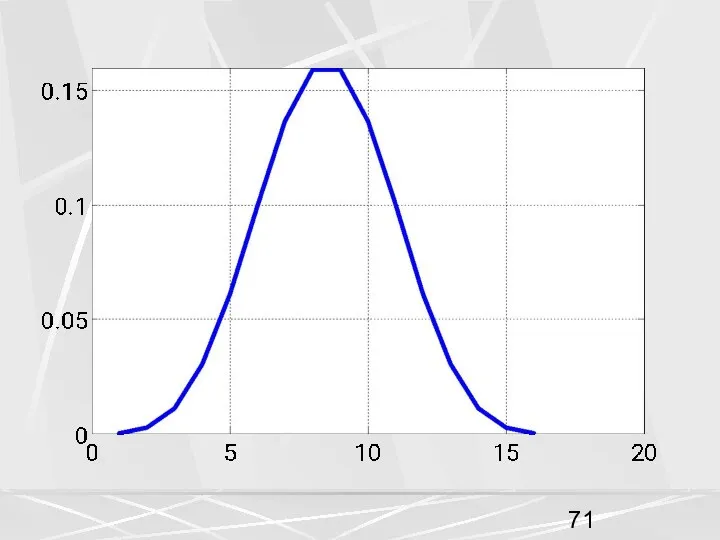
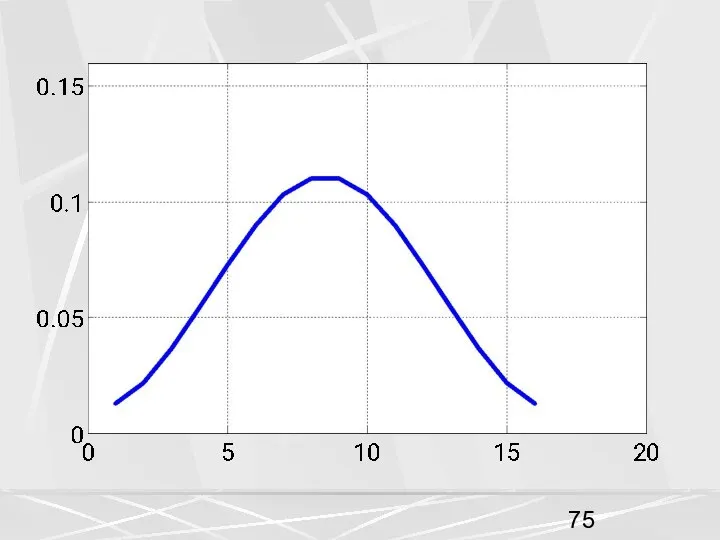
- 70. Окно Кайзера Отсчеты окна Кайзера рассчитываются по формуле : (56) Здесь I0 (z) - модифицированная функция
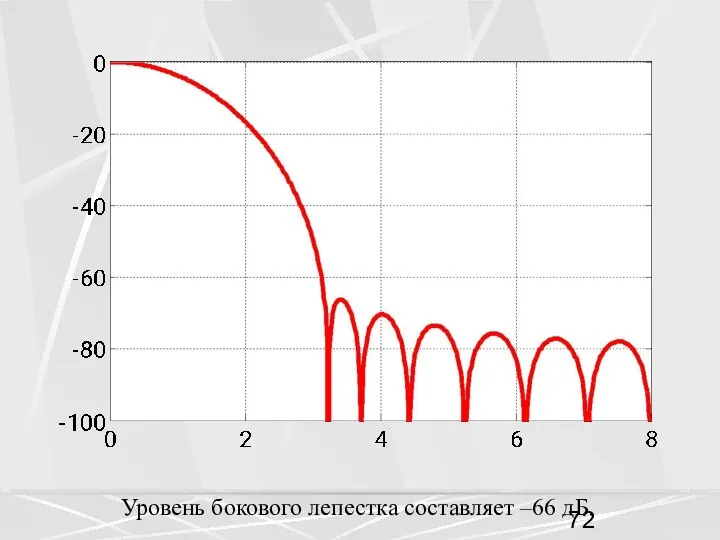
- 72. Уровень бокового лепестка составляет –66 дБ.
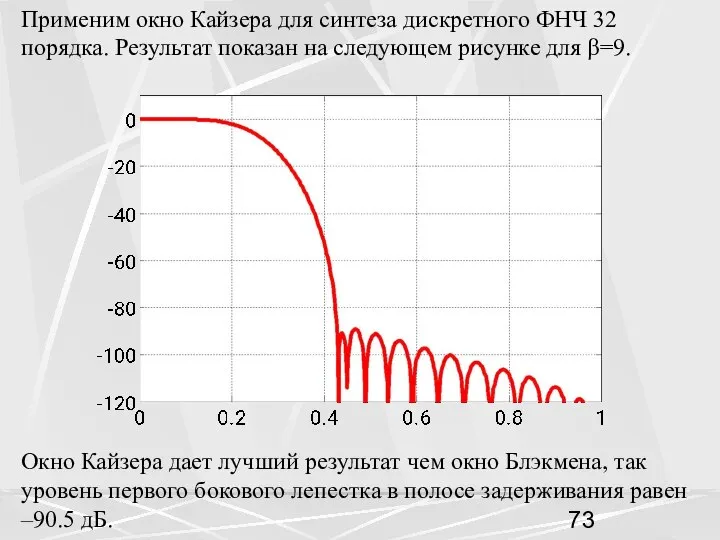
- 73. Применим окно Кайзера для синтеза дискретного ФНЧ 32 порядка. Результат показан на следующем рисунке для β=9.
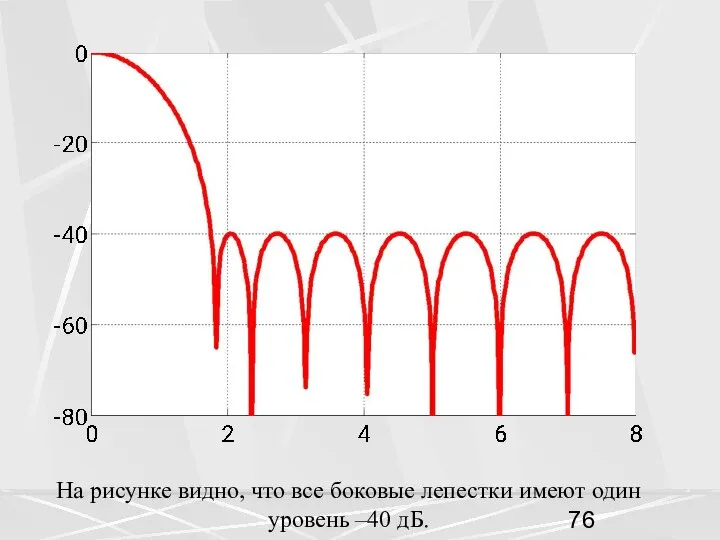
- 74. Окно Чебышева Для окна Чебышева все боковые лепестки имеют одинаковый уровень, заданный при расчете окна. Отчеты
- 76. На рисунке видно, что все боковые лепестки имеют один уровень –40 дБ.
- 78. Скачать презентацию












































 Художественные системы в проектировании одежды
Художественные системы в проектировании одежды Клетка живого организма
Клетка живого организма  СКАЗКИ ИРАССКАЗЫ Л.Н. ТОЛСТОГО Составила: Зименина О.С. учитель начальных классов МОУ «СОШ №7» им. Н.В. Кордюкова Г. Кимовск
СКАЗКИ ИРАССКАЗЫ Л.Н. ТОЛСТОГО Составила: Зименина О.С. учитель начальных классов МОУ «СОШ №7» им. Н.В. Кордюкова Г. Кимовск Троица – это Бог-Отец, Бог-Сын и Бог-Святой дух
Троица – это Бог-Отец, Бог-Сын и Бог-Святой дух Математическое кафе 7-8 класс
Математическое кафе 7-8 класс ROUTING-6
ROUTING-6  Компьютерная графика
Компьютерная графика  Основы социально-гигиенического мониторинга
Основы социально-гигиенического мониторинга  Презентация Системный подход
Презентация Системный подход Государственный строй: система институтов, их компетенция и механизм взаимодействия по Конституции 1871 года. Выполнили: студентки
Государственный строй: система институтов, их компетенция и механизм взаимодействия по Конституции 1871 года. Выполнили: студентки  Системы регулирования тепловой энергии. ЭкономиКомфорт и ЭкономиКомфорт-IP
Системы регулирования тепловой энергии. ЭкономиКомфорт и ЭкономиКомфорт-IP Рак прямой кишки
Рак прямой кишки Моим ученикам - презентация для начальной школы
Моим ученикам - презентация для начальной школы Минутка чистописания . Ш рока стр на м я р дная, Много в ней л сов, п лей и рек!
Минутка чистописания . Ш рока стр на м я р дная, Много в ней л сов, п лей и рек! Технический рисунок
Технический рисунок Диаграмма Исикавы. «Рыбий скелет Исикавы» Выполнила студентка ФТД-4 гурппы ДС-06 Лепичева Наталия
Диаграмма Исикавы. «Рыбий скелет Исикавы» Выполнила студентка ФТД-4 гурппы ДС-06 Лепичева Наталия Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Презентация универсальной спортивной площадки в парке отдыха п. Афанасьево
Презентация универсальной спортивной площадки в парке отдыха п. Афанасьево Опера – это… Опера возникла в ….веке, в …( страна) Русский композитор, первопроходец в жанре оперы: Его оперы:… Оперетта- это… Отличие оперы от оперетты… Русский советский композитор, работавший в жанре оперетты:…
Опера – это… Опера возникла в ….веке, в …( страна) Русский композитор, первопроходец в жанре оперы: Его оперы:… Оперетта- это… Отличие оперы от оперетты… Русский советский композитор, работавший в жанре оперетты:… Задание: реализовать класс валидации (Java)
Задание: реализовать класс валидации (Java) Презентация "Оценка эффективности" - скачать презентации по Экономике
Презентация "Оценка эффективности" - скачать презентации по Экономике Технология Fast Ethernet
Технология Fast Ethernet Моделирование расчетных сейсмических воздействий
Моделирование расчетных сейсмических воздействий Арабо-мусульманская цивилизация
Арабо-мусульманская цивилизация Культура античности. Эгейское искусство
Культура античности. Эгейское искусство Общая характеристика феодального государства и права.
Общая характеристика феодального государства и права. MTN.Win.01 Основы компьютерных сетей. Введение в сетевые технологии
MTN.Win.01 Основы компьютерных сетей. Введение в сетевые технологии Морские узлы
Морские узлы