Содержание
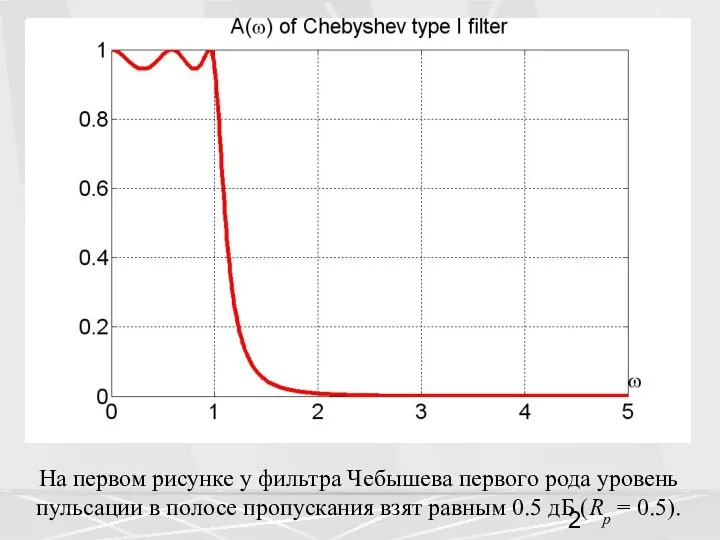
- 2. На первом рисунке у фильтра Чебышева первого рода уровень пульсации в полосе пропускания взят равным 0.5
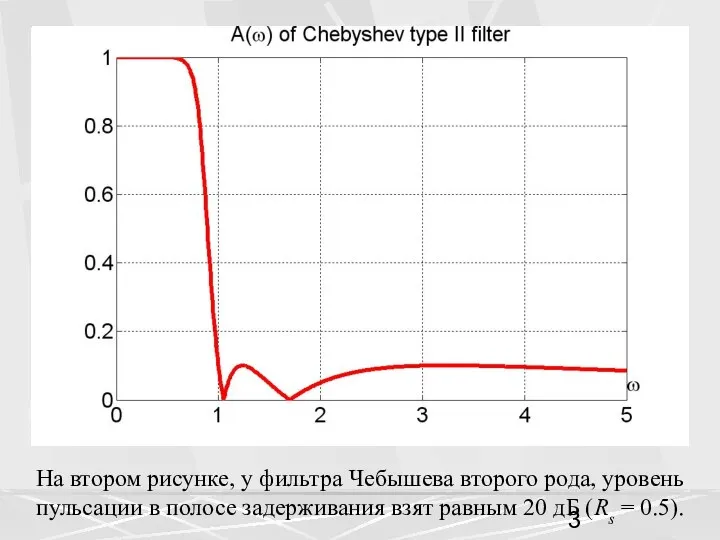
- 3. На втором рисунке, у фильтра Чебышева второго рода, уровень пульсации в полосе задерживания взят равным 20
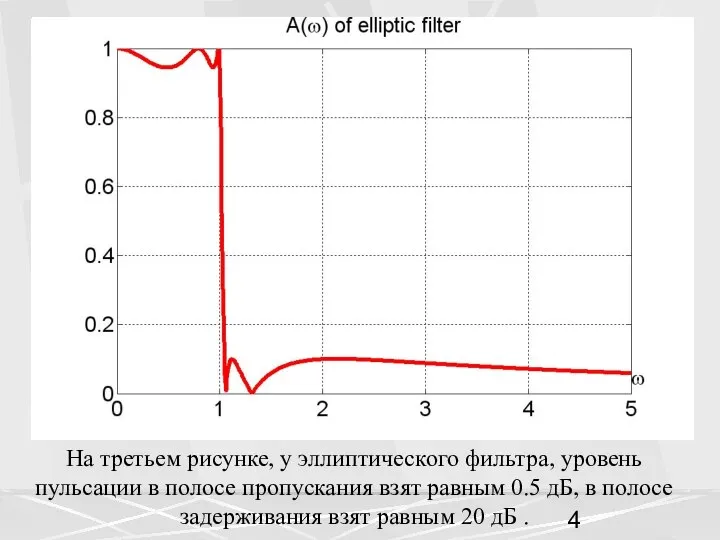
- 4. На третьем рисунке, у эллиптического фильтра, уровень пульсации в полосе пропускания взят равным 0.5 дБ, в
- 5. Эллиптический фильтр в советской и российской литературе называют также фильтром Золотарева – Кауэра. В английской литературе
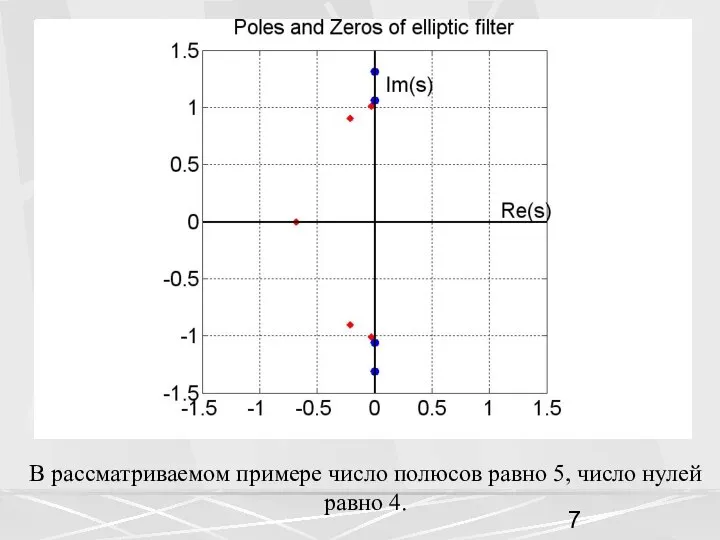
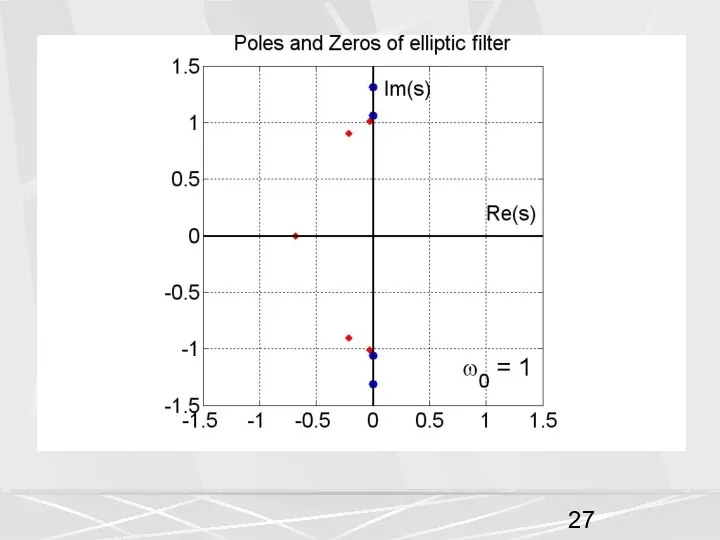
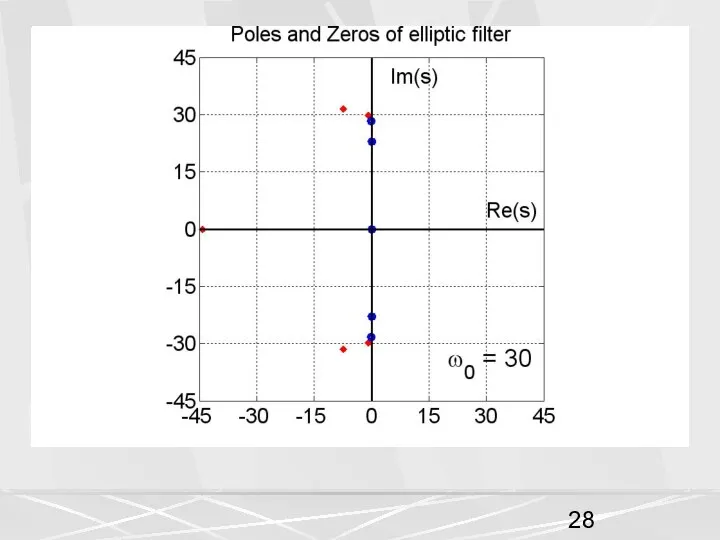
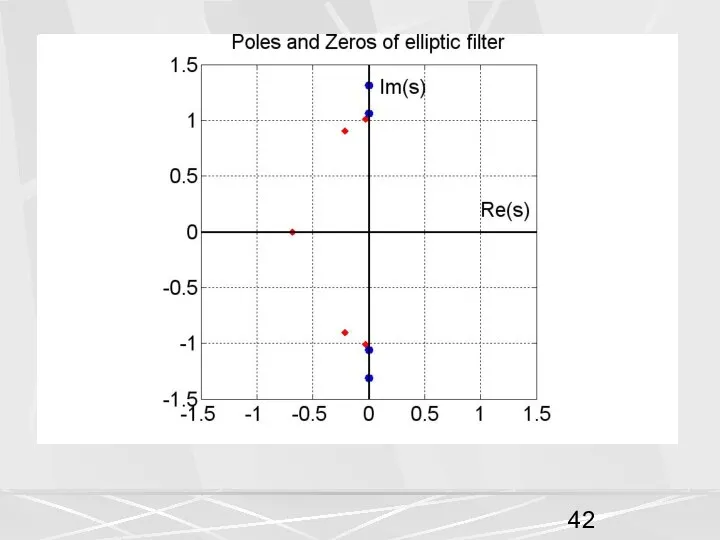
- 6. Эллиптический фильтр имеет как полюсы, так и нули. Число полюсов Np определяется порядком фильтра. Число нулей
- 7. В рассматриваемом примере число полюсов равно 5, число нулей равно 4.
- 8. АЧХ эллиптического фильтра, в общем случае описывается следующей аналитической формулой. (1) Здесь - ω0 частота среза,
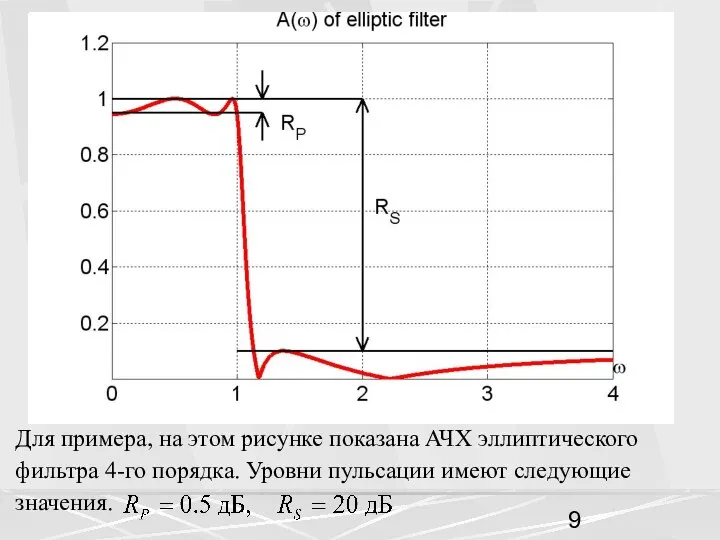
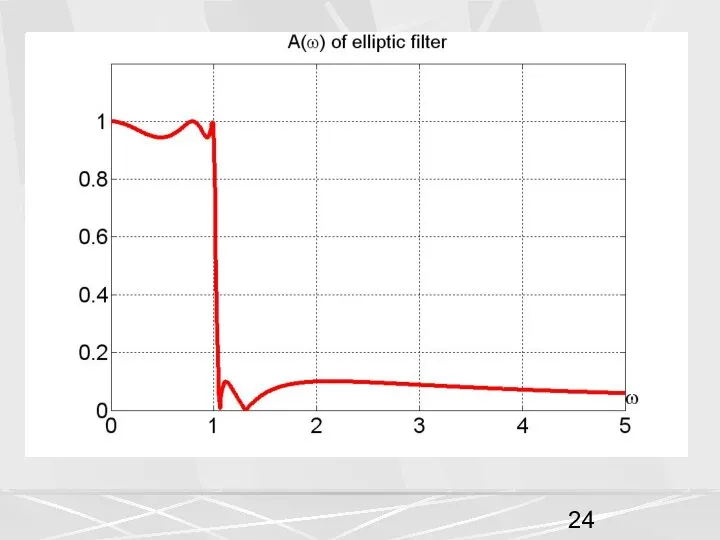
- 9. Для примера, на этом рисунке показана АЧХ эллиптического фильтра 4-го порядка. Уровни пульсации имеют следующие значения.
- 10. Уровни пульсации позволяют найти следующие характерные значения АЧХ. Наименьшее значение пульсаций Ap в полосе пропускания находится
- 11. Используя формулы (2), (3) для выбранных значений уровней пульсации получаем Действительно такие значения показаны на рисунке.
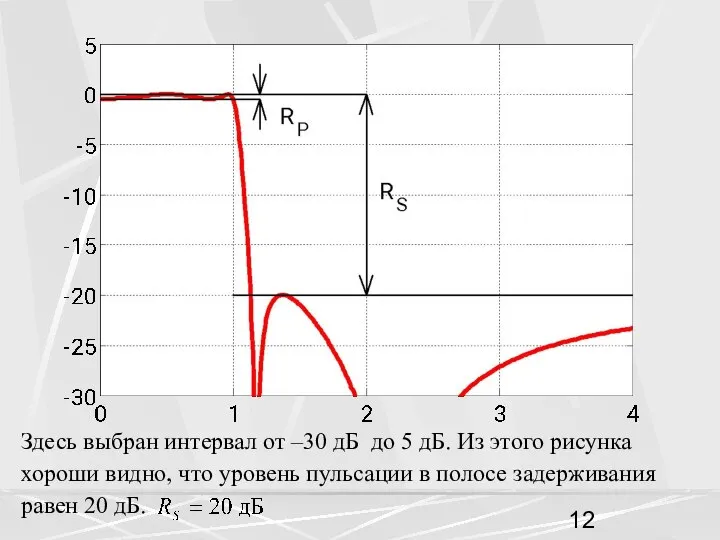
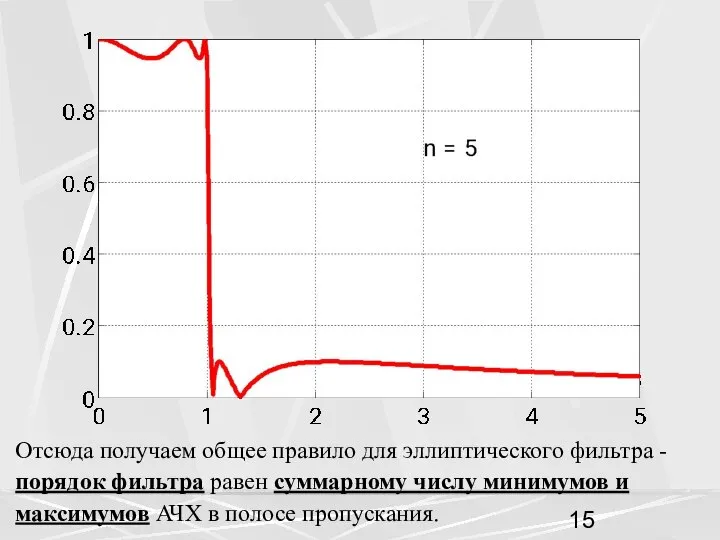
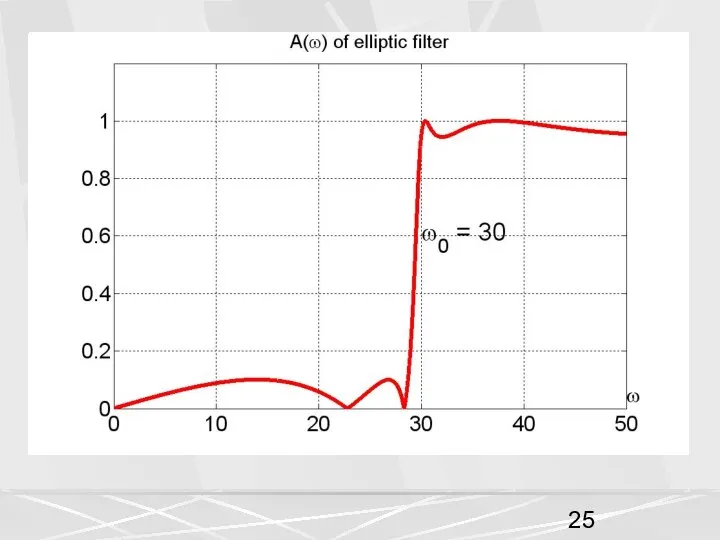
- 12. Здесь выбран интервал от –30 дБ до 5 дБ. Из этого рисунка хороши видно, что уровень
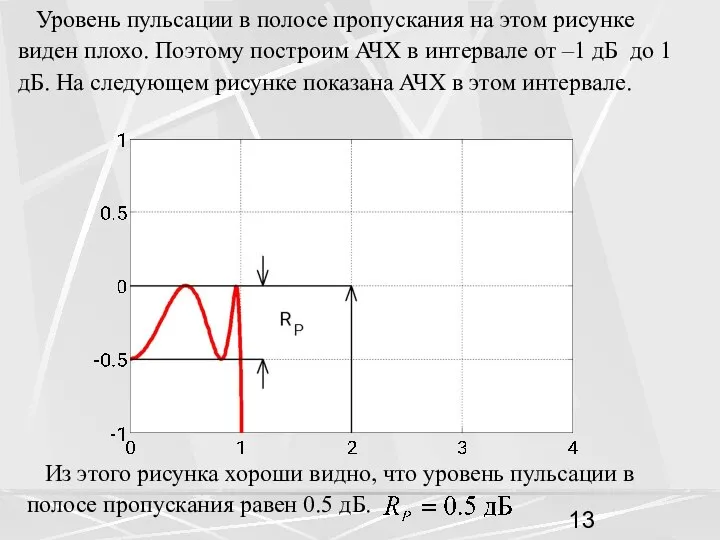
- 13. Уровень пульсации в полосе пропускания на этом рисунке виден плохо. Поэтому построим АЧХ в интервале от
- 15. Отсюда получаем общее правило для эллиптического фильтра - порядок фильтра равен суммарному числу минимумов и максимумов
- 16. Преобразование фильтров Мы рассмотрели несколько известных фильтров – фильтр Баттерворта, фильтр Чебышева первого рода, фильтр Чебышева
- 17. Здесь L(s) – некоторое преобразование. В результате появляется другая передаточная функция. (6) Эта новая передаточная функция
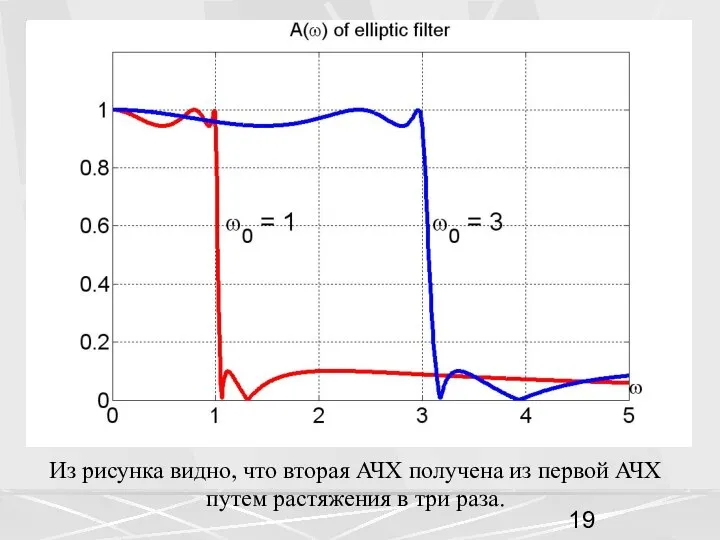
- 18. Изменение частоты среза низкочастотного фильтра ФНЧ Частотную характеристику ФНЧ можно сжимать и растягивать вдоль оси частот
- 19. Из рисунка видно, что вторая АЧХ получена из первой АЧХ путем растяжения в три раза.
- 20. Первый фильтр имеет следующие коэффициенты основного уравнения. b = 0.30 0 0.88 0 0.59 a =
- 23. Преобразование ФНЧ в фильтр высокой частоты ФВЧ Из фильтра низкой частоты можно получить фильтр высокой частоты
- 26. Из рисунков видно, что действительно простое преобразование (8) позволило получить из фильтра низких частот фильтр высоких
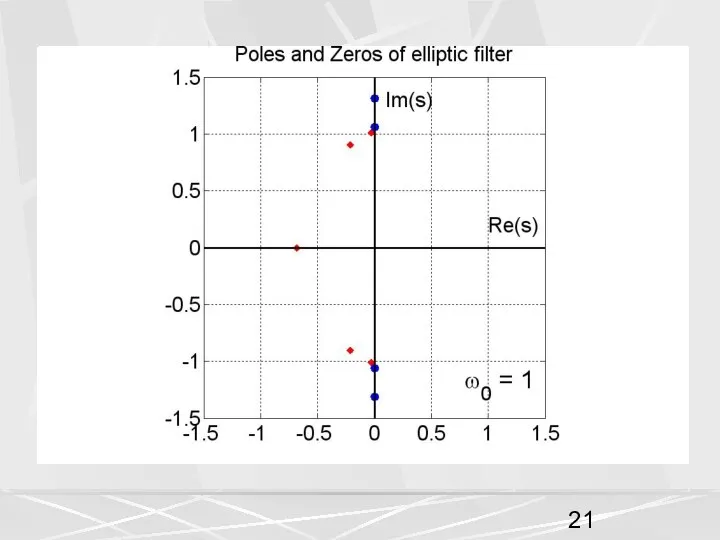
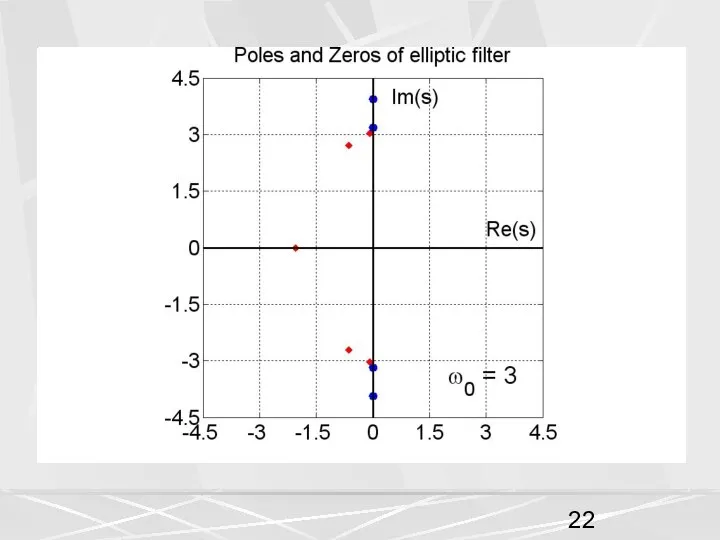
- 29. Первое, на что следует обратить внимание, это то, что число нулей и полюсов осталось прежним, 4
- 30. Преобразование ФНЧ в полосовой фильтр Если использовать более сложное преобразование, чем преобразования (7) и (8), то
- 31. Полосовой фильтр характеризуется нижней границей ω1 полосы пропускания, и верхней границей полосы ω2 пропускания. Параметры преобразования
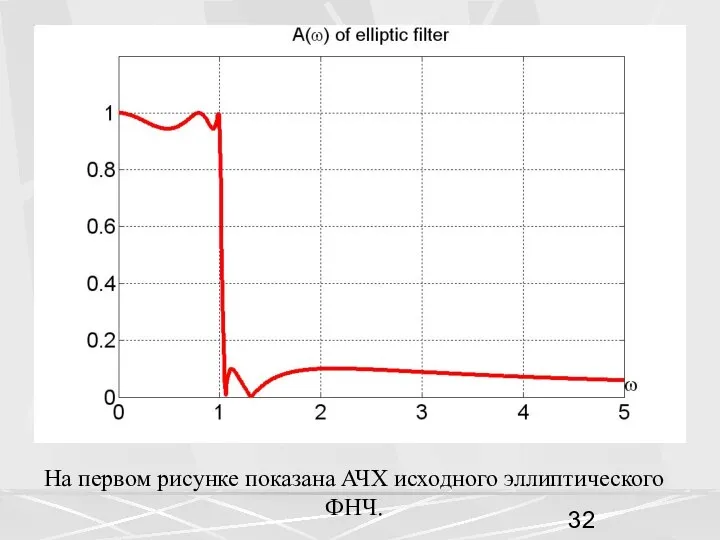
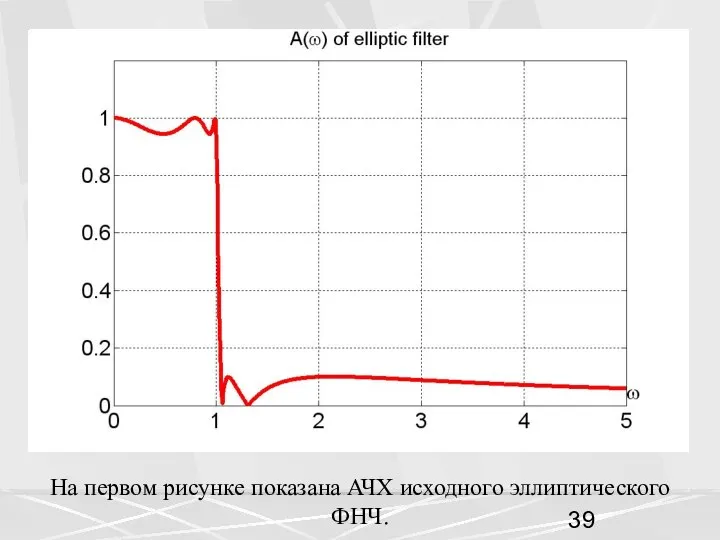
- 32. На первом рисунке показана АЧХ исходного эллиптического ФНЧ.
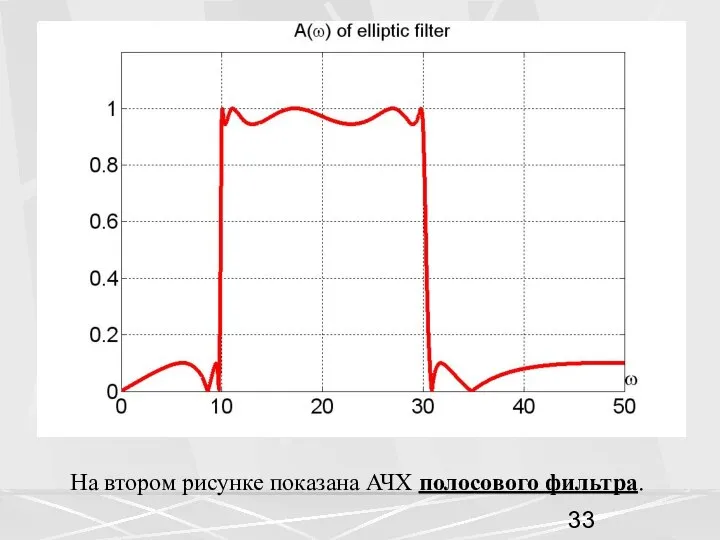
- 33. На втором рисунке показана АЧХ полосового фильтра.
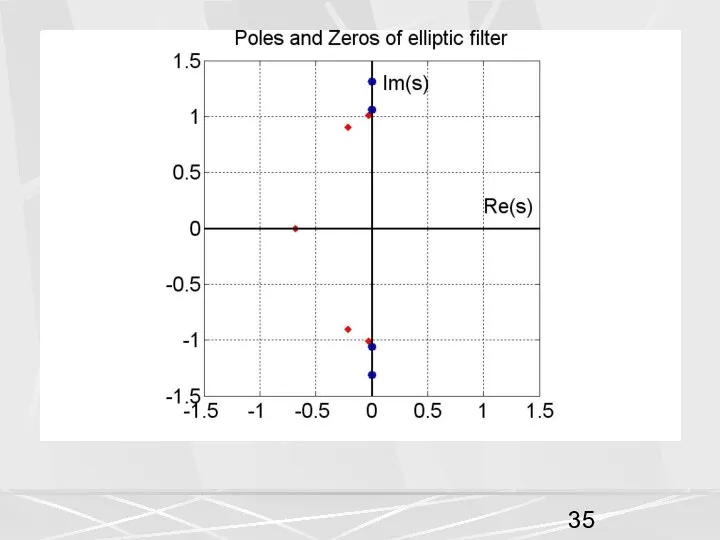
- 34. Из рисунков видно, что преобразование (10) позволило получить из ФНЧ полосовой фильтр. Посмотрим, как изменяются нули
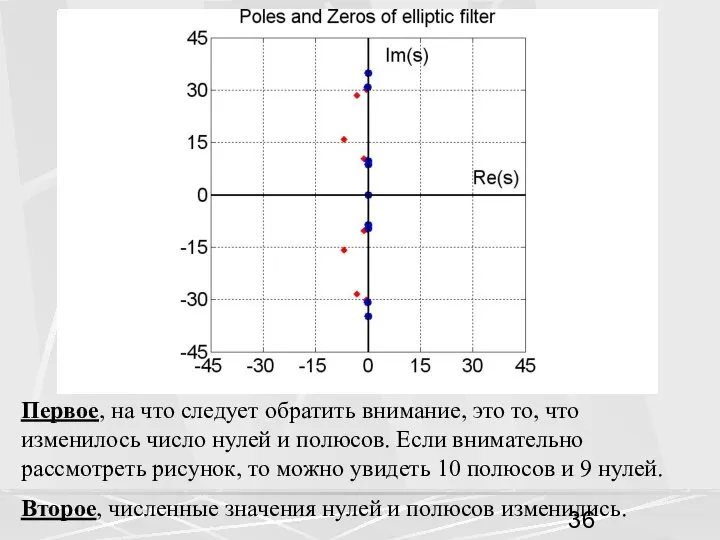
- 36. Первое, на что следует обратить внимание, это то, что изменилось число нулей и полюсов. Если внимательно
- 37. Преобразование ФНЧ в режекторный фильтр Для преобразования фильтра низких частот в режекторный фильтр надо совершить преобразование
- 38. (12) Параметры преобразования (12) связаны с нижней ω1 и верхней ω2 границами полосы задерживания полосового фильтра
- 39. На первом рисунке показана АЧХ исходного эллиптического ФНЧ.
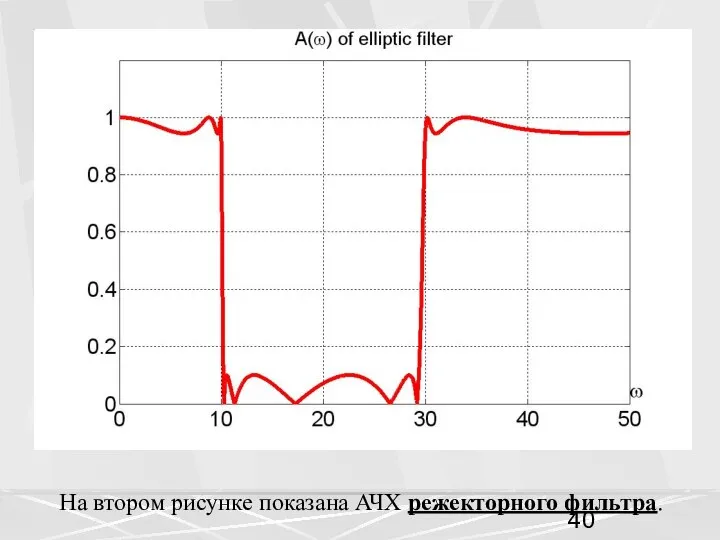
- 40. На втором рисунке показана АЧХ режекторного фильтра.
- 41. Из рисунков видно, что преобразование (12) позволило получить из ФНЧ режекторный фильтр. Посмотрим, как изменяются нули
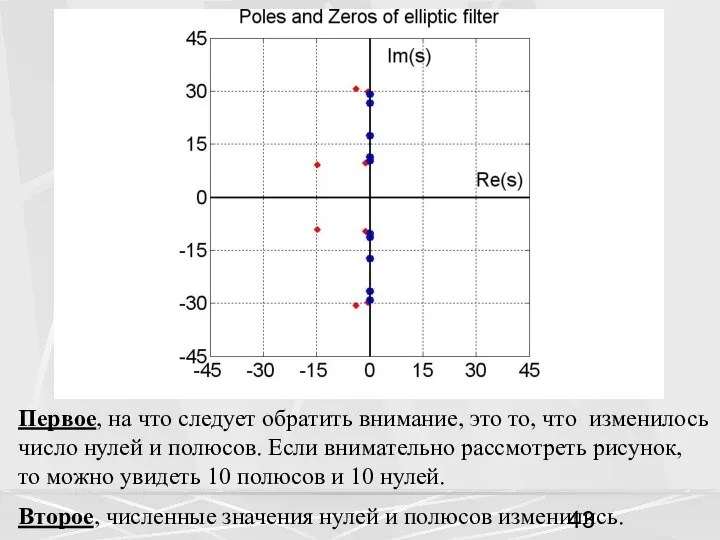
- 43. Первое, на что следует обратить внимание, это то, что изменилось число нулей и полюсов. Если внимательно
- 44. Проектирование дискретных фильтров Под проектированием (или синтезом) цифровых фильтров понимается выбор таких наборов коэффициентов {an} ,{bn}
- 45. Синтез рекурсивного фильтра по аналоговому прототипу Напомним, что если хотя бы один коэффициент an отличен от
- 46. При проектировании дискретного фильтра по аналоговому прототипу необходимо совершить переход из s - области в z
- 47. Основным уравнением аналогового фильтра является следующее дифференциальное уравнение. (14) Аналоговый фильтр описывается также функцией времени h(t)
- 48. Уравнение (15) означает, что выходящий сигнал является сверткой импульсной характеристики и входящего сигнала. Передаточная функция H(s)
- 49. Если заданы коэффициенты bn , an основного уравнения, то передаточная функция определятся следующей формулой. (17) Разложив
- 50. Комплексный коэффициент передачи фильтра является преобразованием Фурье импульсной характеристики. (19) АЧХ и ФЧХ аналогового фильтра определяются
- 51. Теперь рассмотрим дискретные фильтры. Основное разностное уравнение линейного дискретного фильтра имеет вид. (22) Дискретный фильтр описывается
- 52. Уравнение (23) означает, что выходящий сигнал является сверткой импульсной характеристики и входящего сигнала. (24) Передаточная функция
- 53. Если заданы коэффициенты bn , an основного уравнения, то передаточная функция определятся следующей формулой (26) Разложив
- 54. (27) Здесь k = b0 - коэффициент усиления, zi – нули передаточной функции, pi - полюсы
- 55. Здесь Δt - шаг дискретизации, который связан с частотой Найквиста F формулой. (29) АЧХ и ФЧХ
- 56. Сравнение формул для аналогового фильтра и дискретного фильтра показывает, что они во многом близки. Но имеются
- 57. При проектировании дискретного фильтра по аналоговому прототипу необходимо совершить переход из s - области в z
- 58. Метод билинейного - преобразования Данный метод позволяет синтезировать рекурсивный дискретный фильтр по частотной характеристике аналогового прототипа.
- 59. где s определяется билинейным преобразованием (33). Отсюда получаем искомую формулу перехода от аналогового фильтра-прототипа к дискретному
- 60. Объединяя формулы (35) и (36) получаем. Используя формулу Эйлера, получаем. (38) (37) Подставляя выражение (38) в
- 61. (39) Наконец используем связь между комплексным коэффициентом передачи и передаточной функцией аналогового фильтра. (40) Окончательно, объединяя
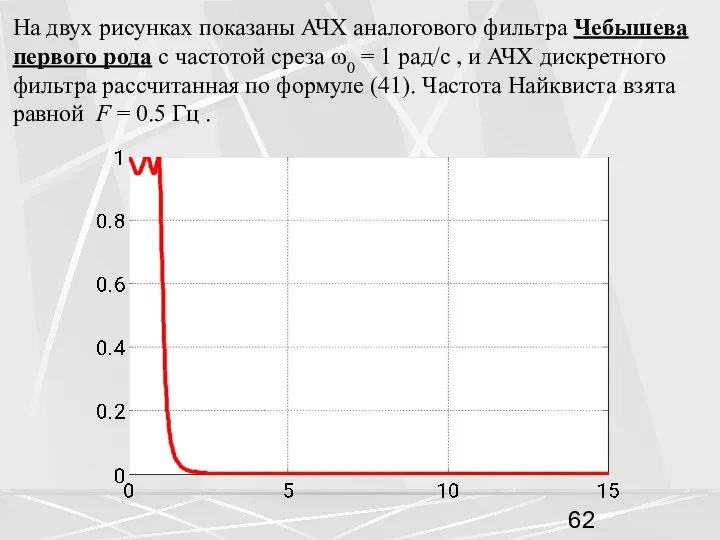
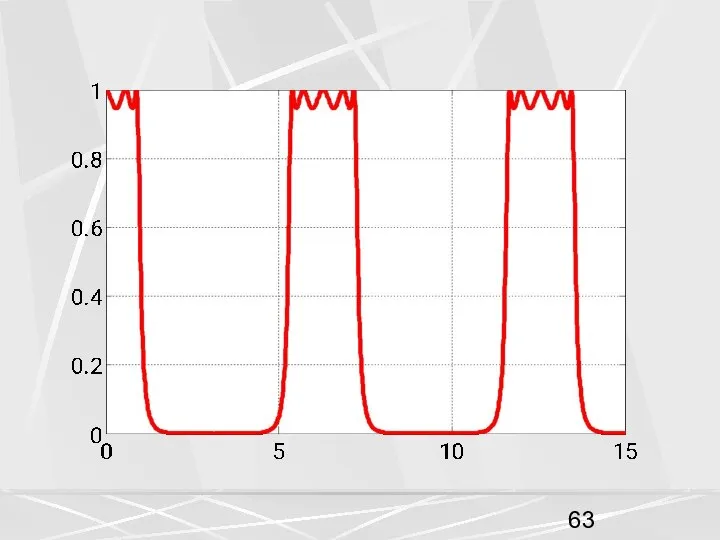
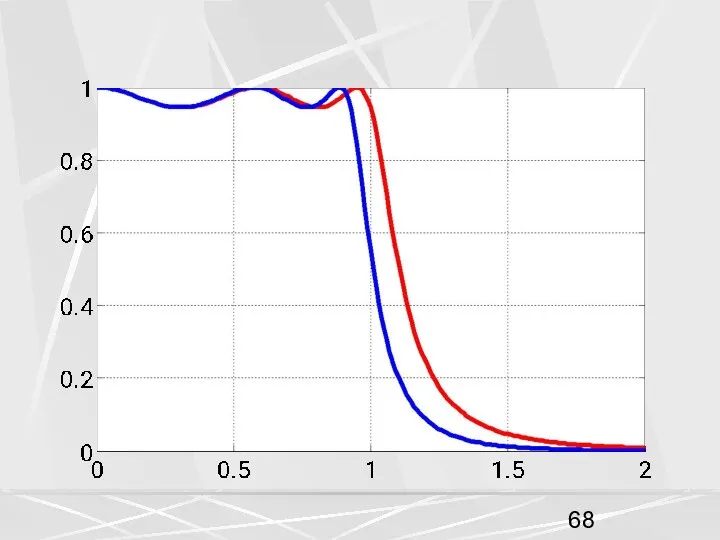
- 62. На двух рисунках показаны АЧХ аналогового фильтра Чебышева первого рода с частотой среза ω0 = 1
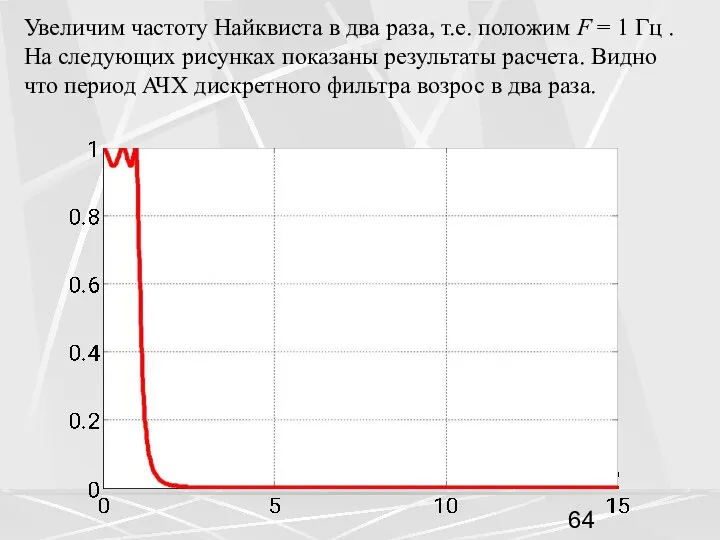
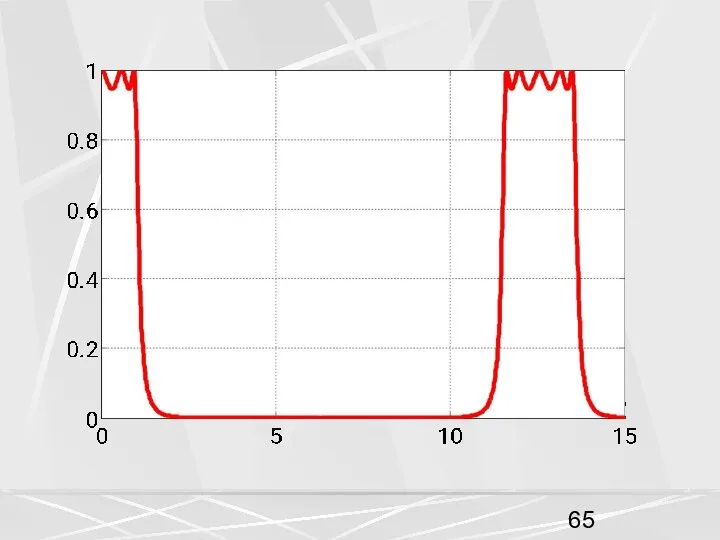
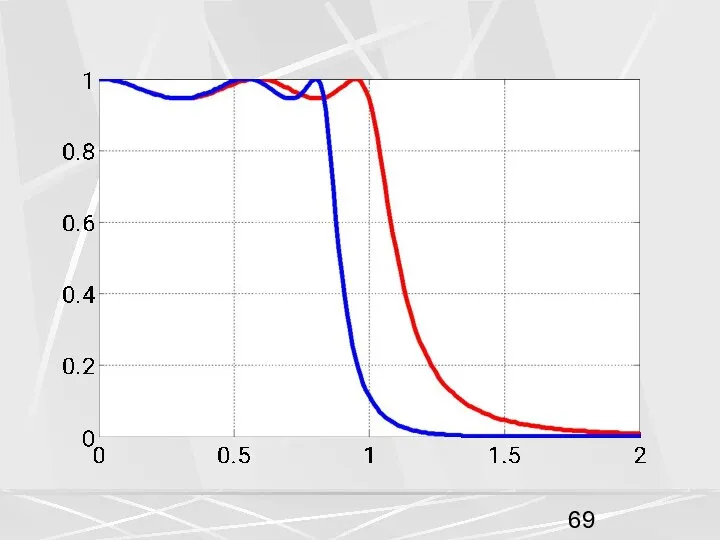
- 64. Увеличим частоту Найквиста в два раза, т.е. положим F = 1 Гц . На следующих рисунках
- 66. Посмотрим на аргумент комплексного коэффициента передачи аналогового фильтра в формуле (41), который обозначим Ω . (42)
- 67. Подставляя (44) в (41) получаем. (45) Поэтому в области низких частот частотные характеристики аналогового и дискретного
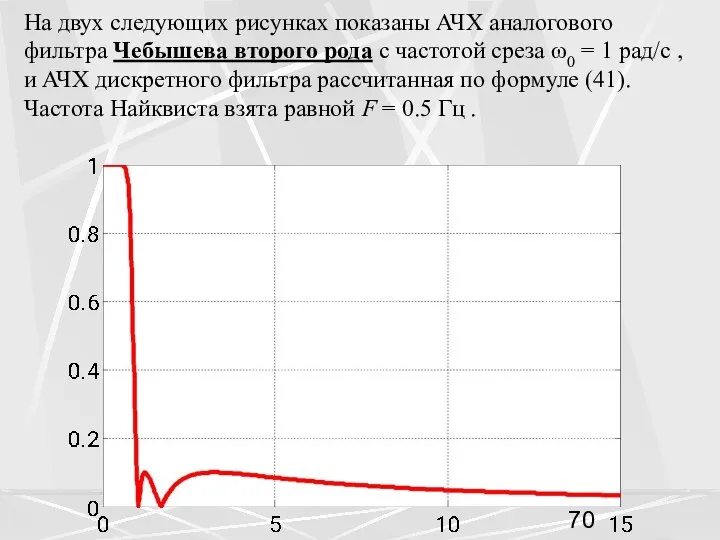
- 70. На двух следующих рисунках показаны АЧХ аналогового фильтра Чебышева второго рода с частотой среза ω0 =
- 72. Скачать презентацию






































 НОВОСТИ Выполнили: Хропина Ольга и Фунтикова Виктория
НОВОСТИ Выполнили: Хропина Ольга и Фунтикова Виктория Мотивационное управление персоналом общеобразовательного учреждения
Мотивационное управление персоналом общеобразовательного учреждения  Компьютерные презентации
Компьютерные презентации  Образ масленицы в народном и изобразительном искусстве. В.И. Суриков «Взятие снежного городка», Б.М.Кустодиев «Масленица».
Образ масленицы в народном и изобразительном искусстве. В.И. Суриков «Взятие снежного городка», Б.М.Кустодиев «Масленица». Функциональная модель коммуникации по Р.О. Якобсону
Функциональная модель коммуникации по Р.О. Якобсону Монтаж сборных строительных конструкций промышленного здания
Монтаж сборных строительных конструкций промышленного здания Решение уравнения с одним неизвестным
Решение уравнения с одним неизвестным  Как прошло лето
Как прошло лето Социально-экономическое развитие ХОРВАТИИ. Выполнила студентка 1 курса группы Т-1207 Пономарева Анна
Социально-экономическое развитие ХОРВАТИИ. Выполнила студентка 1 курса группы Т-1207 Пономарева Анна Thermal radiation
Thermal radiation  Основы радиационной и химической защиты в ЧС
Основы радиационной и химической защиты в ЧС Деление клетки, митоз
Деление клетки, митоз Расчет валов
Расчет валов  Хроническая ИБС
Хроническая ИБС Conseptions of democracy
Conseptions of democracy Презентация Рынок капитала
Презентация Рынок капитала  CКАЗКА «Волшебное число» Эту игру я предлагаю для отработки навыков решения линейных уравнений. Игра ведется на основе сказки об И
CКАЗКА «Волшебное число» Эту игру я предлагаю для отработки навыков решения линейных уравнений. Игра ведется на основе сказки об И Презентация Увеличение таможенных сборов за счет транзитных финансовых потоков
Презентация Увеличение таможенных сборов за счет транзитных финансовых потоков Introduce to Petri nets
Introduce to Petri nets Образ учителя
Образ учителя Основы телекоммуникаций, методы объединения и разделения каналов. (Тема 1.8)
Основы телекоммуникаций, методы объединения и разделения каналов. (Тема 1.8) Memory, Politic and Identity
Memory, Politic and Identity Старинная русская одежда. (4 класс)
Старинная русская одежда. (4 класс) Культура XX века
Культура XX века Ось, знайомтесь - перший клас.
Ось, знайомтесь - перший клас.  Чудеса в исламе
Чудеса в исламе Ремонт тележек грузовых вагонов
Ремонт тележек грузовых вагонов Уголовное право
Уголовное право