Содержание
- 2. Метод проекции градиента является обобщением метода наискорейшего спуска на случай, когда решается задача минимизации нелинейной функции
- 3. 1. Стартовую точку выбираем произвольно Линии равного уровня критерия Минимум 90° 2. Определяем направление антиградиента и
- 4. Рассмотрим, какие изменения нужно внести в метод наискорейшего спуска, чтобы распространить его на задачи с ограничениями
- 5. Найдем направление антиградиента. Перемещение по этому направлению невозможно. Поэтому выберем из числа возможных такое, перемещение в
- 7. Скачать презентацию
Метод проекции градиента является обобщением метода наискорейшего спуска на случай, когда
Метод проекции градиента является обобщением метода наискорейшего спуска на случай, когда
Хотя метод применим и в задачах с нелинейными ограничениями, хорошая сходимость имеет место только в случае, когда ограничения – линейны.
Постановка задачи: найти x (n-мерный вектор) , доставляющий минимум выпуклой скалярной функции f(x) при условиях: A1x = B1, A2x ≤ B2
Примечание: Если должна быть учтена неотрицательность х, то, в отличие от ЛП, ограничения х≥0 должны быть включены в общую систему ограничений в форме -х ≤ 0.
Напомним основные позиции метода наискорейшего спуска (поиск минимума выпуклой функции f(x) без ограничений)
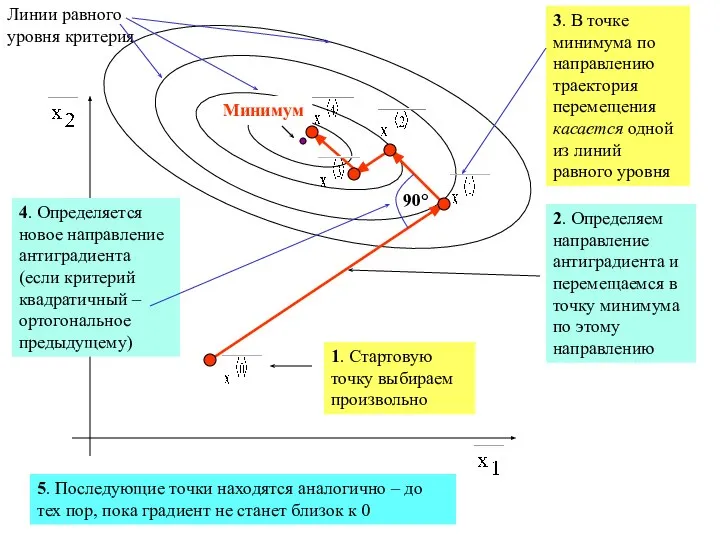
1. Стартовую точку выбираем произвольно
Линии равного уровня критерия
Минимум
90°
2. Определяем направление антиградиента
1. Стартовую точку выбираем произвольно
Линии равного уровня критерия
Минимум
90°
2. Определяем направление антиградиента
3. В точке минимума по направлению траектория перемещения касается одной из линий равного уровня
4. Определяется новое направление антиградиента (если критерий квадратичный – ортогональное предыдущему)
5. Последующие точки находятся аналогично – до тех пор, пока градиент не станет близок к 0
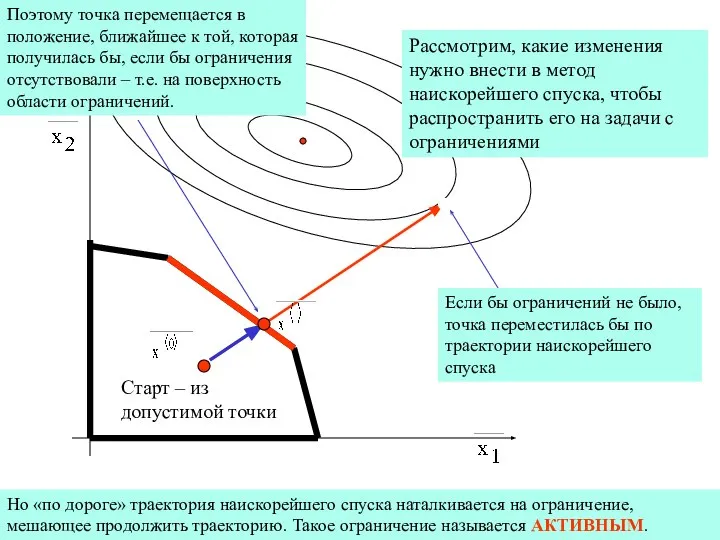
Рассмотрим, какие изменения нужно внести в метод наискорейшего спуска, чтобы распространить
Рассмотрим, какие изменения нужно внести в метод наискорейшего спуска, чтобы распространить
Старт – из допустимой точки
Если бы ограничений не было, точка переместилась бы по траектории наискорейшего спуска
Но «по дороге» траектория наискорейшего спуска наталкивается на ограничение, мешающее продолжить траекторию. Такое ограничение называется АКТИВНЫМ.
Поэтому точка перемещается в положение, ближайшее к той, которая получилась бы, если бы ограничения отсутствовали – т.е. на поверхность области ограничений.
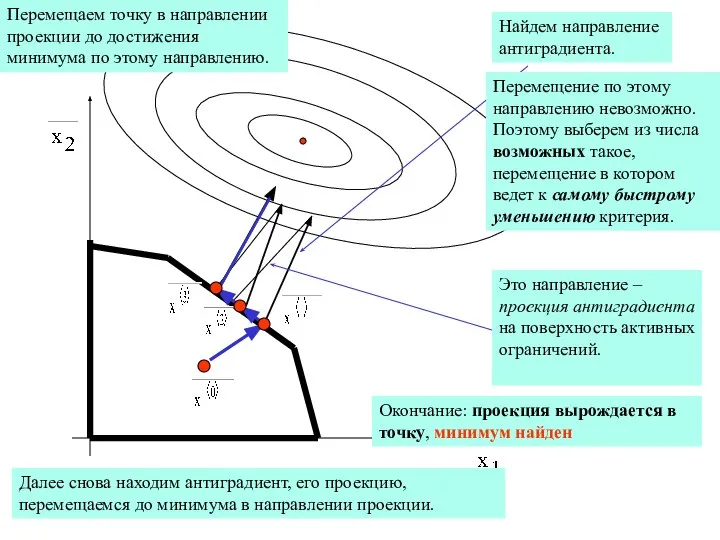
Найдем направление антиградиента.
Перемещение по этому направлению невозможно. Поэтому выберем из
Найдем направление антиградиента.
Перемещение по этому направлению невозможно. Поэтому выберем из
Это направление – проекция антиградиента на поверхность активных ограничений.
Перемещаем точку в направлении проекции до достижения минимума по этому направлению.
Далее снова находим антиградиент, его проекцию, перемещаемся до минимума в направлении проекции.
Окончание: проекция вырождается в точку, минимум найден

 Деформация растяжения
Деформация растяжения Преимущества технологии баз данных
Преимущества технологии баз данных Команды языка Паскаль
Команды языка Паскаль Шифрование в цифровой и аналоговой телефонии
Шифрование в цифровой и аналоговой телефонии Биполярные транзисторы
Биполярные транзисторы Индексы
Индексы Технологическая карта - способ проектирования урока в системно-деятельностном подходе. Кинчина Наталия Олеговна учитель начальн
Технологическая карта - способ проектирования урока в системно-деятельностном подходе. Кинчина Наталия Олеговна учитель начальн Многопроцессорные системы (продолжение). Графические ускорители. (Лекция18)
Многопроцессорные системы (продолжение). Графические ускорители. (Лекция18) Потребности
Потребности Структура курса дисциплины «Культурология»
Структура курса дисциплины «Культурология» Предмет информатика
Предмет информатика Хранимые процедуры и триггеры
Хранимые процедуры и триггеры Праздники и искусство в жизни человека
Праздники и искусство в жизни человека Спортивная подготовка в художественной гимнастике
Спортивная подготовка в художественной гимнастике Резание металла
Резание металла Motronic
Motronic Определение биохимии История развития биохимии Понятие «жизнь» Живой организм Строение и функции белков
Определение биохимии История развития биохимии Понятие «жизнь» Живой организм Строение и функции белков  Предшественники античной культуры (III тысячи лет до н.э. – 200 лет н.э.)
Предшественники античной культуры (III тысячи лет до н.э. – 200 лет н.э.) Золотодобывающая промышленность России Выполнил: студент ФТД-4, группы Т093, Воробьев Дм.Ник.
Золотодобывающая промышленность России Выполнил: студент ФТД-4, группы Т093, Воробьев Дм.Ник. Grammar Bank_test 8
Grammar Bank_test 8 Предложения с глаголом 是
Предложения с глаголом 是 Интерфейсы: interface IMy
Интерфейсы: interface IMy Жизнь и творчество Владимира Владимировича Набокова (1899-1977)
Жизнь и творчество Владимира Владимировича Набокова (1899-1977) системная ПРОТИВОВОСПАЛИТЕЛЬНАЯ ТЕРАПИЯ
системная ПРОТИВОВОСПАЛИТЕЛЬНАЯ ТЕРАПИЯ Применение БПЛА в картографии
Применение БПЛА в картографии Август Шлейхер. Натуралистическое направление
Август Шлейхер. Натуралистическое направление Современные технические средства аудио- и визуального контроля и их использование в органах внутренних дел Российской Федерации
Современные технические средства аудио- и визуального контроля и их использование в органах внутренних дел Российской Федерации Тригонометрические уравнения
Тригонометрические уравнения