Геометрический смысл уравнения первой степени
Аналогично для неравенства
ax+by+c≥0. (2)
Если b≠0, то данное
неравенство приводится к одному из видов у≥kх+p или у≤kх+р.
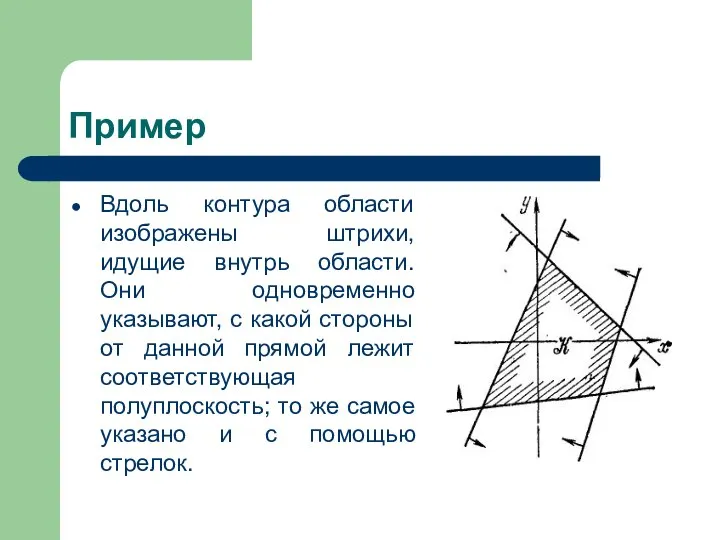
Первому из этих неравенств удовлетворяют все точки, лежащие «выше» прямой у=kх+р или же на этой прямой, а второму – все точки, лежащие «ниже» прямой у=kх+р или на этой прямой.
Если же b=0, то неравенство приводится к одному из видов х≥h или х≤h. Первому из них удовлетворяют все точки, лежащие «правее» прямой х=h или на этой прямой, второму – все точки, лежащие «левее» прямой х=h или на этой прямой.






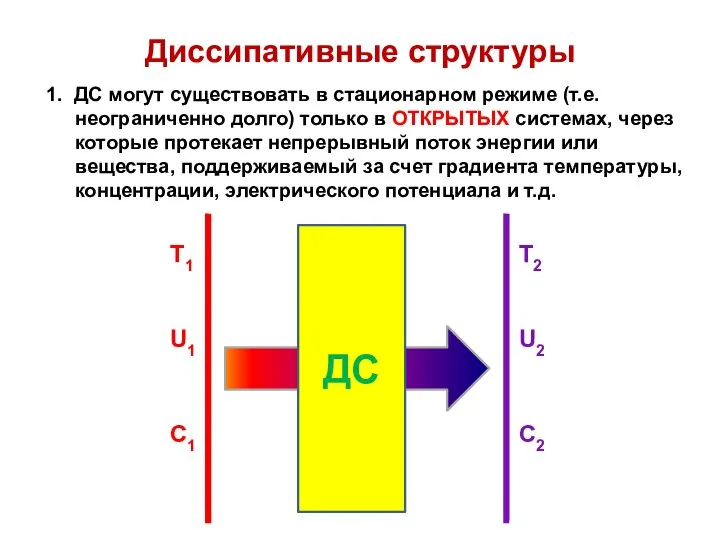 Диссипативные структуры
Диссипативные структуры селянської реформи 1861 року
селянської реформи 1861 року  Презентация "Славянские земледельческие обряды" - скачать презентации по МХК
Презентация "Славянские земледельческие обряды" - скачать презентации по МХК Презентация дисциплины Коррекционная педагогика
Презентация дисциплины Коррекционная педагогика Вступ. Культура як суспільне явище
Вступ. Культура як суспільне явище Архитектура Московского Кремля
Архитектура Московского Кремля Un usual kinds of sport un
Un usual kinds of sport un Устройство нановесы
Устройство нановесы Спорт төрҙәре
Спорт төрҙәре Искусство Индии Восток, Древность,Современость
Искусство Индии Восток, Древность,Современость История кинематографа Материалы к уроку изобразительного искусства в 9 классе по программе Б.Неменского
История кинематографа Материалы к уроку изобразительного искусства в 9 классе по программе Б.Неменского  УСЛОВНО-ПАТОГЕННЫЕ МИКРООРГАНИЗМЫ
УСЛОВНО-ПАТОГЕННЫЕ МИКРООРГАНИЗМЫ  Золушка Художник Сергий Елена
Золушка Художник Сергий Елена  Расчет пластин
Расчет пластин Принципы и методы управления. Принятие управленческих решений
Принципы и методы управления. Принятие управленческих решений Презентация Культура делового общения
Презентация Культура делового общения Изменение политической системы СССР в 1953-1964 гг
Изменение политической системы СССР в 1953-1964 гг Урок обучения чтению Тема : чтение слов и предложений с буквой «Й» Учитель начальных классов ГКОУ «Кабанская СКОШИ VIII» Панфилова
Урок обучения чтению Тема : чтение слов и предложений с буквой «Й» Учитель начальных классов ГКОУ «Кабанская СКОШИ VIII» Панфилова  Воры в законе
Воры в законе Презентация Режим государственной границы
Презентация Режим государственной границы  Пермская и Кунгурская епархия РПЦ Добрянское благочиние. Храм св.апостола Иоанна Богослова
Пермская и Кунгурская епархия РПЦ Добрянское благочиние. Храм св.апостола Иоанна Богослова Сердечно-сосудистая система
Сердечно-сосудистая система  «ПОМНИ ПРАВИЛА ДВИЖЕНЬЯ КАК ТАБЛИЦУ УМНОЖЕНЬЯ»
«ПОМНИ ПРАВИЛА ДВИЖЕНЬЯ КАК ТАБЛИЦУ УМНОЖЕНЬЯ»  Дом из газобетона
Дом из газобетона Поддержка за пару минут makedreamprofits.ru
Поддержка за пару минут makedreamprofits.ru Подшипники скольжения
Подшипники скольжения С П О СО Б Ы О Б Р А З О В А Н И Я С У Щ Е С Т В И Т Е Л Ь Н Ы Х
С П О СО Б Ы О Б Р А З О В А Н И Я С У Щ Е С Т В И Т Е Л Ь Н Ы Х Что такое ООП и с чем его едят
Что такое ООП и с чем его едят