Методы анализа линейных электрических цепей

3.1. Основные принципы, теоремы и преобразования линейных электрических цепей
3.2. Методы анализа

3.1. Основные принципы, теоремы и преобразования линейных электрических цепей

Принципы (свойства).
1.Принцип наложения

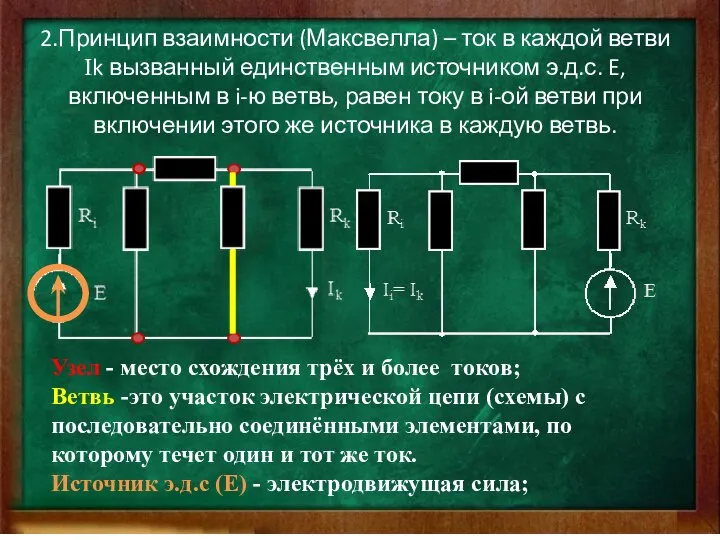
2.Принцип взаимности (Максвелла) – ток в каждой ветви Ik вызванный единственным

3.Принцип линейности – две любые величины (токи и напряжения) двух любых

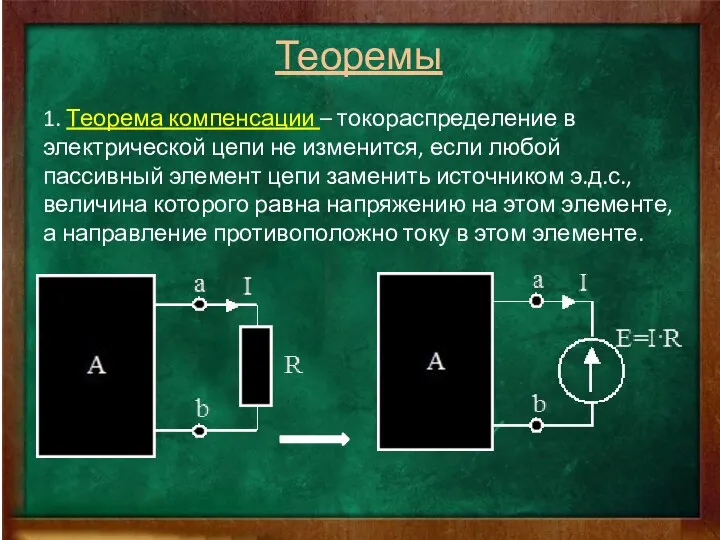
Теоремы

1. Теорема компенсации – токораспределение в электрической цепи не изменится, если

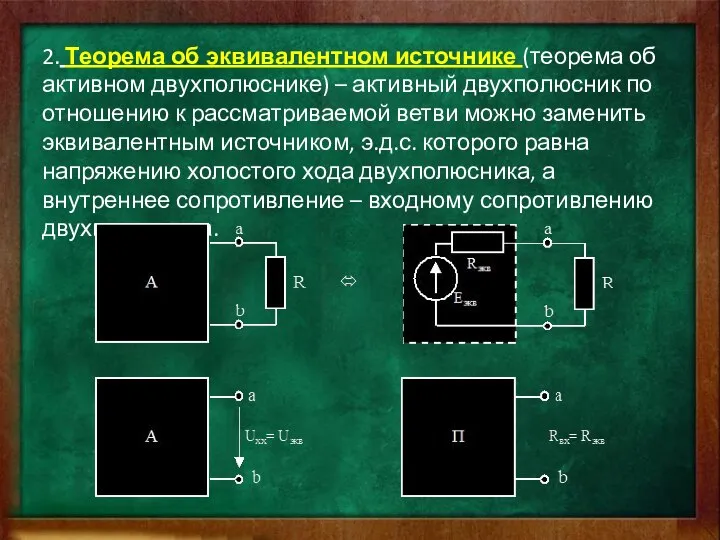
2. Теорема об эквивалентном источнике (теорема об активном двухполюснике) – активный

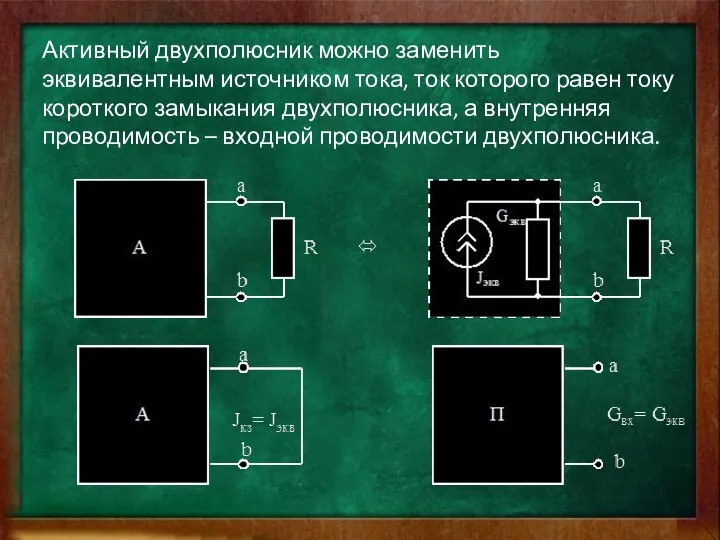
Активный двухполюсник можно заменить эквивалентным источником тока, ток которого равен току

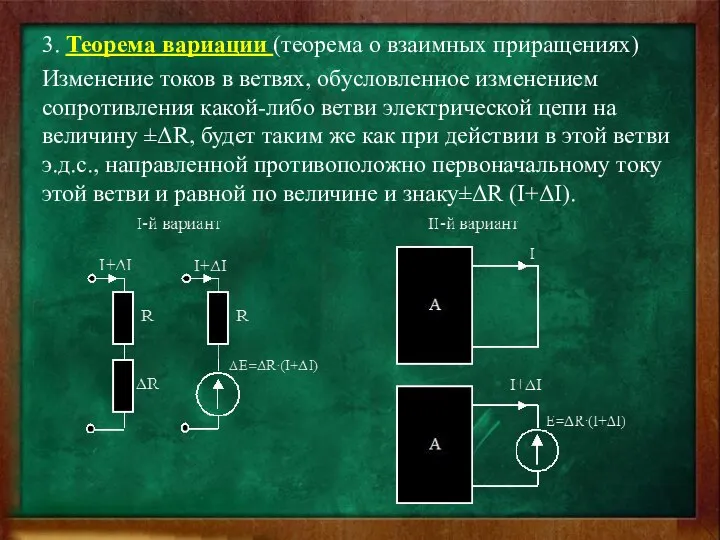
3. Теорема вариации (теорема о взаимных приращениях)
Изменение токов в ветвях, обусловленное

Эквивалентные преобразования
1. Преобразование звезда - треугольник Y⇒∇ и треугольник - звезда

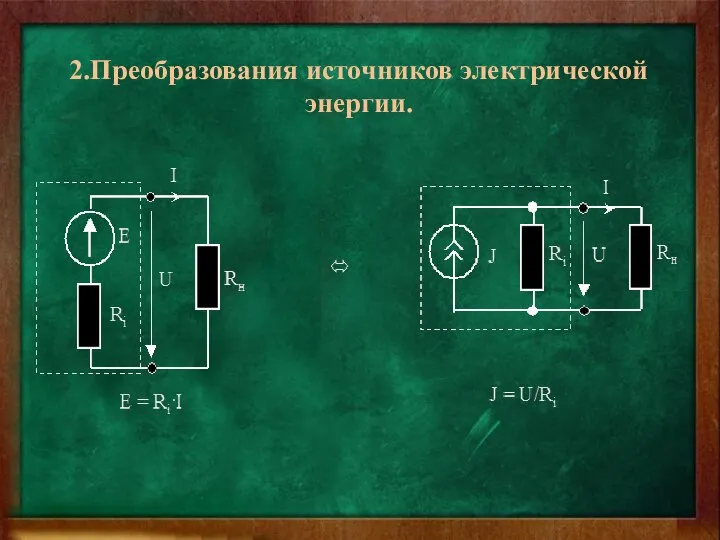
2.Преобразования источников электрической энергии.

3.2. Методы анализа резистивных цепей по уравнениям.
Линейные цепи – параметры (R,

3.2.1. Анализ линейных электрических цепей постоянного тока.
Постоянный ток – неизменный по

Алгоритм расчета
1.Путем последовательных упрощений с помощью эквивалентных преобразований рассчитывают эквивалентное сопротивление

Примечание

1.Если цепь питается от источника тока, то расчет ведут по п.(3,

;

;

;

;

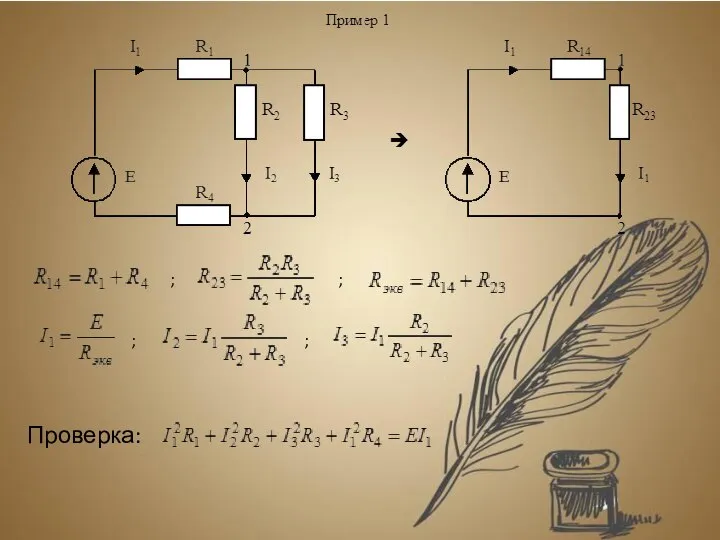
Проверка:

3.2.2. Метод непосредственно применения законов Кирхгофа.

Алгоритм расчета.
Выбирают произвольное положительное направление искомых

2. Составляют уравнение по 1-му закону Кирхгофа для (y-1) узлов схемы,

3. Составляют [(в - вит) - (у - 1)] уравнений по

3.2. Выбирают положительное направление обхода контуров (обычно по часовой стрелке).
3.3. При

4.Решают тем или иным методом полученную систему линейных алгебраических уравнений.
В рассматриваемом

3.2.3. Метод контурных токов
Метод основан на введении промежуточной неизвестной величины –

Алгоритм расчета (после вывода расчетных уравнений по 2 закону Кирхгофа):
1.Проставляют направления

2.Для каждого независимого контура (ячейки) составляют расчетное контурное уравнение согласно правилу:

Примечание
При наличии ветвей с источниками тока либо источники тока преобразуют в

3.Решают тем или иным методом полученную систему линейных алгебраических уравнений.
4.На основании

3.2.4. Метод узловых потенциалов
Метод основан на введении промежуточной неизвестной величины –

Алгоритм расчета (после вывода расчетных уравнений по 1-му закону Кирхгофа):
1.Принимают потенциал

2.Составляют уравнение для каждого из оставшихся (y-1) узлов согласно правилу: левая

Примечание
При наличии ветвей с источником тока необходимо учесть следующее:
-проводимость ветви с

3.Решают тем или иным способом полученную систему линейных алгебраических уравнений.
4.На основании

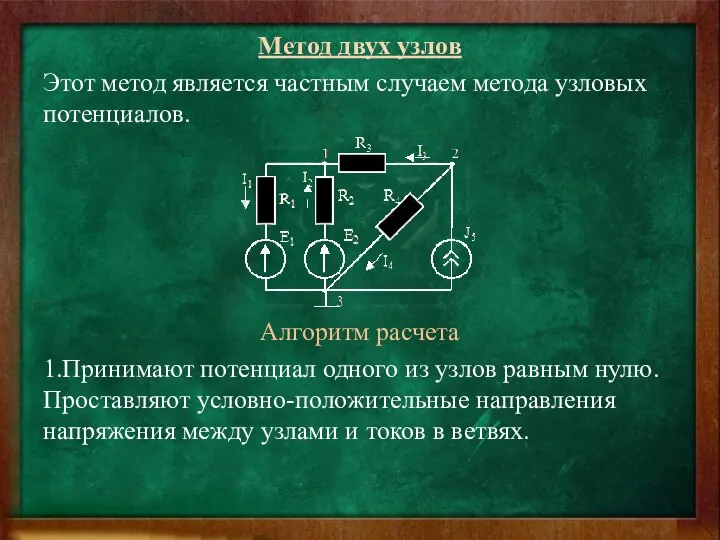
Метод двух узлов
Этот метод является частным случаем метода узловых потенциалов.
Алгоритм расчета
1.Принимают

2.Определяют величину и реальное положительное направление напряжения между узлами по формуле:
При

3.2.5. Метод суперпозиции (наложения)
Метод наложения основывается на общефизическом принципе независимости действия

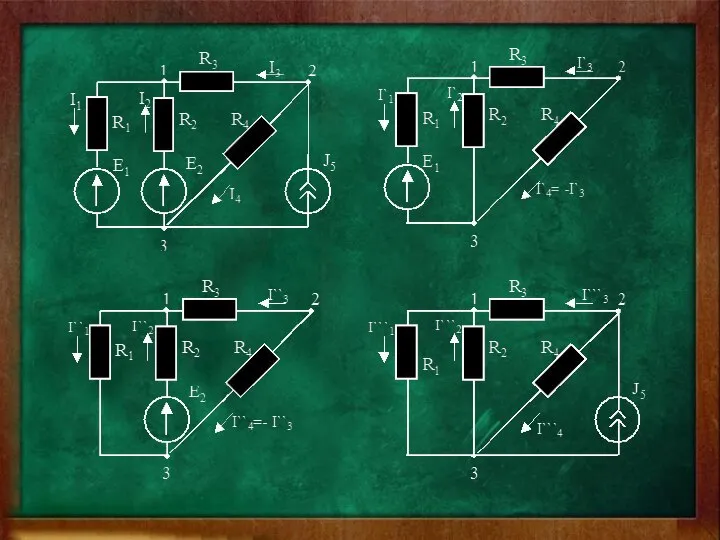
Алгоритм расчета
1.Рассчитывают величину и направление частичных токов во всех ветвях электрической

2.Находят величины и направления токов в ветвях путем алгебраического сложения частичных

3.2.6. Метод эквивалентного генератора
Метод основан на замене активного двухполюсника эквивалентным генератором

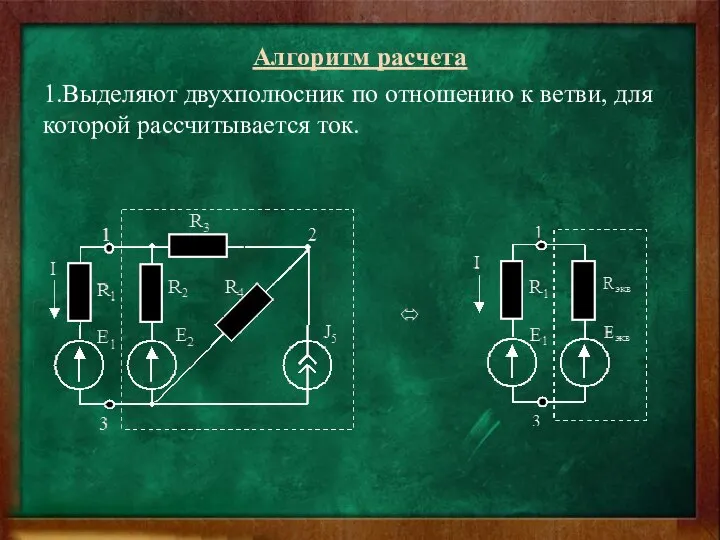
Алгоритм расчета
1.Выделяют двухполюсник по отношению к ветви, для которой рассчитывается ток.

2.Тем или иным методом рассчитывают величину и полярность напряжения на зажимах

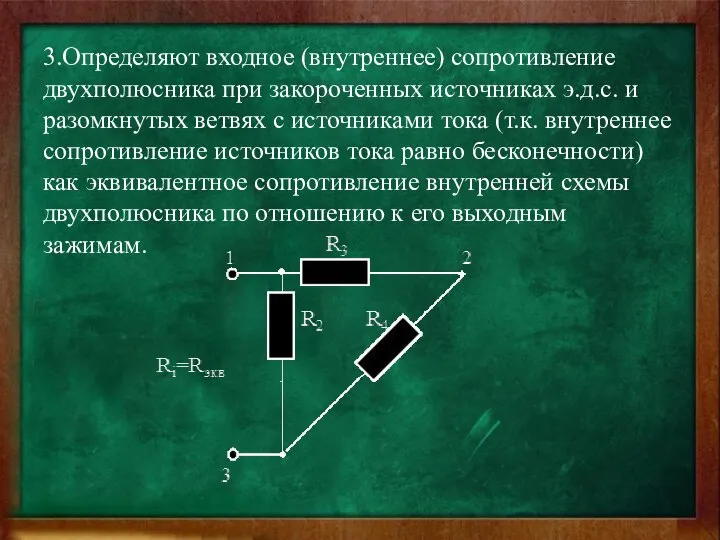
3.Определяют входное (внутреннее) сопротивление двухполюсника при закороченных источниках э.д.с. и разомкнутых

4.Рассчитывают искомый ток ветви
5.Метод эквивалентного генератора эффективен при опытном определении входного

3.3. Матричные методы анализа электрических цепей.
Рассмотренные ранее методы анализа сложных цепей

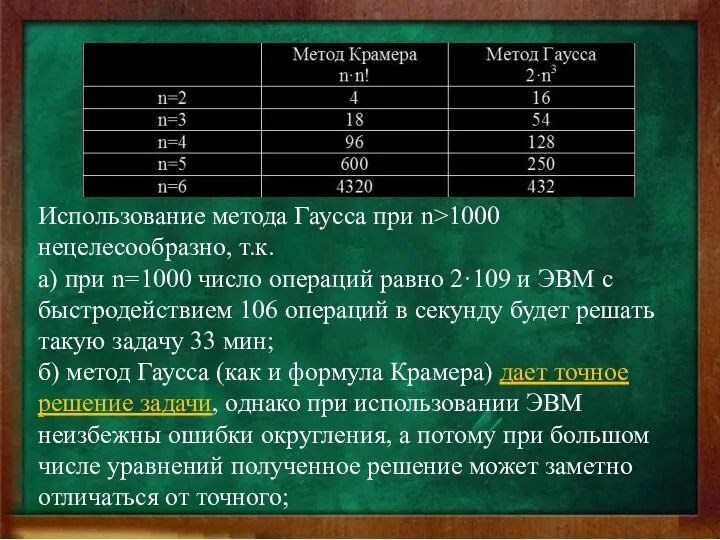
Использование метода Гаусса при n>1000 нецелесообразно, т.к.
а) при n=1000 число операций

в) существенным параметром вычислительного процесса является и число используемых ячеек памяти,

Матрица – совокупность величин (элементов), расположенных в виде прямоугольной таблицы.
Математическая символика

4) Решение системы уравнений в матричной форме сводится к нахождению обратной

Пример:
?
[R] x [I] = [E] ?
[I] = [R]-1 [E]

3.3.1. Матрично-топологический метод анализа электрических цепей
Свойства любой электрической цепи определяются ее

Свойства графа, а, следовательно, свойства структуры электрической цепи, могут быть описаны

Основные топологические понятия и определения.
Топология – изучение свойств любой электрической цепи

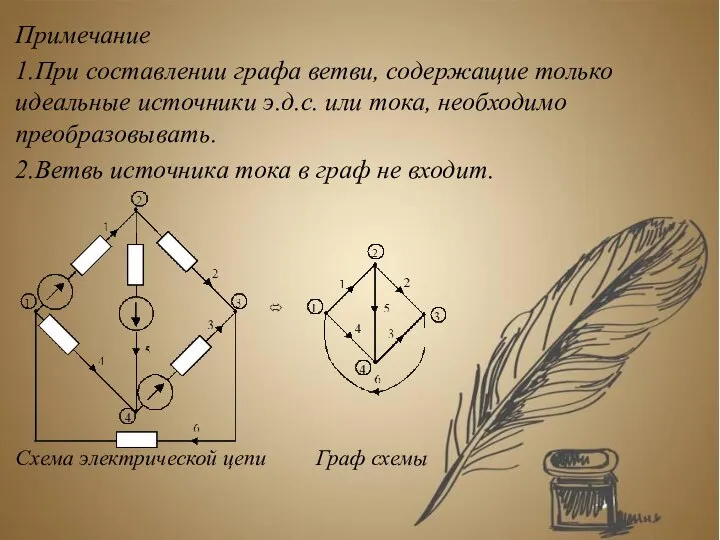
Примечание
1.При составлении графа ветви, содержащие только идеальные источники э.д.с. или тока,

Подграф схемы – часть графа схемы: дерево, связи, главный контур, главное

Нумерация главных контуров определяется нумерацией входящих в них ветвей связи.
За положительное

Сечение графа – поверхность, охватывающая совокупность узлов и ветвей графа и

Топологические матрицы
Структура графа может быть описана в алгебраической форме, в виде

Матрица соединений (узловая, структурная)
Для описания структуры графа в алгебраической форме, составим

Узел, соответствующий вычеркнутой строке – базисный. Полученная матрица – узловая, независимая
–

3.3.2. Метод непосредственного применения законов Кирхгофа в матрично-топологической форме
Запись 1-го закона

Для описания этих законов в топологической форме вводят понятия матриц-столбцов токов

Согласно 1-му закона Кирхгофа эта сумма равна 0, т.е. полученное матричное

Матрица источников тока – столбцовая, число строк которой равно числу ветвей

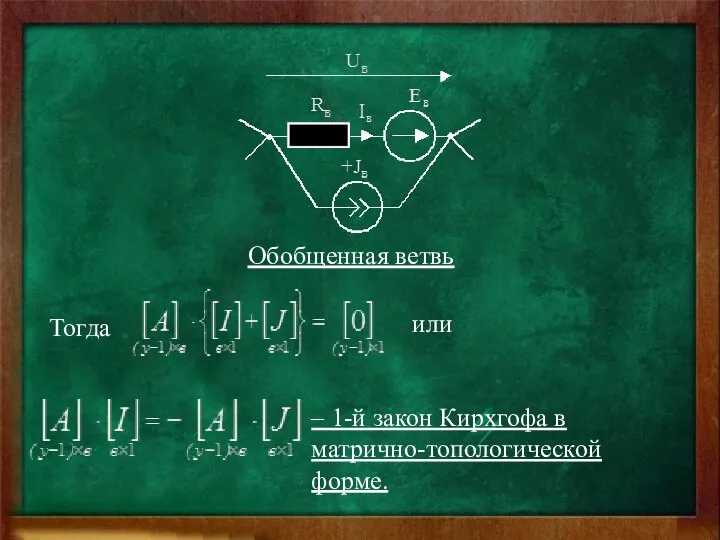
Обобщенная ветвь

Тогда

или

– 1-й закон Кирхгофа в матрично-топологической форме.

Контурная матрица.
Независимые контуры – контуры, в каждый из которых входит только

Контурные матрицы контуров составляют для независимых контуров выбранного дерева.
Число строк контурной

– ставят (+1), если направление стрелки на какой-либо ветви этого контура

Запись 2-го закона Кирхгофа с помощью топологических матриц.
Если перемножить контурную матрицу

Матрица э.д.с. – столбцовая матрица, число строк которой равно числу ветвей

Матрица сопротивлений ветвей – квадратная, по её диагонали записывают собственные сопротивления

Алгоритм расчета электрической цепи по законам Кирхгофа в матрично-топологической форме:
1.Выбирают произвольное

Матрицу токов источников тока:
Матрицу сопротивления ветвей:

3.Изображают граф схемы электрической цепи и одно из деревьев графа и

3.3.3. Матрично-топологическая форма метода контурных токов
Для одного из деревьев графа вводятся

Можно показать, что матрица-столбец токов ветвей [I] может быть записана через

или
где
– квадратная матрица контурных сопротивлений: по диагонали собственные сопротивления контуров, остальные

Алгоритм расчета электрической цепи по методу контурных токов в матрично-топологической форме:
1.Выбирают

3.3.4. Матрично-топологическая форма метода узловых потенциалов.
 Можно показать, что матрица напряжений обобщенных

где [Gу] – квадратная матрица узловых проводимостей
[Iу] – матрица–столбец узловых токов.
Тогда,

При этом

Алгоритм расчета электрической цепи по методу узловых потенциалов в матрично-топологической форме:
1.