Содержание
- 2. 1.Элементарные функции Степенная Y=Xn Показательная Y=aX Логарифмическая Y=logaX Тригонометрические Y=sinX; Обратные тригонометрические функции Y=arcsinX…. Элементарными функциями
- 3. 1.Предельные величины в экономике Теоретический анализ разнообразных явлений экономики использует ряд предельных величин. Основными являются: предельные
- 4. Предельные величины в экономике Пусть q - количество произведенной продукции, C(q) - издержки соответствующие данному выпуску.
- 5. Предельные величины в экономике Пример. Пусть C(q) = 1500q - 2q2 + 0,002q3. Тогда дополнительные издержки,
- 6. 2.Эластичность и ее свойства Для исследования предельных величин используется понятие эластичности. Понятие эластичности было введено Аланом
- 7. Эластичность Определение. Эластичностью функции у = f(x) в точке х0 называется предел Eyx(x0) = lim [(Δy/y]
- 8. Эластичность Если ясно, в какой точке определяется эластичность и какая переменная является независимой, то могут опускаться
- 9. Эластичность Т.О. эластичность Еу - это коэффициент пропорциональности между относительными изменениями величин у и х. Если,
- 10. Свойства эластичности 1. Эластичность в точке х0 суммы y=y1+...+yn положительных функций Yi=fi(X) (i= 1, 2, ...,
- 11. Свойства эластичности 2. Эластичность произведения функций U = U(х) и V = V(x) в точке X0
- 12. Свойства эластичности 3. Эластичность частного функций и = и(х) и v = v(x) в точке х0
- 13. Свойства эластичности 4. Для функций у =f(x) и х = g(t) эластичность у по t в
- 14. Задания: Найти эластичность функции y=C – const Найти эластичность функции y=x+C Найти эластичность функции y=xa
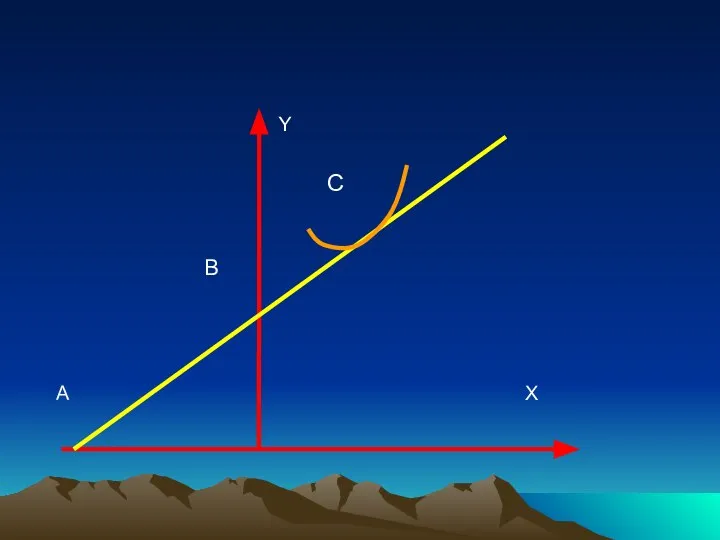
- 15. Геометрический смысл эластичности. Геометрический смысл производной: f'(x0) - это тангенс угла наклона касательной к графику функции
- 17. Если эластичность Y по X положительна, то она совпадает с отношением длин отрезков BC и АС
- 18. 3.Ценовая эластичность спроса. Пусть D = D(p) - спрос (в натуральных единицах) на некоторый товар при
- 19. Совершенно неэластичный спрос Термин означает крайний случай, когда изменение цены не приводит ни к какому изменению
- 20. Эластичность спроса Если имеется достаточный запас товара, то D = D(p) – то он характеризует количество
- 21. Вывод Если спрос эластичен, то изменение цены вызывает изменение общей выручки в противоположном направлении. Если же
- 22. Цена, предельные издержки и объем производства Пусть q - выпуск продукции (в натуральных единицах); R(q) -выручка
- 23. Цена, предельные издержки и объем производства 1)Функции R(q),C(q) определены на полуинтервале [0, +∞) и дифференцируемы при
- 24. Цена, предельные издержки и объем производства Пусть условия 1), 2) выполнены. Тогда функция П(q) = R(q)
- 25. Цена, предельные издержки и объем производства В экономической теории равенство объясняется как правило, согласно которому фирма,
- 26. 4. Задачи оптимального потребительского выбора Пусть х - количество единиц первого продукта в наборе, у -
- 27. Функцией полезности U(x,y) называется функция, задающая степень полезности набора товаров, состоящего из х единиц товара Х
- 28. Данная функция удовлетворяет следующим условиям: 1. Для любых двух наборов товаров X и Y , таких,
- 29. Теорема Дебре Для стандартных предпочтений потребителя всегда можно построить функцию полезности.
- 30. Основные виды функций полезности
- 31. Данное семейство функций полезности описывает предпочтения потребителя соответствующие полностью взаимозаменяемым товарам, т. е. ситуации, когда уменьшение
- 32. Задание на самостоятельную подготовку Найти и проанализировать другие виды функций полезности. Функцию полезности с полным дополнением
- 33. Общая постановка задачи состоит в поиске набора (х,y) максимизирующего функцию полезности и не превосходящего при этом
- 34. Задача минимизации стоимости. Общая постановка задачи состоит в поиске набора (X,Y) минимальной стоимости, обеспечивающего заданную полезность
- 35. Нахождение функций спроса. Определение. Пусть функция полезности U(x,y) при любых положительных Р1, Р2 и I имеет
- 37. Скачать презентацию

































 Ренессанс и Реформация: в поисках новой личности.
Ренессанс и Реформация: в поисках новой личности. Как переписать приложение с нуля и не потерпеть фиаско
Как переписать приложение с нуля и не потерпеть фиаско Виды подстанций
Виды подстанций «Основные требования, предъявляемые к лицам, претендующим на должность адвоката»
«Основные требования, предъявляемые к лицам, претендующим на должность адвоката»  Актеры и роли
Актеры и роли Искусство иконописи Византии
Искусство иконописи Византии Презентация: Биография и научная деятельность
Презентация: Биография и научная деятельность  Святой праведный Иоанн Кронштадтский
Святой праведный Иоанн Кронштадтский Пространственные конструкции
Пространственные конструкции сновные принципы построения ЕСЭ РФ
сновные принципы построения ЕСЭ РФ Урок №32(113) Соотношение единиц длины (м, дм, см). Решение задач
Урок №32(113) Соотношение единиц длины (м, дм, см). Решение задач  Электрические двигатели приводов
Электрические двигатели приводов Презентация на тему "Роль и место Интернет-ресурсов в практической деятельности врачей и провизоров-фармацевтов" - скачать пр
Презентация на тему "Роль и место Интернет-ресурсов в практической деятельности врачей и провизоров-фармацевтов" - скачать пр Заключительный этап Всероссийской олимпиады профессионального мастерства. Ветеринария и зоотехния
Заключительный этап Всероссийской олимпиады профессионального мастерства. Ветеринария и зоотехния Samsung Training Manual For LED TV ES7000 Series
Samsung Training Manual For LED TV ES7000 Series S&P 500
S&P 500 Разработка многопотоковых программ
Разработка многопотоковых программ  SH-SL «Second Hands – Second Life»
SH-SL «Second Hands – Second Life» Презентация на тему "Фотоальбом Павлиської школи імені Василя Сухомлинського" - скачать презентации по Педагогике
Презентация на тему "Фотоальбом Павлиської школи імені Василя Сухомлинського" - скачать презентации по Педагогике Рельсо-балоный цех АО ЕВРАЗ НТМК. Прохождение практики
Рельсо-балоный цех АО ЕВРАЗ НТМК. Прохождение практики Толкование уголовного закона
Толкование уголовного закона Урок алгебры в 9 классе Тема: «Решение неравенств методом интервалов» Выполнила: Ямалетдинова А. Н. МОУ «Аминевская СОШ»
Урок алгебры в 9 классе Тема: «Решение неравенств методом интервалов» Выполнила: Ямалетдинова А. Н. МОУ «Аминевская СОШ» «Показатели, характеризующие участие отдельной страны в международном разделении труда» Подготовила студентка экономического ф
«Показатели, характеризующие участие отдельной страны в международном разделении труда» Подготовила студентка экономического ф Некоторые особенности преаналитического этапа измерения концентрации каталитической активности ферментов Т.И.Лукичёва, В.В.М
Некоторые особенности преаналитического этапа измерения концентрации каталитической активности ферментов Т.И.Лукичёва, В.В.М Нуклеофильное замещение у винильного атома углерода
Нуклеофильное замещение у винильного атома углерода
 Античная лингвистическая традиция
Античная лингвистическая традиция Мультимедийное оборудование в профессиональной деятельности
Мультимедийное оборудование в профессиональной деятельности Аналитическая юриспруденция
Аналитическая юриспруденция