Содержание
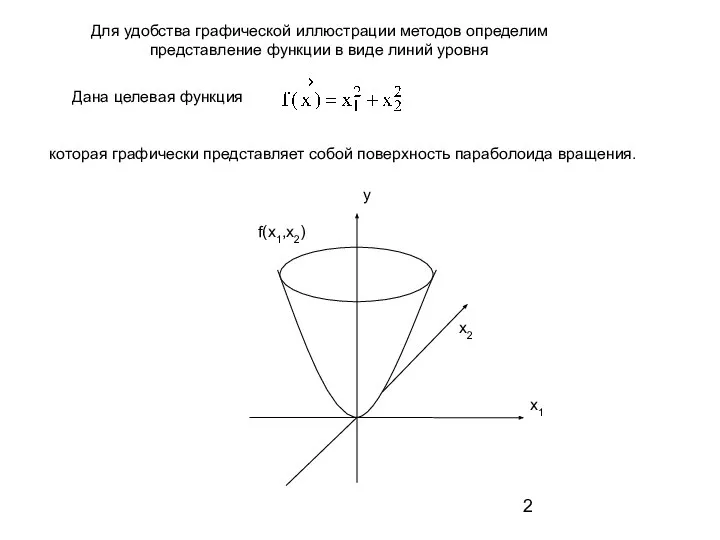
- 2. Для удобства графической иллюстрации методов определим представление функции в виде линий уровня Дана целевая функция которая
- 3. Проведем сечения поверхности равно отстоящими плоскостями, которые параллельны плоскости изменения переменных x1 и x2. Линии этих
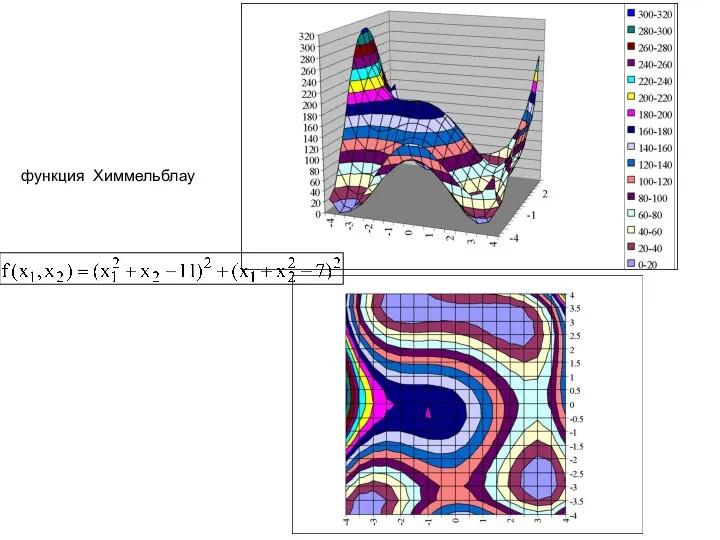
- 4. функция Химмельблау
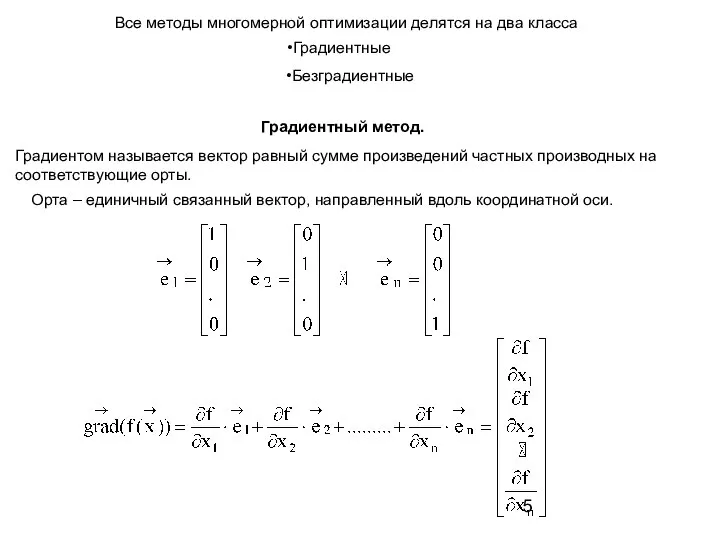
- 5. Все методы многомерной оптимизации делятся на два класса Градиентом называется вектор равный сумме произведений частных производных
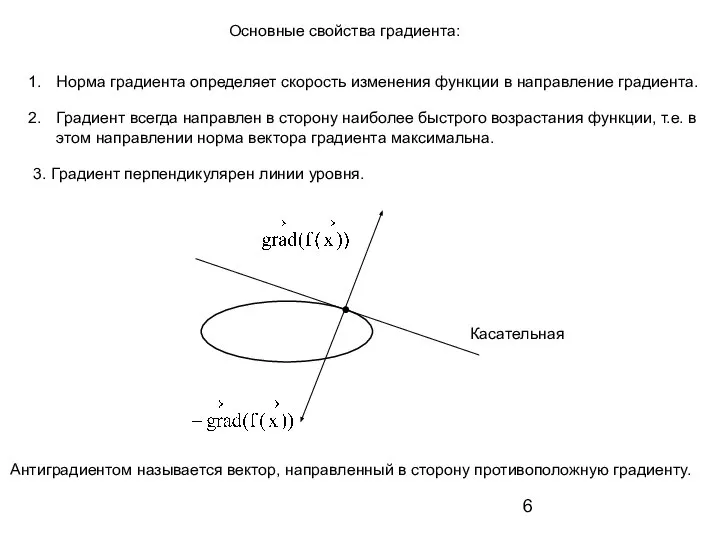
- 6. Норма градиента определяет скорость изменения функции в направление градиента. Градиент всегда направлен в сторону наиболее быстрого
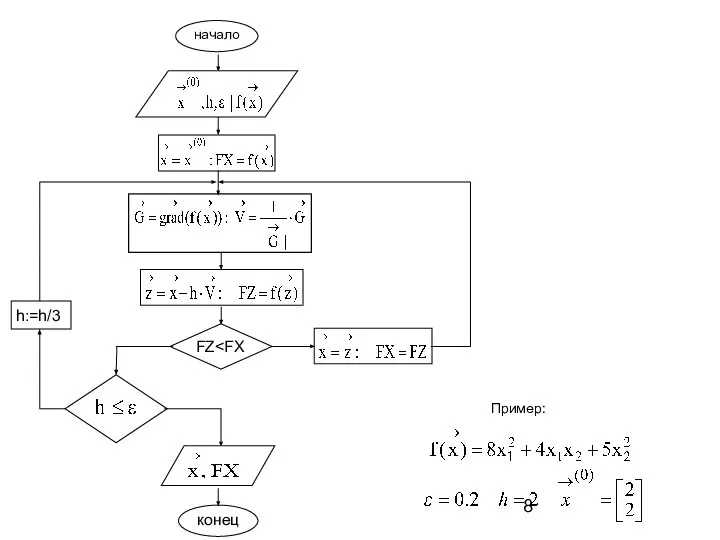
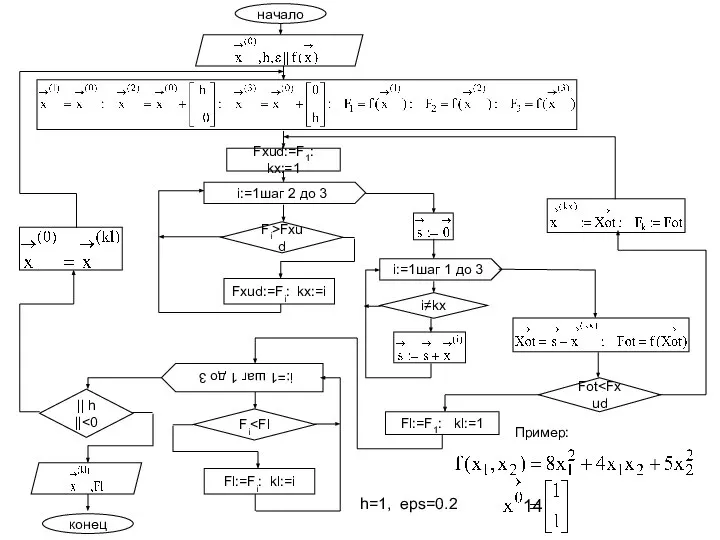
- 7. Алгоритм 1. Дана функция n переменных точность ε, параметр шага h, задаем начальное приближение вычисляем значение
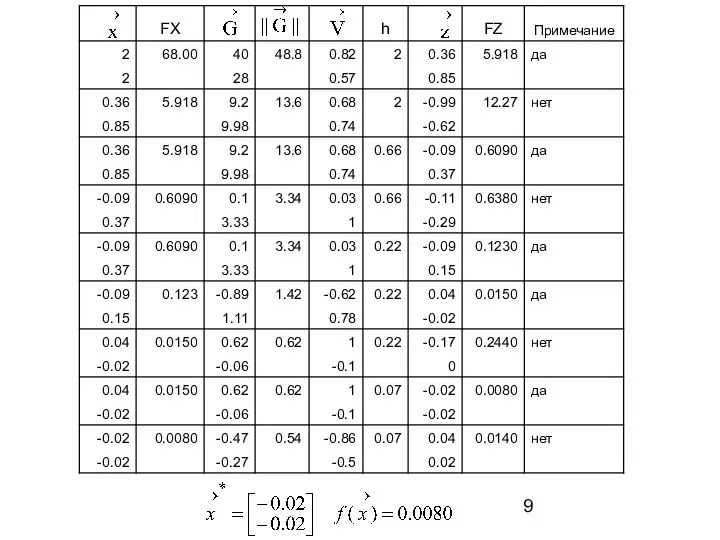
- 8. начало FZ h:=h/3 конец Пример:
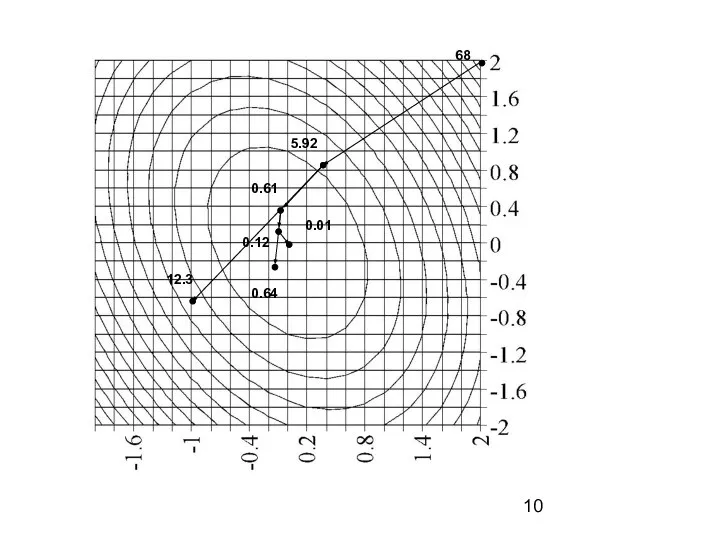
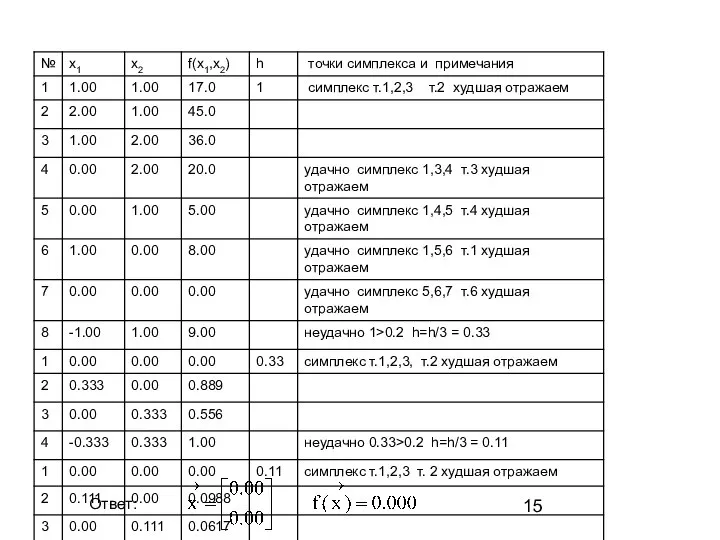
- 10. 68 5.92 12.3 0.61 0.64 0.12 0.01
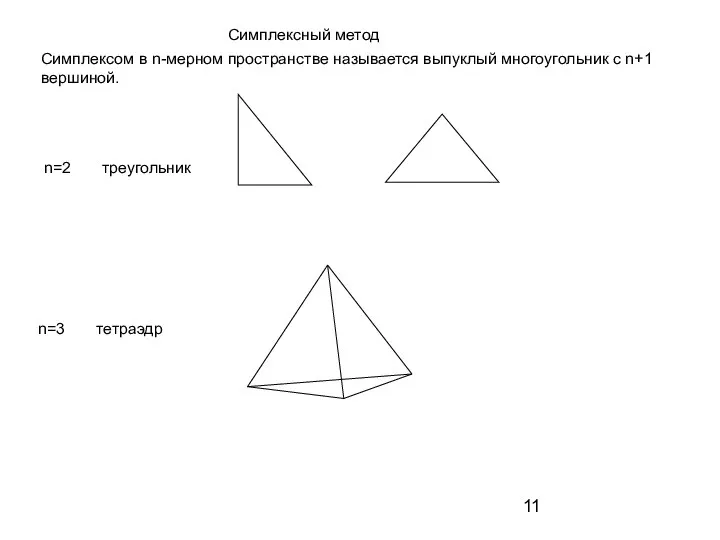
- 11. Симплексный метод Симплексом в n-мерном пространстве называется выпуклый многоугольник с n+1 вершиной. n=2 треугольник n=3 тетраэдр
- 12. Алгоритм 1. Дана функция 2x переменных точность ε, параметр h, начальное приближение 2. Вычисляем координаты вершин
- 13. 7. Условие не выполняется. Проверяем условие окончания h симплекса, уменьшаем длину грани h=h/3 и повторяем с
- 14. конец Fi>Fxud i:=1шаг 1 до 3 Fxud:=F1: kx:=1 Fxud:=Fi: kx:=i i:=1шаг 2 до 3 i≠kx Fot
- 15. Ответ:
- 17. Скачать презентацию




 Теневая экономика в современных условиях. Выполнила: Учащаяся экономического факультета Гринева Наталия группы Э091
Теневая экономика в современных условиях. Выполнила: Учащаяся экономического факультета Гринева Наталия группы Э091 Мехатронные системы в различных сферах производственной деятельности
Мехатронные системы в различных сферах производственной деятельности Методология исследований в менеджменте и маркетинге
Методология исследований в менеджменте и маркетинге Презентация "Теория спроса и предложения. Равновесие на рынке" - скачать презентации по Экономике
Презентация "Теория спроса и предложения. Равновесие на рынке" - скачать презентации по Экономике Молодежное открытое правительство
Молодежное открытое правительство 79842
79842 Мотивация учения и ее формирование у учащихся начальной школы. ДЕНИСОВА В.А.
Мотивация учения и ее формирование у учащихся начальной школы. ДЕНИСОВА В.А.  Башкиры. Народы Поволжья
Башкиры. Народы Поволжья Программирование на языке ассемблер
Программирование на языке ассемблер Масленица
Масленица Диагностика систем управления
Диагностика систем управления Великий Леонардо да Винчи
Великий Леонардо да Винчи Оперативный ток
Оперативный ток Проектирование здания учебно-тренажерного комплекса Саратовского подразделения Приволжского УЦПК
Проектирование здания учебно-тренажерного комплекса Саратовского подразделения Приволжского УЦПК Оценка сложности алгоритмов
Оценка сложности алгоритмов Презентация Товары к которым применяются запреты или ограничения на ввоз или вывоз
Презентация Товары к которым применяются запреты или ограничения на ввоз или вывоз Нуклеофильное замещение у винильного атома углерода
Нуклеофильное замещение у винильного атома углерода
 СТУПЕНЬКИ К ШКОЛЕ ПСИХОЛОГО-ПЕДАГОГИЧЕСКАЯ ГОТОВНОСТЬ РЕБЕНКА К ШКОЛЕ
СТУПЕНЬКИ К ШКОЛЕ ПСИХОЛОГО-ПЕДАГОГИЧЕСКАЯ ГОТОВНОСТЬ РЕБЕНКА К ШКОЛЕ Новый год в Китае
Новый год в Китае Диаграмма классов UML. The Unified Modeling Language
Диаграмма классов UML. The Unified Modeling Language Организация и проведение криминологического исследования
Организация и проведение криминологического исследования Обычаи, обряды и традиции русского народа
Обычаи, обряды и традиции русского народа Есептеуіш жүйенің даму тарихы
Есептеуіш жүйенің даму тарихы Қылмыстық кодекс
Қылмыстық кодекс Вина во Франции
Вина во Франции  Мезенская роспись - презентация_
Мезенская роспись - презентация_ Презентация Основы таможенного дела
Презентация Основы таможенного дела Никола́й Ива́нович Лобаче́вский (1793-1856) - русский математик, создатель неевклидовой геометрии
Никола́й Ива́нович Лобаче́вский (1793-1856) - русский математик, создатель неевклидовой геометрии