Содержание
- 2. Метод деления на три равных отрезка. Дан отрезок [a;b] на котором определена функция f(x) и точность
- 5. Попробуем увеличить долю сокращения отрезка Дан отрезок [a;b] на котором определена функция f(x) и точность ε.
- 8. Попробуем разбивать отрезок на такие части, чтобы одну из двух точек и соответствующее значение функции мы
- 9. Метод Золотого сечения. Дан отрезок [a;b] на котором определена функция f(x) и точность ε. Надо уточнить
- 10. начало F2 x, f(x) a, b, ε || f(x). x1 := a; x4:=b: Z=(3-√5)/2 x2:=x1+Z(x4-x1); x3:=x4-Z(x4-x1)
- 12. Скачать презентацию
Метод деления на три равных отрезка.
Дан отрезок [a;b] на котором определена
Метод деления на три равных отрезка.
Дан отрезок [a;b] на котором определена
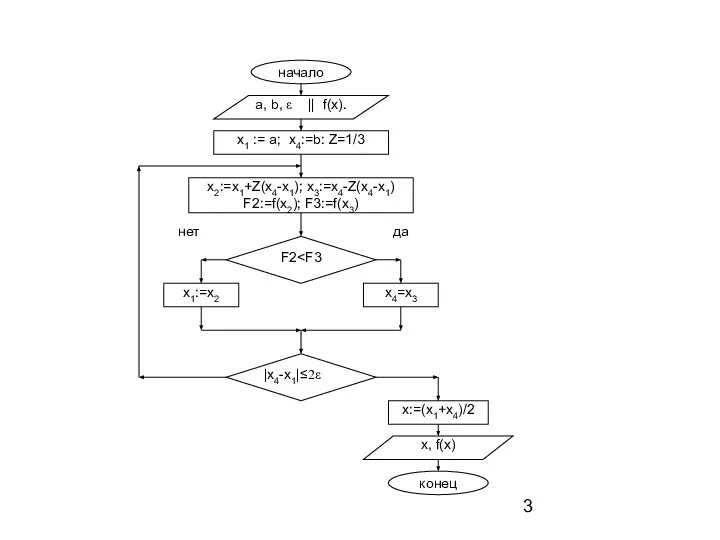
Делим отрезок на три равные части и определяем точку x2=x1+Z(x4-x1) и точку x3=x4-Z(x4-x1). Вычисляем значения функции в этих точках F2=f(x2) F3=f(x3).
Определяем новый отрезок, содержащий точку экстремума, сравнив значения функций F2 и F3. Если F2 < F3, то границы нового отрезка определим как x1=x1, а x4=x3, иначе x1=x2, а x4=x4.
Проверяем условие окончания итерационного процесса | x4-x1 | ≤ 2ε. Если оно выполняется, то определим решение, как x=(x4+x1)/2 и значение функции в этой точке f(x). Иначе перейдем на пункт 2.
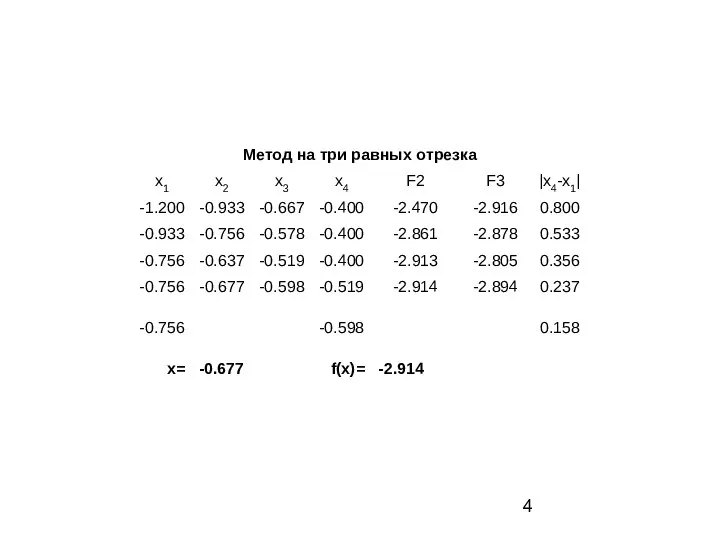
Введем понятие эффективности, как отношение доли сокращения отрезка к количеству вычисления функции на одной итерации тогда Q=0,33/2≈0,17
Попробуем увеличить долю сокращения отрезка
Дан отрезок [a;b] на котором определена функция
Попробуем увеличить долю сокращения отрезка
Дан отрезок [a;b] на котором определена функция
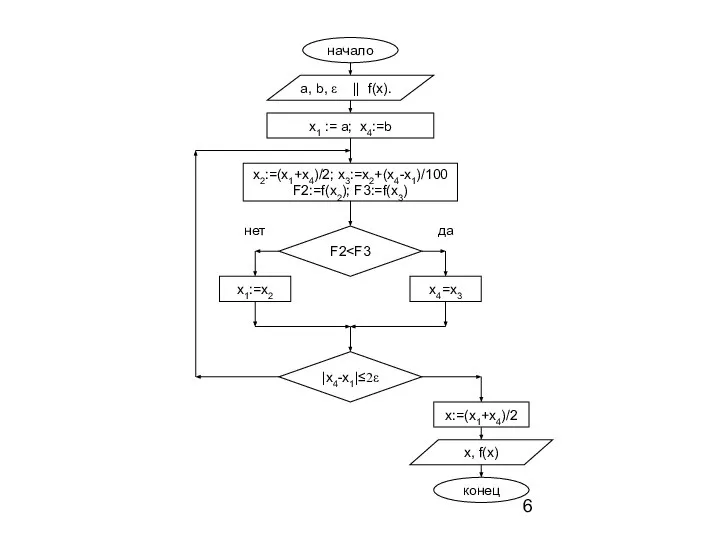
Делим отрезок пополам и определяем точку середины x2=(x4+x1)/2 и точку x3, отстоящую на незначительное расстояние от середины x3=x2+(x4-x1)/100. Вычисляем значения функции в этих точках F2=f(x2) F3=f(x3).
Определяем новый отрезок, содержащий точку экстремума, сравнив значения функций F2 и F3. Если F2 < F3, то границы нового отрезка определим как x1=x1, а x4=x3, иначе x1=x2, а x4=x4.
Проверяем условие окончания итерационного процесса | x4-x1 | ≤ 2ε. Если оно выполняется, то определим решение, как x=(x4+x1)/2 и значение функции в этой точке f(x). Иначе перейдем на пункт 2.
Метод деления отрезка пополам.
Эффективность метода Q≈0,5/2=0,25
Попробуем разбивать отрезок на такие части, чтобы одну из двух точек
Попробуем разбивать отрезок на такие части, чтобы одну из двух точек
делим на
Заменяем
Решая получим
Метод Золотого сечения.
Дан отрезок [a;b] на котором определена функция f(x) и
Метод Золотого сечения.
Дан отрезок [a;b] на котором определена функция f(x) и
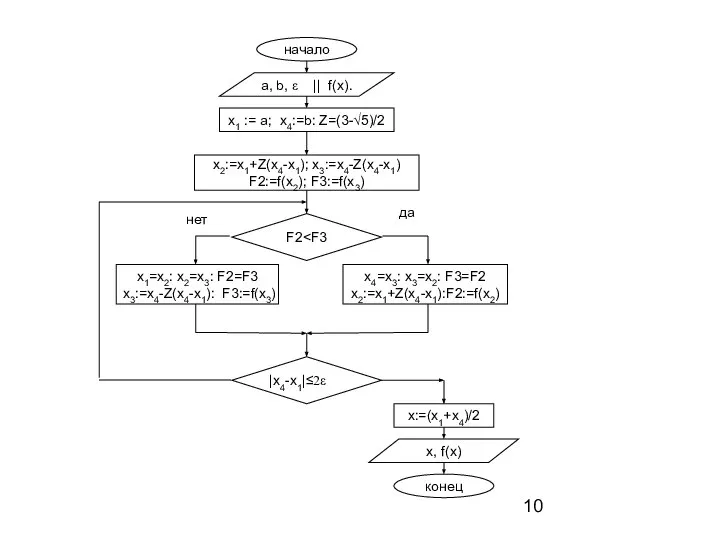
Делим отрезок на три части и определяем точку x2=x1+Z(x4-x1) и точку x3=x4-Z(x4-x1). Вычисляем значения функции в этих точках F2=f(x2) F3=f(x3).
Определяем новый отрезок, содержащий точку экстремума, сравнив значения функций F2 и F3. Если F2 < F3, то границы нового отрезка определим как x1=x1, x4=x3 , x3=x2, F3=F2 x2=x1+z(x4-x1) F2=f(x2) иначе x1=x2, x4=x4, x2=x3 F2=F3 x3=x4-z(x4-x1) F3= f(x3).
Проверяем условие окончания итерационного процесса | x4-x1 | ≤ 2ε. Если оно выполняется, то определим решение, как x=(x4+x1)/2 и значение функции в этой точке f(x). Иначе перейдем на пункт 3.
Введем понятие эффективности, как отношение доли сокращения отрезка к количеству вычисления функции на одной итерации тогда Q=0,3819/1≈0,3819
начало
F2x, f(x)
a, b, ε || f(x).
x1 := a; x4:=b: Z=(3-√5)/2
x2:=x1+Z(x4-x1); x3:=x4-Z(x4-x1)
F2:=f(x2);
начало
F2 x, f(x) a, b, ε || f(x). x1 := a; x4:=b: Z=(3-√5)/2 x2:=x1+Z(x4-x1); x3:=x4-Z(x4-x1)
F2:=f(x2);
|x4-x1|≤2ε
конец
x:=(x1+x4)/2
нет
да
x1=x2: x2=x3: F2=F3
x3:=x4-Z(x4-x1): F3:=f(x3)
x4=x3: x3=x2: F3=F2
x2:=x1+Z(x4-x1):F2:=f(x2)
![Метод деления на три равных отрезка. Дан отрезок [a;b] на котором](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1297922/slide-1.jpg)
![Попробуем увеличить долю сокращения отрезка Дан отрезок [a;b] на котором определена](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1297922/slide-4.jpg)


![Метод Золотого сечения. Дан отрезок [a;b] на котором определена функция f(x)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1297922/slide-8.jpg)
 Археологические находки-свидетели истории
Археологические находки-свидетели истории Социальные изменения и социальные процессы. Прогресс и регресс.
Социальные изменения и социальные процессы. Прогресс и регресс. Пермский край. Город Чайковский
Пермский край. Город Чайковский Основы алгоритмизации и программирования. Понятие и свойства алгоритма
Основы алгоритмизации и программирования. Понятие и свойства алгоритма Камерный ансамбль Allegro
Камерный ансамбль Allegro На рубеже XIX-XX веков демократия в странах Запада
На рубеже XIX-XX веков демократия в странах Запада Основные термины и определения, используемые при подтверждении, оценке и убеждении в соответствии (ISO 17000
Основные термины и определения, используемые при подтверждении, оценке и убеждении в соответствии (ISO 17000 Программирование на языке C++
Программирование на языке C++ Презентация "на тему «Личность и поведение в организации»" - скачать презентации по Экономике
Презентация "на тему «Личность и поведение в организации»" - скачать презентации по Экономике Футбол в Україні
Футбол в Україні Художники XVIII века Кого называли художниками–портретистами? Почему некоторые картины были подписаны так: «Неизвестный автор. XVIII
Художники XVIII века Кого называли художниками–портретистами? Почему некоторые картины были подписаны так: «Неизвестный автор. XVIII Принципы физического воспитания
Принципы физического воспитания Отток клиентов от Дом.ru
Отток клиентов от Дом.ru Классификация колебаний
Классификация колебаний  Задание на проектирование пешеходной зоны в исторической части города Ростов-на-Дону
Задание на проектирование пешеходной зоны в исторической части города Ростов-на-Дону Молекулярные перегруппировки
Молекулярные перегруппировки  Моисей и Исход. Исход Израиля из Египта и вхождение в Ханаан
Моисей и Исход. Исход Израиля из Египта и вхождение в Ханаан Типы данных и объявление переменных
Типы данных и объявление переменных Операторы ввода и вывода в Pascal
Операторы ввода и вывода в Pascal Проверочная работа № 1 «Стили архитектуры»
Проверочная работа № 1 «Стили архитектуры» функции по защите информации структурных подразделений предприятия и их руководителей
функции по защите информации структурных подразделений предприятия и их руководителей Презентация на тему "Оптимизация управления взаимодействием детского сада и семьи, через использование информационно – коммун
Презентация на тему "Оптимизация управления взаимодействием детского сада и семьи, через использование информационно – коммун Новый год. История и традиции
Новый год. История и традиции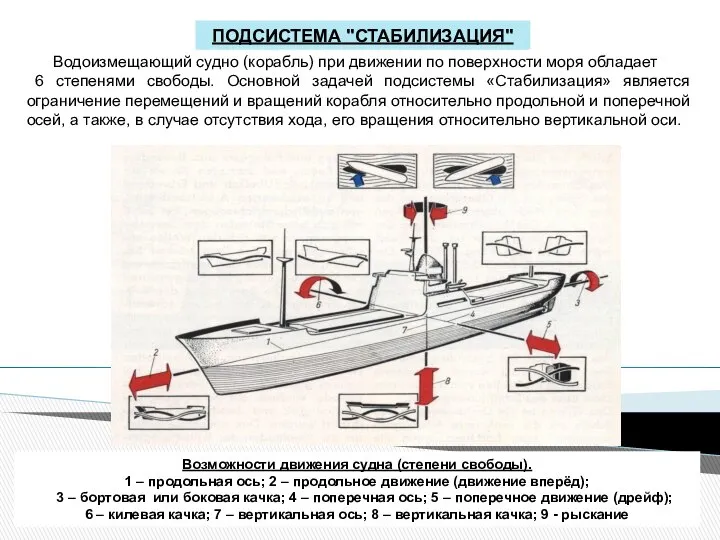 Подсистема «Стабилизация»
Подсистема «Стабилизация» ПУСТЫНИ Показ подготовлен ученицей 4«Б» класса ГОУСОШ №2031 Сафоновой Ольгой учитель: Попель Татьяна Ивано
ПУСТЫНИ Показ подготовлен ученицей 4«Б» класса ГОУСОШ №2031 Сафоновой Ольгой учитель: Попель Татьяна Ивано Модернизация горелочных устройств котлоагрегата КВГМ-100
Модернизация горелочных устройств котлоагрегата КВГМ-100 Презентация Анализ внешней торговли товарами и услугами Южной Кореи и Тайваня
Презентация Анализ внешней торговли товарами и услугами Южной Кореи и Тайваня  Культура и ценности
Культура и ценности