Содержание
- 2. Методы оптимизации Говоря о задачах минимизации выделяют несколько общих моментов: Определяют некоторую «скалярную» меру качества –
- 3. Методы спуска Продолжим рассмотрение итерационных методов, являющиеся более изощренными по сравнению с методами нулевого порядка. Формулируются
- 4. Методы спуска Методами спуска называются методы рассмотренного выше типа, в которых векторы являются векторами спуска. Поскольку
- 5. Методы спуска Различные способы выбора направлений спуска приводят к разным методам минимизации: Метод Ньютона, в котором
- 6. Методы спуска Градиентный метод или метод скорейшего спуска, соответствующий выбору направления спуска по формуле . Таким
- 7. Выбор направления недостаточен для полного задания метода спуска. Ведь остается еще проблема определения так, чтобы шаг
- 8. К сожалению, за исключением редких случаев, точное решение задачи одномерной минимизации невозможно, поскольку задача нелинейна. Одна
- 9. Линейный поиск Методика линейного поиска Рассмотрим итеративные методы, останавливающиеся при выполнении некоторого критерия останова итеративного процесса.
- 10. Однако простейшая процедура, заключающаяся в выборе достаточно большого начального значения , которое затем уменьшается (делением пополам)
- 11. Это требование обеспечивает некую усредненную скорость спуска на очередной итерации не меньше определенной доли от величины,
- 12. Свойство. Предположим, что для всех . Тогда существует интервал такой, что в методе спуска условия (*)
- 13. Линейный поиск
- 14. http://www.hbmeyer.de/backtrack/backtren.htm Поиск с возвратом (англ. Backtracking) — общий метод нахождения решений задачи, в которой требуется полный
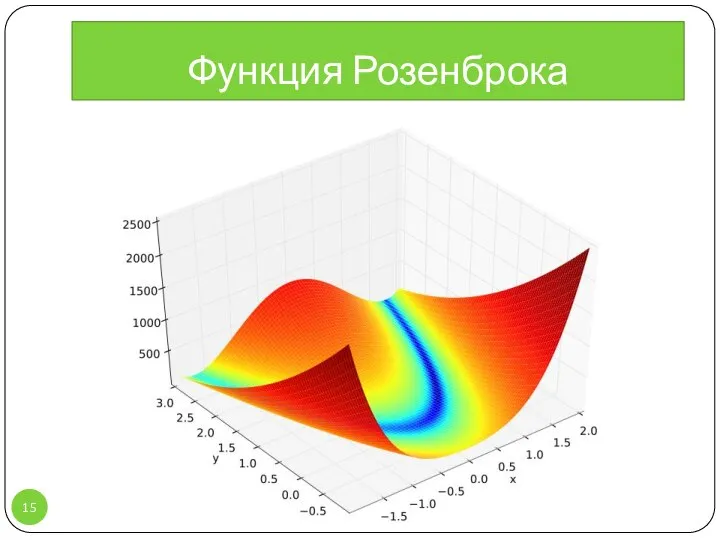
- 15. Функция Розенброка
- 17. Скачать презентацию













 Презентация "КРАСАУСКАС СТАСИС АЛЬГИРДО" - скачать презентации по МХК
Презентация "КРАСАУСКАС СТАСИС АЛЬГИРДО" - скачать презентации по МХК CSS. Группировка. Идентификаторы. Классы. Псевдоклассы и псевдоэлементы
CSS. Группировка. Идентификаторы. Классы. Псевдоклассы и псевдоэлементы Организация мероприятий строительного контроля
Организация мероприятий строительного контроля Диуретики
Диуретики Тема3_Рыночный механизм 2019
Тема3_Рыночный механизм 2019 Культура и этнос. Роль культуры в этнической самоидентификации. Этническая культура и национальная культура
Культура и этнос. Роль культуры в этнической самоидентификации. Этническая культура и национальная культура Устное народное творчество. Русские народные загадки
Устное народное творчество. Русские народные загадки Нацизм. Прошлое и настоящее
Нацизм. Прошлое и настоящее Презентация Понятие и основные характеристики групп. Классификация групп
Презентация Понятие и основные характеристики групп. Классификация групп  Образ Петра I в произведениях искусства Материалы к урокам по истории России, МХК, литературы
Образ Петра I в произведениях искусства Материалы к урокам по истории России, МХК, литературы Преобразования типов. Лекция 4
Преобразования типов. Лекция 4 Презентация на тему "Мышцы кисти" - скачать презентации по Медицине
Презентация на тему "Мышцы кисти" - скачать презентации по Медицине Презентация опыта работы Шумилова Анжелика Владимировна воспитатель Муниципальное бюджетное дошкольное образовательное учреж
Презентация опыта работы Шумилова Анжелика Владимировна воспитатель Муниципальное бюджетное дошкольное образовательное учреж Бионика. Влияние природы на развитие инженерии и архитектуры
Бионика. Влияние природы на развитие инженерии и архитектуры Ненаркотические анальгетики
Ненаркотические анальгетики Лицензирование деятельности в сфере НИОКР и ее особенности для оборонной отрасли
Лицензирование деятельности в сфере НИОКР и ее особенности для оборонной отрасли Interesting 1970 years
Interesting 1970 years Аттестационная работа. Организация проектной деятельности учащихся на уроках ОДНКНР
Аттестационная работа. Организация проектной деятельности учащихся на уроках ОДНКНР ГОУ ВПО «КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ИМ. ПРОФ. В.Ф.ВОЙНО-ЯСЕНЕЦКОГО ПО ЗДРАВООХРАНЕНИЮ И СОЦИАЛЬНОМУ
ГОУ ВПО «КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ ИМ. ПРОФ. В.Ф.ВОЙНО-ЯСЕНЕЦКОГО ПО ЗДРАВООХРАНЕНИЮ И СОЦИАЛЬНОМУ Рождество Христово
Рождество Христово Преступления против жизни. (Тема 21)
Преступления против жизни. (Тема 21) Примеры автоматизированного тестирования игр в Unity
Примеры автоматизированного тестирования игр в Unity Построение асимптотических ЛАЧХ
Построение асимптотических ЛАЧХ Тос «Весенний». Отчетная конференция за 2017 год
Тос «Весенний». Отчетная конференция за 2017 год ОГЭ. Немецкий язык
ОГЭ. Немецкий язык Автоматизация в современном производстве
Автоматизация в современном производстве устные вычисления (3) - презентация для начальной школы
устные вычисления (3) - презентация для начальной школы Урок по теме «Народные праздники древних славян» 3 класс (Программа «Начальная школа XXI века»)
Урок по теме «Народные праздники древних славян» 3 класс (Программа «Начальная школа XXI века»)