Содержание
- 2. 2.1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ В некоторых случаях ограничения в задаче оптимизации позволяют через один из параметров оптимизации
- 3. Если функция f(x) не имеет на множестве D(f) наименьшего значения, то (2.1) следует заменить формулировкой задачи
- 4. Функцию f(x) называют унимодальной функцией на отрезке [а, b], если существует такая точка x* ∈ [a,
- 5. Область определения D(f) минимизируемой функции f(x) может состоять из нескольких промежутков, не имеющих граничных точек. В
- 6. 2.2. ПАССИВНЫЙ И ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК Пусть требуется найти наименьшее значение или точную нижнюю грань f* скалярной
- 7. Для методов пассивного поиска алгоритм выбора точек xk, k = 1, 2, …, N, — это
- 8. Значение lN(P) представляет собой оценку сверху погрешности вычисления точки соответствующей искомому значению f* произвольной функции которая
- 9. Пример 2.1. Рассмотрим один из возможных подходов к выделению из промежутка X в области определения D(f)
- 10. 2.3. ОПТИМАЛЬНЫЙ И ПАССИВНЫЙ ПОИСК Пусть требуется путем пассивного поиска найти точку x* ∈ [0, 1],
- 11. Если при N = 2 (рис. 2.5) две точки расположить на отрезке [0,1] так, чтобы они
- 12. Пример 2.2. При заданной наибольшей допустимой длине интервала неопределенности, используя оптимальный пассивный поиск, найдем точку ,
- 13. 2.4. МЕТОДЫ ПОСЛЕДОВАТЕЛЬНОГО ПОИСКА Метод дихотомии. Рассмотрим последовательный поиск точки x* ∈ [0, 1], в которой
- 14. Из этого равенства выводим следующую формулу длины lk отрезка [ак ,bк], получаемого на k-м шаге метода
- 15. Метод золотого сечения. Как известно, золотым сечением отрезка называют такое его деление на две неравные части,
- 16. Выясним, чему равно отношение золотого сечения. Так как точки xк1 и xk2, xк1 bk -xk2 =
- 17. Пусть на к-м шаге, к ≥ 2, последовательного поиска по методу золотого сечения выбран отрезок [аk,bk]
- 18. Метод Фибоначчи. Пусть при поиске точки x* ∈ [0, 1], в которой унимодальная на отрезке [0,
- 19. В такой ситуации при выборе = xn длина интервала неопределенности равна пока неизвестной длине ln отрезка
- 20. Все коэффициенты Fm принадлежат множеству натуральных чисел, и их называют числами Фибоначчи*. В табл. 2.1 представлены
- 21. При l1 = 1 из (2.15) находим l2= Fn/Fn+1. Таким образом, учитывая (2.13), заключаем, что на
- 23. Скачать презентацию
2.1. ПРЕДВАРИТЕЛЬНЫЕ
ЗАМЕЧАНИЯ
В некоторых случаях ограничения в задаче оптимизации позволяют
2.1. ПРЕДВАРИТЕЛЬНЫЕ
ЗАМЕЧАНИЯ
В некоторых случаях ограничения в задаче оптимизации позволяют
f(x) → min, x ∈ D(f) ⊂ R, (2.1)
поиска наименьшего значения f = f(x*) функции f(x) и точки x* ∈ D(f), в которой f(x) принимает это значение. Для краткости будем говорить об одномерной минимизации, имея в виду нахождение наименьшего значения функции f(x) на множестве D(f) и точек, в которых это значение достигается.
Изучение методов одномерной минимизации важно не только для решения задачи (2.1), имеющей самостоятельное значение. Эти методы являются также существенной составной частью методов многомерной минимизации, при помощи которых находят наименьшее значение действительных функций многих переменных.
Пусть область определения D(f) функции f(x) есть промежуток числовой прямой. Напомним, что если D(f) — отрезок и f(x) непрерывна на нем, то она имеет на этом отрезке наименьшее значение. Но при наличии на отрезке точек разрыва функции она может не иметь на нем наименьшего значения. Оно может не существовать и в том случае, когда D(f) является интервалом или полуинтервалом.
Если функция f(x) не имеет на множестве D(f) наименьшего значения,
Если функция f(x) не имеет на множестве D(f) наименьшего значения,
(2.2)
Тогда под решением задачи минимизации такой функции на D(f) следует понимать построение последовательности {хп} точек из D(f), для которой существует предел
(2.3)
и нахождение этого предела. Если функция f(x) достигает на множестве D(f) своего наименьшего значения
Например, функция f(x) = 1/ х на множестве D(f) = [1, 2) не достигает наименьшего значения, хотя и ограничена снизу. Точная нижняя грань функции в данном случае равна 1/2. В качестве последовательности {хп} точек в полуинтервале [1. 2), для которой справедливо (2.3), можно выбрать {2 - 1/n}. Тогда
и последовательность {f(xn)} сходится к числу
Функция может достигать наименьшего значения как в единственной точке, так и на некотором множестве точек, конечном, счетном или несчетном. Например, функция f(x) = x4 определена на всей числовой прямой и достигает своего наименьшего значения в единственной точке которая является ее точкой минимума. Функция f(x) = х4 — 2х2 + 2 также определена на всей числовой прямой и достигает наименьшего значения в точках Функция f(x)=cosx достигает наименьшего значения на счетном множестве а а функция f(x) = |x + 1| + |x — 1| — на несчетном множестве
Функцию f(x) называют унимодальной функцией на отрезке [а, b], если
Функцию f(x) называют унимодальной функцией на отрезке [а, b], если
Точка x* может быть внутренней точкой отрезка [а, b] (т.е. a < x* < b, см. рис. а-г) или совпадать с одним из его концов (x* = a или x* = b, см. рис. д,е). Унимодальная функция не обязательно непрерывна на отрезке [а, b] (см. рис. в, г).
Функцию f(x), достигающую на отрезке [а, b] наименьшего значения в единственной точке x* ∈ [a, b], убывающую при x ∈ [a, x*] и возрастающую при x ∈ [x*, b], будем называть строго унимодальной на отрезке [а, b] (на рисунке строго унимодальными являются все функции, кроме функции на рис. г).
Область определения D(f) минимизируемой функции f(x) может состоять из нескольких
Область определения D(f) минимизируемой функции f(x) может состоять из нескольких
Если функция дифференцируема в промежутке, то возможно использование необходимого и достаточного условий локального минимума [II]. Однако в прикладных задачах нередки ситуации, когда трудно вычислить производные функции (например, если функция не задана в аналитическом виде). Более того, не исключено, что значения функции известны или могут быть вычислены только в отдельных точках. В таких ситуациях использование необходимого и достаточного условий локального минимума невозможно и следует применять другие методы решения задачи оптимизации. Методы минимизации функции одного переменного, в которых используют значения функции в точках рассматриваемого промежутка и не используют значения ее производных, называют методами прямого поиска.
2.2. ПАССИВНЫЙ И ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК
Пусть требуется найти наименьшее значение или
2.2. ПАССИВНЫЙ И ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК
Пусть требуется найти наименьшее значение или
1) все N точек xk, k = 1, 2, …, N, в которых будут вычислены значения функции, выбирают заранее (до вычисления функции в этих точках);
2) точки xk выбирают последовательно (для выбора последующей точки используют значения функции, вычисленные в предыдущих точках).
В первом случае поиск значения f* называют пассивным, а во втором — последовательным. Естественно ожидать, что последовательный поиск лучше пассивного. В этом можно убедиться, вспомнив детскую игру, в которой надо найти спрятанную вещь, задавая вопросы и получая на них ответы „да” или „нет". Задавая вопросы последовательно с учетом предыдущих ответов, можно найти спрятанную вещь за меньшее число вопросов (итераций), чем, задав определенное количество заранее подготовленных вопросов сразу.
Так как в прикладных задачах вычисление каждого значения функции может быть достаточно трудоемким, то целесообразно выбрать такую стратегию поиска, чтобы значение f* с заданной точностью было найдено наиболее экономным путем. Будем считать, что стратегия поиска определена, если:
определен алгоритм выбора точек xk, k = 1, 2, …, N;
определено условие прекращения поиска, т.е. условие, при выполнении которого значение f* считают найденным с заданной точностью.
Для методов пассивного поиска алгоритм выбора точек xk, k =
Для методов пассивного поиска алгоритм выбора точек xk, k =
В методах последовательного поиска количество точек xk обычно не задают заранее. Однако объективное сравнение различных методов прямого поиска нужно проводить при одинаковом количестве n вычисленных значений функции f(x). После п вычислений обычно указывают интервал (или отрезок) длины ln, называемый интервалом неопределенности, в котором гарантированно находится точка x*, соответствующая значению f*. Условие прекращения вычислений в случае пассивного или последовательного поиска примем одинаковым — выполнение неравенства ln ≤ ε*, где ε* — заданная наибольшая допустимая длина интервала неопределенности.
Длина lп зависит как от самого метода прямого поиска Р, так и от минимизируемой функции f(x), т.е. ln=ln(P,f). Зависимость lп от п дает оценку скорости сходимости конкретного метода прямого поиска Р к искомому значению заданной функции f(x). Различные методы из некоторого множества методов прямого поиска сравнивают обычно при выбранном фиксированном значении п=N на некотором достаточно широком классе функций. В качестве такого класса можно выбрать множество унимодальных функций, определенных на фиксированном отрезке Для метода прямого поиска примем наихудшую оценку
Если „наихудшей” унимодальной функции не найдется, то оценку принимаем в виде
Значение lN(P) представляет собой оценку сверху погрешности вычисления точки соответствующей
Значение lN(P) представляет собой оценку сверху погрешности вычисления точки соответствующей
Этот критерий сравнения методов поиска определяет минимаксный метод поиска. Такой метод является наилучшим для всего множества унимодальных функций на отрезке в том смысле, что он дает наименьшую погрешность вычисления точки x*, соответствующей значению любой из рассматриваемых функций . Хотя вполне возможно, что существует некоторый конкретный метод, который для определенной специально подобранной унимодальной функции из множества обеспечит еще меньшую погрешность.
Все методы прямого поиска можно строить и сравнивать между собой на отрезке X = [0, 1]. Полученные результаты при необходимости нетрудно перенести на случай произвольного отрезка [а, b], так как любую точку отрезка [0,1] можно перевести в соответствующую ей точку отрезка [а, b] растяжением в b - а раз и сдвигом на а.
Если минимизируемая функция f(x) не является унимодальной на отрезке [а,b] (такую функцию называют мулътимодальной функцией на этом отрезке), то, даже если она непрерывна на [а, b], при поиске наименьшего значения f* функции на отрезке может возникнуть ошибка: будет найдена точка локального минимума, в которой значение функции не f*, а другое, большее. Чтобы избежать такой ошибки, в процесс минимизации включают предварительный этап, на котором отрезок минимизации разделяют на несколько отрезков, на каждом из которых минимизируемая функция унимодальна. Сравнительный анализ наименьших значений функции на этих отрезках позволяет найти искомое наименьшее значение f* на всем отрезке минимизации.
Пример 2.1. Рассмотрим один из возможных подходов к выделению из промежутка
Пример 2.1. Рассмотрим один из возможных подходов к выделению из промежутка
Может оказаться, что Тогда за искомый отрезок [а, b] можно сразу принять отрезок [х0, х1]. Но можно продолжить вычисления и, используя последовательный поиск, определять значения f(xk) в точках до тех пор, пока не будет выполнено неравенство Тогда следует принять [а, b] = [x0, xk-1] (на рис. 2.2 [а, b] = [x0, x2], поскольку точка x* должна быть либо на отрезке [x0, x3], либо на отрезке [x3, x2]). Надо сказать, что при этом можно „не заметить” по крайней мере, еще один отрезок, на котором функция унимодальна (штриховая линия на рис. 2.2).
Если , то используя последовательный поиск, вычисляем значения , где пока не будет выполнено неравенство что позволяет принять (на рис. 2.3 так как точка x* должна быть либо на отрезке либо на отрезке )
Отметим, что описанный подход не гарантирует нахождения отрезка унимодальности функции. Например, на рис. 2.3 штриховой линией показан график функции, для которой этот подход не позволяет обнаружить искомый отрезок.
2.3. ОПТИМАЛЬНЫЙ И ПАССИВНЫЙ ПОИСК
Пусть требуется путем пассивного поиска найти
2.3. ОПТИМАЛЬНЫЙ И ПАССИВНЫЙ ПОИСК
Пусть требуется путем пассивного поиска найти
Если N = 1, то единственную точку целесообразно выбрать в середине отрезка, т.е. принять х1 = 1/2 (рис. 2.4). В этом случае вследствие унимодальности функции f(x) имеем f* ≤ f(1/2). Поэтому наименьшая возможная длина интервала неопределенности равна l1* = 1 и можно гарантировать, что выбор в качестве точки x* ∈ [0, 1] точки х1 = 1/2 приведет к погрешности не более Δ1* = l1*/2 = 1/2. При любом ином положении точки х1 погрешность при выборе x* = x1 будет Δ1 ≥ Δ1*, так как в действительности точка x* может лежать на большей части отрезка [0, 1].
Если при N = 2 (рис. 2.5) две точки расположить
Если при N = 2 (рис. 2.5) две точки расположить
Рассуждая аналогично, можно заключить, что при N = 3 нужно также выбирать точки равномерно на отрезке [0,1]: x1 = 1/4, x2 = 2/4, x3 = 3/4, обеспечив точность нахождения точки и наименьшую длину интервала неопределенности. В случае произвольного по тем же соображениям надо выбирать точки
обеспечивая точность нахождения точки и наименьшую возможную длину
интервала неопределенности. Таким образом, оптимальный пассивный поиск состоит в выборе точек, равномерно расположенных на отрезке. При этом (2.5) дает оценку скорости сходимости пассивного поиска с ростом числа N точек, так как скорость сходимости любого метода прямого поиска можно характеризовать скоростью уменьшения интервала неопределенности с возрастанием N.
Пример 2.2. При заданной наибольшей допустимой длине интервала неопределенности, используя
Пример 2.2. При заданной наибольшей допустимой длине интервала неопределенности, используя
Из представленных результатов вычислений можно сделать вывод, что интервалом неопределенности является интервал (0,6, 0,8), а . Отметим, что при потребуется принять N = 199.
Рассуждения, проведенные выше, попутно обосновывают процедуру исключения отрезка, которую используют во всех методах прямого поиска точки минимума унимодальной функции одного переменного. Эта процедура состоит в следующем. Пусть на отрезке [а, b] числовой прямой расположены две точки с и d, а < с < d < b, и известны (или вычислены) значения f(с) и f(d) унимодальной на [а, b] функции f(x). Если f(с) < f(d) (рис. 2.6, а), то в силу унимодальности функции f(x) имеем x* ∈ [a, d], a отрезок [d, b] можно исключить из дальнейшего рассмотрения. Наоборот, если f(с) ≥ f(d) (рис. 2.6, б), то x* ∈ [c, b], а отрезок [а, с] далее можно не рассматривать.
Таким образом, в результате применения процедуры исключения отрезка получаем новый отрезок, вложенный в рассматриваемый и заведомо содержащий искомую точку . В методах пассивного поиска применение этой процедуры позволяет оценить наибольшую возможную погрешность нахождения точки . Все рассмотренные далее методы последовательного поиска используют процедуру исключения отрезка для выбора нового отрезка на каждом очередном шаге такого поиска.
2.4. МЕТОДЫ ПОСЛЕДОВАТЕЛЬНОГО ПОИСКА
Метод дихотомии. Рассмотрим последовательный поиск точки x*
2.4. МЕТОДЫ ПОСЛЕДОВАТЕЛЬНОГО ПОИСКА
Метод дихотомии. Рассмотрим последовательный поиск точки x*
Пусть известно, что на k-м шаге последовательного поиска (на первом шаге при k = 1 имеем а1 = 0 и b1= 1). На отрезке [аk, bk] длиной lк выберем две точки xk1= (ak + bk)/2 - δ и xк2= (ak + bk)/2 + δ (рис. 2.7), где δ > 0 — некоторое достаточно малое число. Вычислим значения f(xk1) и f(xk2) функции f(x) в этих точках и выполним процедуру исключения отрезка. В результате получим новый отрезок . Если длина lk+1 нового отрезка больше заданной наибольшей допустимой длины интервала неопределенности, то алгоритм метода дихотомии переходит к (k + 1)-му шагу, повторяя все описанные для k-го шага действия. Если же , то вычисления прекращают и полагают .
Так как то
Из этого равенства выводим следующую формулу длины lk отрезка [ак
Из этого равенства выводим следующую формулу длины lk отрезка [ак
Из (2.6) следует, что , но при этом Поэтому выполнение неравенства , означающее достижение заданной точности нахождения точки возможно лишь при условии выбора . Кроме того, нужно учитывать неизбежную погрешность, возникающую при вычислении приближенных значений функции f(x). Это приводит к дополнительной погрешности при нахождении точки (см. 2.7). Поэтому выбор значения δ ограничен и снизу, т.е.
Если эти неравенства нарушаются, то знак разности может не совпадать со знаком разности , что приводит к ошибочному выполнению процедуры исключения отрезка.
Итак, метод дихотомии — это последовательное построение на каждом к-м шаге поиска точек и , симметричных относительно середины отрезка [ак, bк] длины lк. После выполнения k-го шага будет выделен отрезок [ак+1, bk+1] длины lк+1 и вычислено N = 2k значений функции. Используя формулу (2.6) для длины отрезка (интервала неопределенности) и полагая l1 = 1, получаем
Сравнивая (2.8) с (2.5), видим, что скорость сходимости метода дихотомии значительно выше скорости сходимости оптимального пассивного поиска.
Отметим, что после исключения отрезка на k-м шаге описанного алгоритма точки хк1 и хк2 принадлежат новому отрезку [ак+1, bk+1], причем одна из них является внутренней для этого отрезка. Но вычисленное в этой точке значение функции f(x) в методе дихотомии не используют для исключения отрезка на следующем шаге, а проводят вычисления в двух новых точках. Существуют методы последовательного поиска, в которых на каждом k-м шаге начиная с к = 2 вычисляют лишь одно новое значение функции в точке, принадлежащей отрезку [ак+1, bk+1]. Это значение вместе с уже вычисленным на предыдущем шаге значением функции во внутренней точке отрезка [ак,bк] используют при выполнении процедуры исключения отрезка на следующем шаге последовательного поиска.
Метод золотого сечения. Как известно, золотым сечением отрезка называют такое
Метод золотого сечения. Как известно, золотым сечением отрезка называют такое
Термин „золотое сечение” ввел Леонардо да Винчи. Золотое сечение широко применяли при композиционном построении многих произведении мирового искусства, в том числе в античной архитектуре и в эпоху Возрождения.
Рассмотрим к-й шаг последовательного поиска. Чтобы выполнить процедуру исключения отрезка на этом шаге, отрезок [ак, bk] необходимо двумя внутренними точками xк1, xk2 , xк1 < xk2, разделить на три части. Эти точки выберем симметрично относительно середины отрезка [ак, bk] (рис. 2,8) и так, чтобы каждая из них производила золотое сечение отрезка [ак, bk]. В этом случае отрезок [ак+1, bk+1] внутри будет содержать одну из точек xк1, xk2 (другая будет одним из концов отрезка), причем эта точка будет производить золотое сечение отрезка [ак+1, bk+1]. Это вытекает из равенства длин отрезков [ак, xk1] и [xк2, bk]. Таким образом, на (к + 1)-м шаге в одной из точек xк+1,1и xк+1,2. значение функции вычислять не нужно. При этом отношение lk/lk+1 длин отрезков сохраняется от шага к шагу, т.е.
Число r называют отношением золотого сечения.
Последовательный поиск, в котором на k-м шаге каждая из симметрично выбранных на отрезке [аk, bk] точек xк1, xk2 осуществляет золотое сечение этого отрезка, называют методом золотого сечения. В этом методе каждое исключение отрезка уменьшает оставшийся отрезок в r раз.
Выясним, чему равно отношение золотого сечения. Так как точки xк1
Выясним, чему равно отношение золотого сечения. Так как точки xк1
bk -xk2 = xk1 - ak =lk - lk-1.
(см. рис. 2.8). Для определенности будем считать, что на k-м шаге выбран отрезок [ак,xк2]. Тогда на (k + 1)-м шаге одной из точек деления (а именно правой) будет точка xк1. Значит, длина lk+2 отрезка, выбираемого на (k + 1)-м шаге, совпадает с длиной отрезка [ак,xк1] и верно равенство lk+2 =lk - lk-1.Подставляя найденное выражение для lk+2 в уравнение (2.9), получаем
или = 1/( — 1). Преобразуя это соотношение, приходим к квадратному уравнению , имеющему единственное положительное решение
Предположим, что отрезком минимизации унимодальной функции f(x) является [0,1], т.е. а1 = 0, b1 = 1 и l1 = 1. На первом шаге последовательного поиска (k = 1) на отрезке [0, 1] выбираем две точки и , , осуществляющие золотое сечение отрезка [0,1]. Вычисляем значения минимизируемой функции в этих точках и выполняем процедуру исключения отрезка. Если, f(x11) < f(x12), то выбираем отрезок [a1,x12], т.е. полагаем a2 = a1 = 0, b2 = x12; в противном случае выбираем отрезок [x11,b1],т.е. полагаем а2 = х11, b2 = b1=1. Кроме того, в первом случае принимаем , =x11 а во втором случае , =x12. Точка — одна из точек, осуществляющих золотое сечение отрезка [а2,b2], меньшая в первом случае и большая во втором. Если длина вновь полученного отрезка больше заданной допустимой длины интервала неопределенности, то следует перейти ко второму шагу алгоритма, на котором одна из точек x21, x22 есть точка , а вторую можно найти, например, по формуле . . На втором шаге алгоритма вычисляем лишь одно значение функции в точке, симметричной относительно середины отрезка [а2,b2]. Если же длина l2 отрезка [а2,b2], полученного после первого шага алгоритма, оказалась меньше , то поиск прекращают и полагают .
Пусть на к-м шаге, к ≥ 2, последовательного поиска по
Пусть на к-м шаге, к ≥ 2, последовательного поиска по
и вычисляем в ней значение функции. Если то и , иначе
и .
Пусть для определенности (см. рис. 2.8) и , . Если f(xk1) < f(xk2), то выбираем отрезок [ak, xk2], т.е. полагаем ak+1=ak ,bk+1=xk2, = xk1, иначе выбираем отрезок [xk1, bk], т.е. полагаем ak+1=xk1 ,bk+1=bk, = xk2. Длину lk+1 нового отрезка [ak+1, b k+1] сравниваем с и принимаем решение, продолжать поиск (при ) или нет (при ). В случае прекращения поиска полагаем .
Согласно описанию алгоритма, на первом шаге значение функции вычисляют в двух точках, а на каждом из последующих шагов вычисляют лишь одно значение функции. Поэтому после к шагов алгоритма значение функции будет вычислено в N =к + 1 точках. Поскольку после каждого шага интервал неопределенности уменьшается в раз, то для длины lk+1 отрезка [аk+1,bk+1] получаем , а зависимость длины интервала неопределенности от количества N вычисленных значений функции выражается формулой
Алгоритмы методов золотого сечения и дихотомии аналогичны. Различие состоит лишь в том, что в методе дихотомии расстояние 2δ между внутренними точками xk1, xk2 отрезка [аk,bk] на каждом к-м шаге остается неизменным, а в методе золотого сечения оно зависит от номера шага поиска и уменьшается с уменьшением длины lк отрезка по мере возрастания номера шага. Действительно, в методе золотого сечения на к-м шаге поиска внутренними точками отрезка [аk,bk] будут
, a расстояние между ними равно
Метод Фибоначчи. Пусть при поиске точки x* ∈ [0, 1],
Метод Фибоначчи. Пусть при поиске точки x* ∈ [0, 1],
Однако при любом заданном общем числе N > 2 вычисляемых значений функции можно построить еще более эффективный метод, состоящий из N — 1 шагов. Он сочетает преимущество симметричного расположения внутренних точек xk1, xk2 на отрезке [ak, bk] относительно его середины, реализованное в методах дихотомии и золотого сечения, с возможностью на каждом шаге изменять отношение lk/lk+1 длин сокращаемого и нового отрезков. Как показано при обсуждении метода золотого сечения, в случае выбора внутренних точек симметрично относительно середины отрезка для трех последовательных шагов этого метода выполняется соотношение
lk-1= lk + lk+1, к = 2,3,... (2.11)
Построение алгоритма такого метода удобнее начать с последнего шага, но предварительно уточним задачу. Располагая возможностью вычислить в N точках
, значения унимодальной на отрезке функции f(x), необходимо как можно точнее, т.е. с наименее возможной длиной интервала неопределенности, отыскать точку наименьшего значения этой функции на отрезке [0, 1].
При выполнении процедуры исключения отрезка на последнем, (N — 1)-м шаге имеем отрезок [aN-1, bN-1] длины ln-i с двумя внутренними точками xn-i и xn, симметрично расположенными относительно середины отрезка на достаточно малом расстоянии 2δ друг от друга (рис. 2.9). В этих точках вычислены значения f(xn-i) и f(xn) функции f(x). Пусть для определенности f(xn) < f(xn-i), тогда для нового отрезка [aN, bN] длины ln = ln-1 /2 + δ внутренней будет точка xn, а точка xn-1 совпадет с одним из его концов.
В такой ситуации при выборе = xn длина интервала неопределенности
В такой ситуации при выборе = xn длина интервала неопределенности
lN-2 = lN-1+ lN =3lN - 2δ, lN-3 = lN-2+ lN-1 =5lN - 4δ
lN-4 = lN-3+ lN-2 =8lN - 6δ, lN-5 = lN-4+ lN-3 =13lN - 10δ
и в общем виде
где коэффициенты Fm определены рекуррентным соотношением
Так как при К = N — 1 длина ln-k = l1= 1 отрезка [0,1] известна, то из (2.12) можно найти длину интервала неопределенности.
Существует алгоритм метода прямого поиска, удовлетворяющий соотношению (2.14).
Все коэффициенты Fm принадлежат множеству натуральных чисел, и их называют
Все коэффициенты Fm принадлежат множеству натуральных чисел, и их называют
Метод, использующий числа Фибоначчи для выбора длин отрезков lk, а значит, и точек в которых вычисляют значения минимизируемой функции, называют методом Фибоначчи (иногда — оптимальным последовательным поиском). Если на первом шаге поиска (к = 1, К = N — 1) интервал неопределенности имеет длину l1, то в соответствии с (2.12) и (2.14) длина l2 нового отрезка [а1, b2] равна
Опишем алгоритм метода, пренебрегая малой величиной δ, т.е. принимая
Несложно проверить, что в этом случае выполнение процедуры исключения отрезка на последнем, (N — 1)-м шаге поиска приводит к совпадению внутренних точек xN-1 и xN (см. рис. 2.9).
Отметим, что уже при N = 11 имеем F12/F11 = 144/89 ≈ 1,617978, а при N = 21 получаем F22/F21 = 17711/10946 ≈ 1,618034, что совпадает с отношением золотого сечения с точностью до 10-6. Таким образом, на первом шаге длина исходного отрезка уменьшается практически так же, как и в методе золотого сечения.
При l1 = 1 из (2.15) находим l2= Fn/Fn+1. Таким
При l1 = 1 из (2.15) находим l2= Fn/Fn+1. Таким
причем расстояние между ними будет равно
После выполнения на этом шаге процедуры исключения отрезка одна из точек х1, х2 будет граничной точкой нового отрезка [a2,a1], а другая — его внутренней точкой, которую обозначим . Вторая внутренняя точка на этом отрезке должна быть выбрана симметрично точке относительно его середины. Аналогично происходит выбор второй внутренней точки нового отрезка на всех последующих шагах поиска.
На к-м шаге в соответствии с равенством (2.12), в котором следует положить К = N — к, и равенством (2.14) длина отрезка [ak , bk] равна lk = FN+2-k/ FN+1 и происходит ее уменьшение в lk / lk+1= FN+2-k/FN+1-k pаз. Если внутренние точки на этом отрезке обозначить , то проведенные рассуждения позволяют написать
Подчеркнем, что реализация метода Фибоначчи предполагает априорное задание требуемого количества N вычисляемых значений функции (или количества шагов поиска). Этот параметр необходим для реализации первого шага алгоритма при выборе точек х11 и х12 деления отрезка [a1,b1]. Если параметр N по каким-либо причинам не может быть задан заранее, следует использовать другие методы, например дихотомии или золотого сечения.


![Функцию f(x) называют унимодальной функцией на отрезке [а, b], если существует](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307999/slide-3.jpg)









![Из этого равенства выводим следующую формулу длины lk отрезка [ак ,bк],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307999/slide-13.jpg)



![Метод Фибоначчи. Пусть при поиске точки x* ∈ [0, 1], в](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307999/slide-17.jpg)



 Механизмы ввода и вывода информации. Понятие сериализации
Механизмы ввода и вывода информации. Понятие сериализации Топология сетей. Тест
Топология сетей. Тест Состав Центрально-Чернозёмного района
Состав Центрально-Чернозёмного района Логарифмические уравнения - презентация по Алгебре_
Логарифмические уравнения - презентация по Алгебре_ Мышление формирует нашу жизнь
Мышление формирует нашу жизнь Система управления работой двигателя автомобиля с разработкой микропроцессорного устройства управления расходом топлива
Система управления работой двигателя автомобиля с разработкой микропроцессорного устройства управления расходом топлива «Колл Перформанс»
«Колл Перформанс»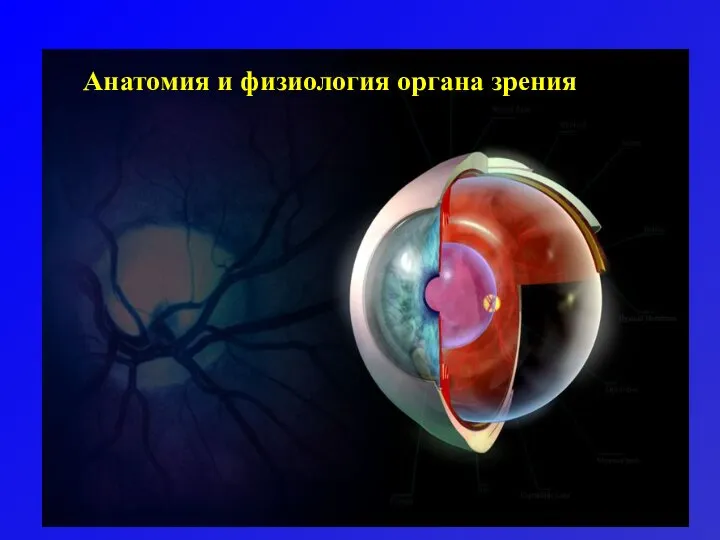 Анатомия и физиология органа зрения
Анатомия и физиология органа зрения  Геометрические характеристики плоских сечений
Геометрические характеристики плоских сечений Аттестационная работа. Программа «Мой край – Солнечная Бурятия»
Аттестационная работа. Программа «Мой край – Солнечная Бурятия» Организация мероприятий по обеспечению безопасности в образовательном учреждении ГРАЖДАНСКАЯ ОБОРОНА
Организация мероприятий по обеспечению безопасности в образовательном учреждении ГРАЖДАНСКАЯ ОБОРОНА Язык SMS. Специфика письменного печатного общения
Язык SMS. Специфика письменного печатного общения Политология, как наука о политике и ее взаимоотношениях с обществом
Политология, как наука о политике и ее взаимоотношениях с обществом Японское боевое искусство дзюдо
Японское боевое искусство дзюдо Откуда появилась матрешка
Откуда появилась матрешка Записи
Записи Вебинар «Негатив – не приговор» Работа с негативом в социальных сетях и на тематических форумах
Вебинар «Негатив – не приговор» Работа с негативом в социальных сетях и на тематических форумах Политические идеологии
Политические идеологии Как празднуют Новый год в разных странах мира
Как празднуют Новый год в разных странах мира Бонус от Катерины Красной специально для Тема: Shopper. Я эксперт!
Бонус от Катерины Красной специально для Тема: Shopper. Я эксперт! Чистый оборотный капитал (ЧОК)
Чистый оборотный капитал (ЧОК) Профессиональная династия Масалитиных МОУ «Гимназия № 1» г. Кемерово Масалитина Мария, 4 класс
Профессиональная династия Масалитиных МОУ «Гимназия № 1» г. Кемерово Масалитина Мария, 4 класс Международные отношения и внешняя политика
Международные отношения и внешняя политика  Секция: футбол
Секция: футбол Размышления о написании 8-го раздела основной образовательной программы ОУ Секция районной конференции 26 января 2011
Размышления о написании 8-го раздела основной образовательной программы ОУ Секция районной конференции 26 января 2011 Регуляция дыхания
Регуляция дыхания Исследовательская работа «Комнатные растения в классе»
Исследовательская работа «Комнатные растения в классе» ВВЕДЕНИЕ В ТОКСИКОЛОГИЮ
ВВЕДЕНИЕ В ТОКСИКОЛОГИЮ