Содержание
- 2. Цель Целью данной главы является ознакомление исследователя с основными методами статистической обработки данных, а также с
- 3. Схема экспериментального исследования и типы обработки результатов
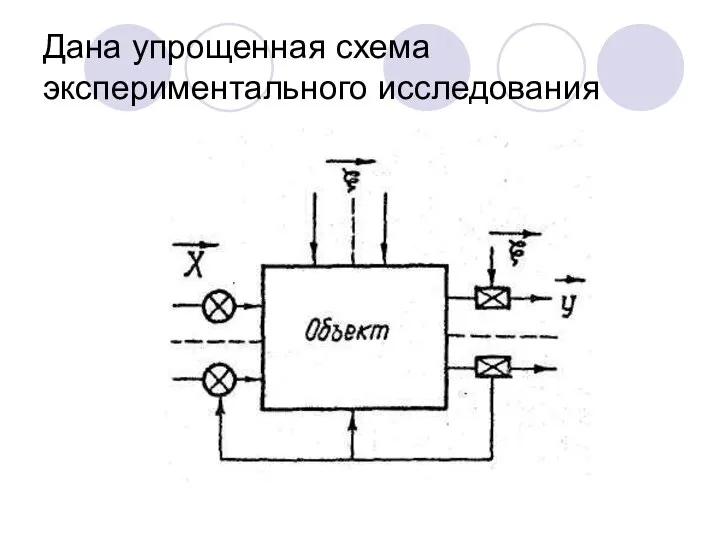
- 4. Дана упрощенная схема экспериментального исследования
- 5. Обозначая через вектор входа, будем в дальнейшем представлять его массивом х = х[n0, nf], представленным в
- 6. Например, ясно, что влияние измерительного прибора-термометра на температуру жидкости в большом баке несравнимо мало в сравнении
- 7. Например , измерение температуры термометром или измерение скорости через длину отрезка и времени его прохождения. Ясно,
- 8. Погрешности или ошибки в первом приближении классифицируются следующим образом: 1. Грубые, или промахи. Они относительно легко
- 9. Типы обработки результатов измерений
- 10. Задачи обработки опытных данных условно можно разбить на две группы: 1. Определяется значение одной величины х.
- 11. Определение значений одной величины
- 12. Пример В табл. 1 приведены результаты измерения некоторой величины. Требуется определить доверительные интервалы в зависимости от
- 13. Производим вычисления х = 172,6/16 = 10,76;
- 14. По таблицам Стьюдента-Фишера находим, что при f = 15 и Р = 0,95 t = 1,753
- 15. Рассмотрим обратную задачу. Пусть даны доверительные интервалы Д=±10% и Р=0,95. Требуется таким образом определить выборочную среднюю
- 16. Составим с этой целью таблицу 2, заполняя ее строки, начиная а второй, по приведенным выше формулам.
- 17. Из данных таблицы 2 видно, что Р вначале колеблется, а при n0=6 его значение стабилизируется, достигая
- 18. В тех случаях, когда х меняется в больших пределах строят гистограмму и определяют числовые моменты более
- 19. Определение связи
- 20. Качественные исследования - анализ влияния некоторых факторов на выходную величину тогда, когда эти факторы нельзя представить
- 21. Рассмотрим сущность МНК на примере линейной функции у = а0+а1х, для которой заданы наборы значений фактора
- 22. Для этого следует минимизировать величину
- 23. необходимо выполнить условия или
- 24. После дифференцирования и упрощения выражений получим систему уравнений
- 25. Статистическая проверка гипотез. Критерии оценки качества аппроксимации
- 26. Статистическая проверка гипотез Рассмотрим этот метод на примере однофакторного дисперсионного анализа. Пусть имеется ряд значений случайной
- 27. Сумму квадратов результатов наблюдений SCt можно представить в виде суммы квадратов SCi внутри каждой группы вокруг
- 28. Эти выражения можно представить в другом виде
- 29. Для вычисления на компьютере: где SCe — доля общей суммы квадратов, объясняемая гипотезой и возникающая из-за
- 30. Суммы квадратов сопоставляются с учетом степеней свободы. Оценки дисперсии равны соответственно В тех случаях, когда SCe
- 31. Общий случай Дано: генеральная совокупность и две выборки объема n1 и n2. Мы хотим проверить гипотезу
- 32. Общий случай - дисперсия - выборочные дисперсии 1 и 2 и В математической статистике рассматриваются случайные
- 33. Оценка адекватности аппроксимации эмпирического выражения Как известно, при линейной аппроксимации у=а0+а1х для оценки ее качества используют
- 34. Существуют и более эффективные критерии оценки аппроксимации. Например, выдвигая гипотезу Н0 о той что ошибка аппроксимации
- 35. а величина Se определяется из опыта, где nk число коэффициентов аппроксимирующего выражения, для принята гипотезы или
- 36. Второй критерий базируется на использовании выражении характеризующего относительное уменьшение неопределенности при аппроксимации статистических данных эмпирческой формулой.
- 37. Величина критерия І2 находится в диапазоне 0÷1 и чем ближе к единице это значение, тем меньше
- 38. Отметим, что дисперсия аппроксимации при малых fi=n0-nk может стать больше, чем , и тогда его величина
- 39. Применение относительной ошибки для оценки аппроксимации Часто возникает вопрос о целесообразности многократного повторения опытов для нахождения
- 40. Применение относительной ошибки для оценки аппроксимации Обозначим через V∞ (%) допустимую вариацию или относительную ошибку (2,
- 41. При числе степеней свободы f = n0-nk → ∞, т.е. исходя из предположения, что символ ∞
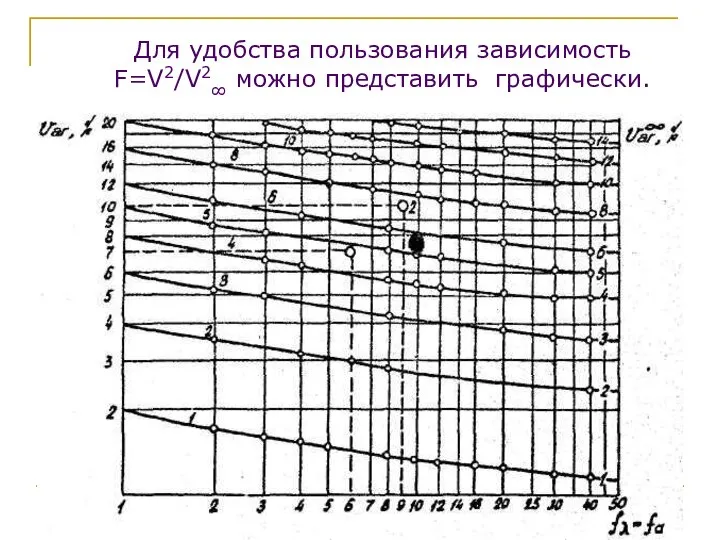
- 42. Для удобства пользования зависимость F=V2/V2∞ можно представить графически.
- 43. На рисунке приведен график критерия Фишера, где по оси абсцисс f1=fa откладывается число степеней свободы числителя
- 44. Математическое обеспечение для обработки результатов наблюдений и экспериментов
- 45. В пределах настоящего курса не ставилась цель показать все множество формул, процедур и программ современной прикладной
- 46. Программа "ПОЛИНОМ" Программа "Полином" предназначена для получения статистических (регрессионных) зависимостей ya=F(х1,...,ХHF) величины уа ряда независимых величин-факторов,
- 47. Программа может быть использована и для нелинейных случаев при соответствующей линеаризации. Особенность программы заключается в том,
- 48. Программа "Мини" Программа предназначена для поиска минимума функции любого типа: линейной или нелинейной, с ограничениями или
- 49. Подпрограмма "Шаг" Эта подпрограмма является основным элементом детерминированного метода, в котором происходит поиск локального минимума функции
- 50. "ФКВ" - программа фильтрации исходных данных, корреляции между независимыми факторами и оценки их влияния Часто при
- 51. Иногда при проведении наблюдений или при неправильно спланированном эксперименте имеет место сильная корреляция между "независимыми факторами.
- 52. Наконец, часто бывает полезным оценивать влияние независимых переменных х (no , nf ) на зависимую у
- 53. Программа «Дисперсия» Дисперсионный анализ служит для оценки влияния на какой-то процесс факторов, которые не могут быть
- 54. Например, если требуется оценить точность измерения одной и той же величины различными аппаратами А, В, С,…
- 55. Программа "УРАВНЕНИЕ" Эта программа служит для решения линейных или нелинейных уравнений методом половинного деления. Предлагаемый вариант
- 56. Если знак двух последующих значений у одинаковый, ход действия продолжается еще на одни шаг. Если знак
- 57. Программа "Фильтр" Эта программа предназначена для решения следующей задачи. Дана запись некоторой величины у (например, траектория
- 59. Скачать презентацию




















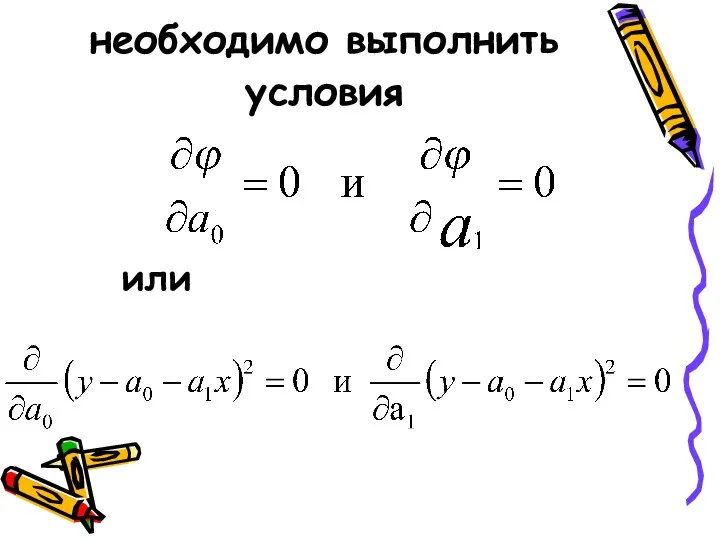

































 Демографическая ситуация в Приволжском федеральном округе От переписи населения 2004 года численность жителей округа сократилась к началу 2011 года на 913,5 тыс. человек, или на 2,9 процента и составила 30241,5 тыс. человек. З
Демографическая ситуация в Приволжском федеральном округе От переписи населения 2004 года численность жителей округа сократилась к началу 2011 года на 913,5 тыс. человек, или на 2,9 процента и составила 30241,5 тыс. человек. З Введение в предмет физики. Кинематика материальной точки
Введение в предмет физики. Кинематика материальной точки Презентация Требования к лицам, поступающим на гражданскую службу в таможенные органы России
Презентация Требования к лицам, поступающим на гражданскую службу в таможенные органы России  Система Национальных Счетов ВВП (Gross Domestic Product) ВНП (Gross National Product) Для расчета ВВП может быть использовано три метода: по расхода
Система Национальных Счетов ВВП (Gross Domestic Product) ВНП (Gross National Product) Для расчета ВВП может быть использовано три метода: по расхода Расширенный поиск в НКРЯ
Расширенный поиск в НКРЯ Выполнили: студентки 3-го курса ФТД группы Т-084 Лоренгель Татьяна Барякинская Екатерина Пикалёва Валерия Шатикова Ирина
Выполнили: студентки 3-го курса ФТД группы Т-084 Лоренгель Татьяна Барякинская Екатерина Пикалёва Валерия Шатикова Ирина  Муниципальное общеобразовательное учреждение «МОУ СОШ № 6 г.Вольска Саратовской области» Иконы Богородицы в истории России Вы
Муниципальное общеобразовательное учреждение «МОУ СОШ № 6 г.Вольска Саратовской области» Иконы Богородицы в истории России Вы мое призвание УЧИТЬ!!! - презентация для начальной школы
мое призвание УЧИТЬ!!! - презентация для начальной школы Тест по МХК. 9 класс. Азбука архитектуры
Тест по МХК. 9 класс. Азбука архитектуры Получение и передача переменного электрического тока. Трансформатор
Получение и передача переменного электрического тока. Трансформатор Ремонт столовых у буфетов ДЦ-1 КХЦ
Ремонт столовых у буфетов ДЦ-1 КХЦ Презентация на тему "Развитие зародыша и плода. Беременность и роды" - скачать презентации по Медицине
Презентация на тему "Развитие зародыша и плода. Беременность и роды" - скачать презентации по Медицине 12 апреля - Международный день космонавтики Сегодня весь мир отмечает знаменательный для человечества день! Ровно 50 лет назад состо
12 апреля - Международный день космонавтики Сегодня весь мир отмечает знаменательный для человечества день! Ровно 50 лет назад состо Важнейшее христианское таинство - крещение
Важнейшее христианское таинство - крещение Будда реальний і Будда із легенд
Будда реальний і Будда із легенд Тема: « Предмет и задачи этнопедагогики»
Тема: « Предмет и задачи этнопедагогики» Нормы таможенного законодательства XIX века. Подготовила: Шмакова Татьяна, ЮФ-104
Нормы таможенного законодательства XIX века. Подготовила: Шмакова Татьяна, ЮФ-104 Классификация организмов. История создания современной классификации
Классификация организмов. История создания современной классификации Крито-микенская культура (III-II тыс. до н. э.)
Крито-микенская культура (III-II тыс. до н. э.) Черхаркашглотская Священная Империя
Черхаркашглотская Священная Империя Информационные технологии в сфере сервиса и туризма
Информационные технологии в сфере сервиса и туризма Механизмы отогенеза
Механизмы отогенеза  Актерское мастерство
Актерское мастерство Процессор. Что такое процессор?
Процессор. Что такое процессор? Программа праздника 8 Марта
Программа праздника 8 Марта Презентация на тему "Черты современного урока с точки зрения повышения познавательной активности учащихся" - скачать презент
Презентация на тему "Черты современного урока с точки зрения повышения познавательной активности учащихся" - скачать презент Инструкция по совершенствованию регионализации перинатальной помощи в Республики
Инструкция по совершенствованию регионализации перинатальной помощи в Республики Российско-сирийские отношения
Российско-сирийские отношения