Содержание
- 2. 1.Ортогональная матрица Определение 1.1. Действительная квадратная матрица Q такая что Q−1 = QT называется ортогональной матрицей.
- 3. Пример .
- 4. Теорема 1.3. Следующие утверждения эквивалентны для n×n матрицы A. (a) A – ортогональная матрица. (b) Строки
- 5. Доказательство. Доказательство проведем для одного из пунктов, остальные доказываются аналогично. Предположим выполняется пункт (а). Докажем пункт
- 6. Теорема 1.4. (свойства ортогональной матрицы). (a) Матрица, обратная к ортогональной, также является ортогональной. (b) Произведение ортогональных
- 7. Доказательство.
- 8. Теорема 1.5. Матрица перехода от одной ортонормированной базы к другой в евклидовом пространстве является ортогональной матрицей.
- 9. 2. Ортогональный оператор Определение 2.1. Линейный оператор в n-мерном евклидовом пространстве V называется ортогональным, если он
- 10. Теорема 2. Ортогональный оператор в n-мерном евклидовом пространстве сохраняет скалярное произведение. Доказательство. Сравниваем Получаем QED
- 11. Теорема 2.3. Линейный оператор в n-мерном евклидовом пространстве V является ортогональным т. и т.т.к. матрица Т
- 12. Доказательство. (b1) = t11 b1 + t21 b2 + … + tn1 bn (b2) = t12
- 14. Скачать презентацию

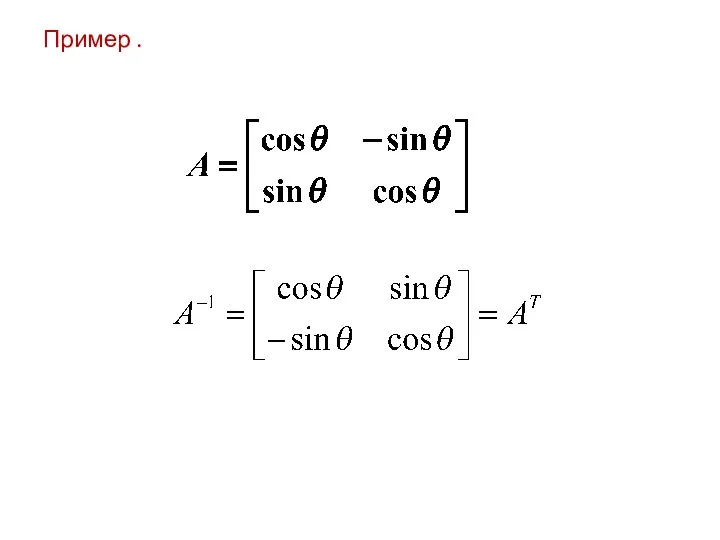









 Движения для здоровья. Влияние физических упражнений на организм
Движения для здоровья. Влияние физических упражнений на организм Технология активизации проектной деятельности
Технология активизации проектной деятельности Презентация Общевоинские уставы Вооруженных Сил РФ — закон воинской жизни
Презентация Общевоинские уставы Вооруженных Сил РФ — закон воинской жизни  Достопримечательности Китая
Достопримечательности Китая Современный подросток на приходе: что упускаем и что можем сделать
Современный подросток на приходе: что упускаем и что можем сделать Национальный японский костюм
Национальный японский костюм CУБД. Этапы проектирования. Создание таблиц, работа с данными в таблице. Построение запросов
CУБД. Этапы проектирования. Создание таблиц, работа с данными в таблице. Построение запросов Инженерный менеджмент и информационные технологии. (Лекция 1)
Инженерный менеджмент и информационные технологии. (Лекция 1) Подготовили: Порошина Л.В., Анкудинова М.А., гр.Ю-102
Подготовили: Порошина Л.В., Анкудинова М.А., гр.Ю-102  Cherrikita. Что же это за канал?
Cherrikita. Что же это за канал? Залоговое право и поручительство в практике верховного суда РФ
Залоговое право и поручительство в практике верховного суда РФ Русские народные традиции и обряды. (Часть 1)
Русские народные традиции и обряды. (Часть 1) Дискуссия об английском артикле: перспектива и ретроспектива
Дискуссия об английском артикле: перспектива и ретроспектива Банковский менеджмент (1)
Банковский менеджмент (1) Наука и философия
Наука и философия Технология получения электронной аппаратуры для работы в условиях экстремальных ударных нагрузок
Технология получения электронной аппаратуры для работы в условиях экстремальных ударных нагрузок Без названия
Без названия ФИАТНЫЕ деньги Петрова М.А.
ФИАТНЫЕ деньги Петрова М.А. Художественные системы в проектировании одежды
Художественные системы в проектировании одежды Ангелы. Представления об ангелах в исламе
Ангелы. Представления об ангелах в исламе Штриховой код - штрих-ко́д
Штриховой код - штрих-ко́д  Оlimpic Champion in Ukraine
Оlimpic Champion in Ukraine Защита авторских прав на контент
Защита авторских прав на контент Строение зрительного анализатора.
Строение зрительного анализатора. Презентация на тему "Восковые моделировочные материалы применяемые в клинике ортопедической стоматологии (+)" - скачать презе
Презентация на тему "Восковые моделировочные материалы применяемые в клинике ортопедической стоматологии (+)" - скачать презе Введение в теорию оптимизации. Лекция1
Введение в теорию оптимизации. Лекция1 Презентация Значение теории относительности Эйнштейна
Презентация Значение теории относительности Эйнштейна Замісник (проксі). Патерни проектування
Замісник (проксі). Патерни проектування