Содержание
- 2. 1. Симметрическая матрица Определение 1.1. Действительная матрица A называется симметрической, если Из определения следует, что симметрическая
- 3. Примеры. симметрична. симметрична.
- 4. Теорема 1.2. Пусть A – симметрическая матрица, тогда все собственные значения этой матрицы – действительные числа.
- 6. 2. Пусть v – комплексный собственный вектор матрицы А, отвечающий действительному собственному значению λ: А v
- 7. 2. Симметрический оператор Определение 2.1. Линейный оператор евклидова пространства Е называется симметрическим, если для любых векторов
- 8. Теорема 2.2. Линейный оператор в евклидовом пространстве является симметрическим тогда и только тогда, когда его матрица
- 9. . Пусть - произвольный ортонормированный базис, А – симметрическая матрица оператора , u,v – два произвольных
- 10. . Следствие2.3. (1) Все собственные значения симметрического оператора – действительные числа. (2) Любой симметрический оператор имеет
- 11. Теорема 2.4. Собственные векторы симметрического линейного оператора, соответствующие различным собственным значениям, ортогональны. Доказательство. Пусть Тогда
- 12. Теорема 2.5. Для любого симметрического линейного оператора евклидова пространства существует ортонормированный базис пространства , составленный из
- 13. Перейдем к пространству Е размерности n. Пусть b – собственный вектор, отвечающий некоторому собственному значению. Нормируем
- 14. Следствие 2.6. Матрица симметрического линейного оператора с помощью соответственного выбора ортонормированного базиса, может быть приведена к
- 15. Пример. В некотором ортонормированном базисе в R3 линейное преобразование φ задано матрицей Найти для φ ортонормированный
- 16. Шаг2. Нахождение СВ Система уравнений для собственных векторов: В качестве первого вектора берем Второй линейно независимый
- 18. Скачать презентацию



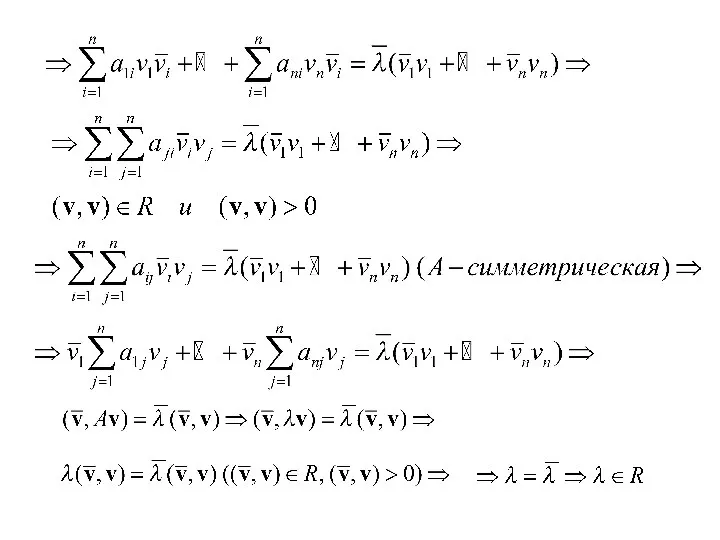











 Авторское право в экскурсионном деле
Авторское право в экскурсионном деле Презентация Правовой статус иностранных граждан, лиц без гражданства, беженцев и вынужденных переселенцев в РФ.
Презентация Правовой статус иностранных граждан, лиц без гражданства, беженцев и вынужденных переселенцев в РФ. Ф.А.Искандер - советский и российский прозаик и абхазский поэт
Ф.А.Искандер - советский и российский прозаик и абхазский поэт «Патриотизм как нравственная основа жизнеспособности государства»
«Патриотизм как нравственная основа жизнеспособности государства» В детсаде хорошим другом в твоём представлении был тот, кто давал тебе красный мелок, когда последним оставшимся был уродский чёрн
В детсаде хорошим другом в твоём представлении был тот, кто давал тебе красный мелок, когда последним оставшимся был уродский чёрн Возбудители брюшного тифа и паратифов
Возбудители брюшного тифа и паратифов  Тендерная документация в строительстве
Тендерная документация в строительстве Агния Барто - творчество
Агния Барто - творчество лекция 3
лекция 3 Flash Cards
Flash Cards Что легенда мне расскажет? Выполнил: ученик 6-Б Сердюк Сергей
Что легенда мне расскажет? Выполнил: ученик 6-Б Сердюк Сергей Тема: Права и свободы человека и гражданина по Конституции Российской Федерации.
Тема: Права и свободы человека и гражданина по Конституции Российской Федерации. Гемостаз в норме
Гемостаз в норме Совесть в деятельности юриста
Совесть в деятельности юриста Основы языка Visual Basic. Функции
Основы языка Visual Basic. Функции МБОУ «Торгашинская СОШ» Урок – практикум в 9 классе по алгебре. Тема: «Квадратный трехчлен». Учитель Заха
МБОУ «Торгашинская СОШ» Урок – практикум в 9 классе по алгебре. Тема: «Квадратный трехчлен». Учитель Заха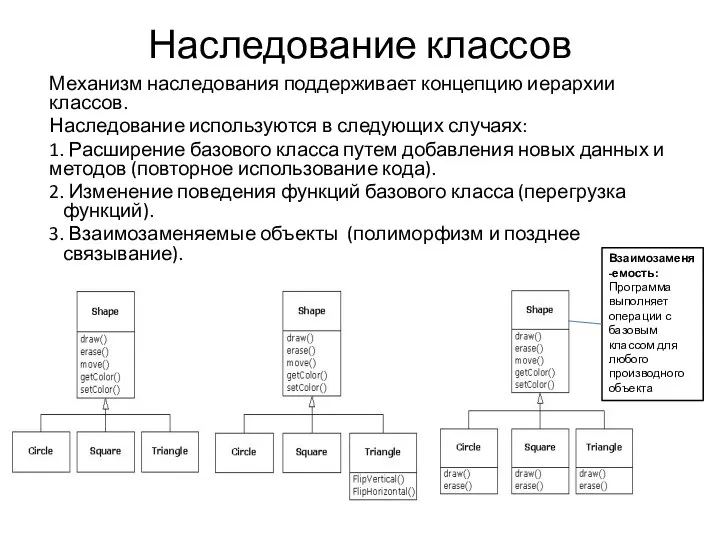 Наследование классов. Спецификация базового класса. (Лекция 3)
Наследование классов. Спецификация базового класса. (Лекция 3) В рамках реализации постановления правительства Ростовской области «Каким должен быть детский дом сегодня?»
В рамках реализации постановления правительства Ростовской области «Каким должен быть детский дом сегодня?» МОНИТОРИНГ СТОМАТОЛОГИЧЕСКОЙ ЗАБОЛЕВАЕМОСТИ У ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА И ПУТИ ПРОФИЛАКТИКИ
МОНИТОРИНГ СТОМАТОЛОГИЧЕСКОЙ ЗАБОЛЕВАЕМОСТИ У ДЕТЕЙ ДОШКОЛЬНОГО ВОЗРАСТА И ПУТИ ПРОФИЛАКТИКИ  Citrus Festival a Methone
Citrus Festival a Methone Пернатые изобретатели Подготовила: учитель начальных классов Белова Лариса Сергеевна, МОУ ООШ №7 города Белово
Пернатые изобретатели Подготовила: учитель начальных классов Белова Лариса Сергеевна, МОУ ООШ №7 города Белово . Понятие информационного процесса. Сбор и обработка информации
. Понятие информационного процесса. Сбор и обработка информации СОЦИАЛЬНО-ПЕДАГОГИЧЕСКОЕ ПАРТНЕРСТВО КАК СРЕДСТВО КОРРЕКЦИИ ДЕВИАНТНОГО ПОВЕДЕНИЯ Заместитель директора по ВР ГОУ С
СОЦИАЛЬНО-ПЕДАГОГИЧЕСКОЕ ПАРТНЕРСТВО КАК СРЕДСТВО КОРРЕКЦИИ ДЕВИАНТНОГО ПОВЕДЕНИЯ Заместитель директора по ВР ГОУ С Самый масштабный интерактивный проект INSTAGIRLS
Самый масштабный интерактивный проект INSTAGIRLS Тема 16. Управление производственными операциями и предоставлением услуг
Тема 16. Управление производственными операциями и предоставлением услуг  Напряженно-деформированное состояние балок при изгибе
Напряженно-деформированное состояние балок при изгибе Подходы М.Фридмана к определению социальной ответственности бизнеса Работу выполнили Студентки 2-го курса Экономического факул
Подходы М.Фридмана к определению социальной ответственности бизнеса Работу выполнили Студентки 2-го курса Экономического факул Национальные музыкальные инструменты коми
Национальные музыкальные инструменты коми