Содержание
- 2. Геометрическая интерпретация Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования,
- 3. Геометрическая интерпретация Возьмём на плоскости декартову систему координат и каждой паре чисел (x1, x2) поставим в
- 4. Геометрическая интерпретация Рассмотрим теперь, какие области соответствуют неравенствам вида a1x1+a1x2≤b. Сначала рассмотрим область, соответствующую равенству a1x1+a1x2=b.
- 5. Геометрическая интерпретация Дальше через эти две точки можно по линейке провести прямую линию (смотри рисунок 2).
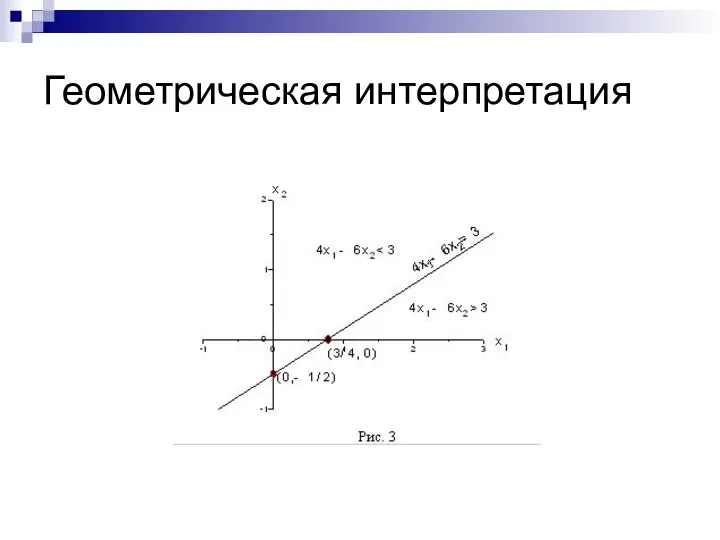
- 6. Геометрическая интерпретация Эта построенная прямая разбивает всю плоскость на две полуплоскости. В одной её части a1x1+a1x2
- 7. Геометрическая интерпретация
- 8. Геометрическая интерпретация Вернёмся теперь к задаче линейного программирования. Там имеют место m неравенств a11x1+a12x2≤b1, a21x1+a22x2≤b2, ……………….
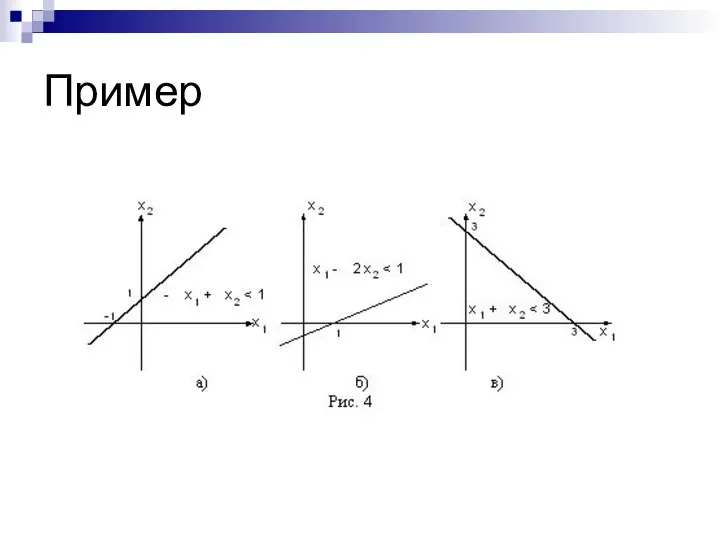
- 9. Пример Найти допустимую область задачи линейного программирования, определяемую ограничениями -x1+x2≤1, x1-2x2≤1, x1+x2≤3, x1≥0, x2≥0.
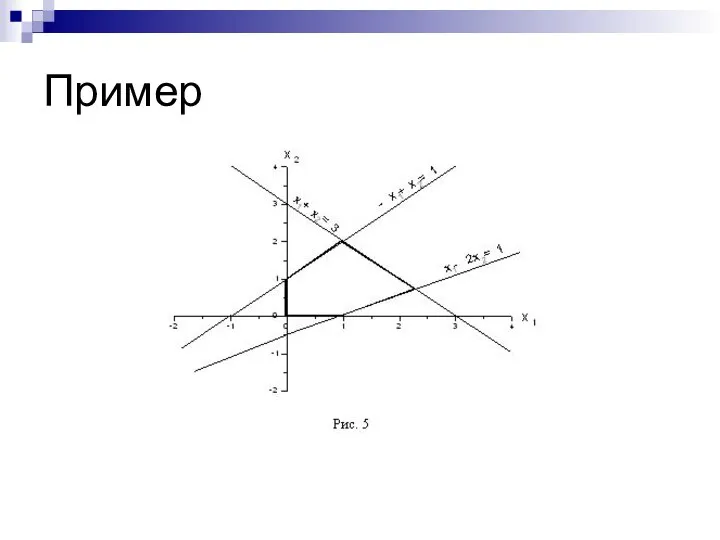
- 10. Пример
- 11. Пример
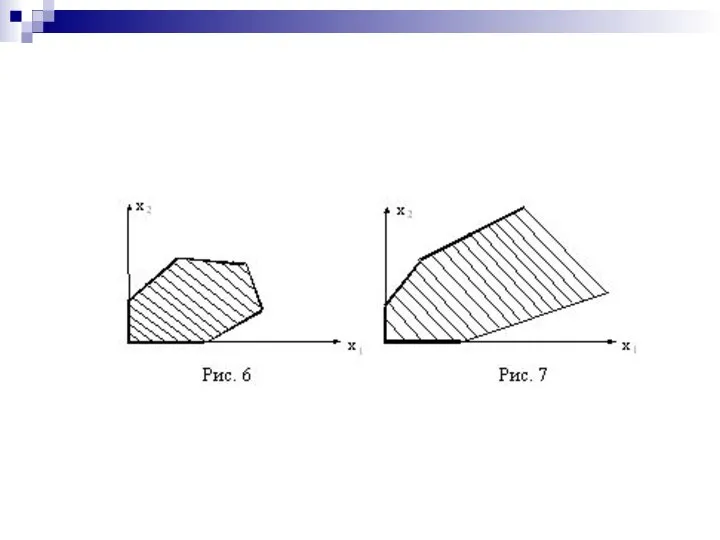
- 12. Возможные случаи Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (см. рис. 6). Неосновной
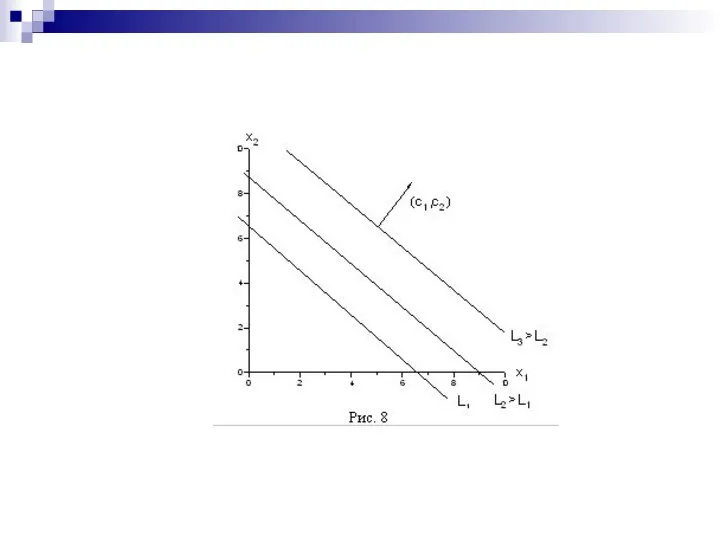
- 14. Геометрическая интерпретация Вернёмся теперь к исходной задаче линейного программирования. В ней, кроме системы неравенств, есть еще
- 16. Решение А теперь сведем всё вместе. Итак, надо решить задачу c1x1+c2x2→max a11x1+a12x2≤b1, a21x1+a22x2≤b2, ………………. am1x1+am2x2≤bm, x1≥0;
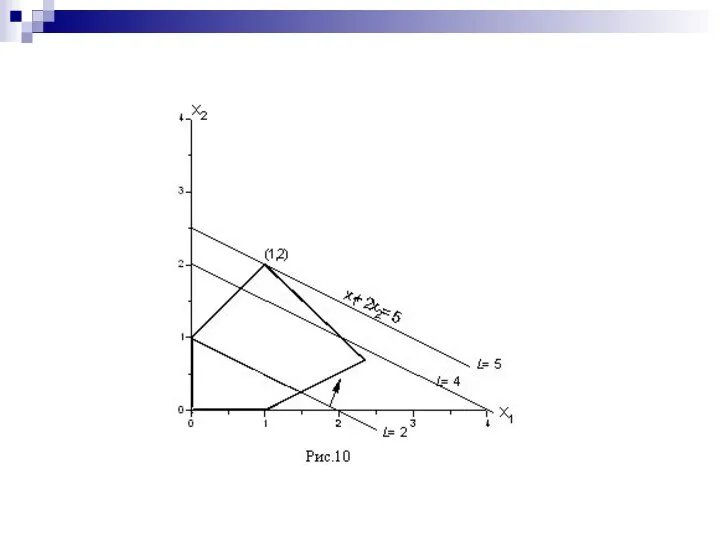
- 17. Пример Решить задачу x1+2x2→max -x1+x2≤1, x1-2x2≤1, x1+x2≤2, x1≥0; x2≥0.
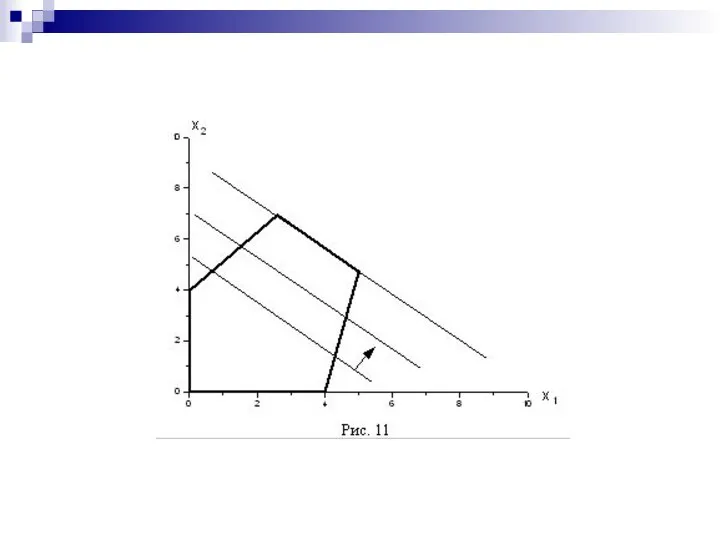
- 19. Особый случай Обратите внимание на то, что оптимальный план, как правило, соответствует какой-то вершине многоугольника, изображающего
- 22. Скачать презентацию












 Aktuelle entwicklungen in der fremdsprachendidaktik
Aktuelle entwicklungen in der fremdsprachendidaktik Витамин «С»
Витамин «С» Язык UML
Язык UML Электронды техника ќўраушылары. Заттыѕ ќўрылысы туралы негізгі тїсініктер
Электронды техника ќўраушылары. Заттыѕ ќўрылысы туралы негізгі тїсініктер Tema_5_Prestuplenia_protiv_polovoy_neprikosnovennosti_i_polovoy_svobody_lichnosti.ppt
Tema_5_Prestuplenia_protiv_polovoy_neprikosnovennosti_i_polovoy_svobody_lichnosti.ppt Выполнено Наумовым Михаилом
Выполнено Наумовым Михаилом  Исторические корни и периодизация развития континентальной правовой системы
Исторические корни и периодизация развития континентальной правовой системы Исследование методов повышения пропускной способности в сетях UMTS
Исследование методов повышения пропускной способности в сетях UMTS Русская матрёшка Декоративное рисование 8 класс Учитель ИЗО МБОУ «Западнодвинская СОШ №1» Архипова
Русская матрёшка Декоративное рисование 8 класс Учитель ИЗО МБОУ «Западнодвинская СОШ №1» Архипова АПК и ППРО Пономарева Елена Анатольевна К.п.н., доцент Москва 2010
АПК и ППРО Пономарева Елена Анатольевна К.п.н., доцент Москва 2010 Презентация "Мусоргский М.П" - скачать презентации по МХК
Презентация "Мусоргский М.П" - скачать презентации по МХК Развитие баскетбола в России
Развитие баскетбола в России Использование системы сбалансированных показателей в системе внутреннего контроля
Использование системы сбалансированных показателей в системе внутреннего контроля Охрана труда на предприятии
Охрана труда на предприятии  Баскетбол. Правила игры
Баскетбол. Правила игры Введение в Delphi. (Лекция 2)
Введение в Delphi. (Лекция 2) Финансирование инновационной деятельности
Финансирование инновационной деятельности Пересечение поверхности плоскостью
Пересечение поверхности плоскостью Понятие гражданского права, как отрасли права. Источники гражданского права
Понятие гражданского права, как отрасли права. Источники гражданского права Теплопритоки к жидкому хладагенту. Теплоподвод за счет теплопроводности твердых тел
Теплопритоки к жидкому хладагенту. Теплоподвод за счет теплопроводности твердых тел Отладочная плата MCS-51
Отладочная плата MCS-51 Искусство Италии 16 век
Искусство Италии 16 век Теория оптимальных валютных зон Кургалимова А., МЭ081
Теория оптимальных валютных зон Кургалимова А., МЭ081 Ліна Костенко
Ліна Костенко Презентация Механизм государственного регулирования внешнеторговой деятельности Исакова Елизавета
Презентация Механизм государственного регулирования внешнеторговой деятельности Исакова Елизавета Тестирование программных средств
Тестирование программных средств Моя родина - Россия 4 класс - презентация для начальной школы_
Моя родина - Россия 4 класс - презентация для начальной школы_ Международная обувная компания ECCO
Международная обувная компания ECCO