Содержание
- 2. Относительность движения Механическим движением называется изменение положения тела в пространстве с течением времени. Положение тела, а
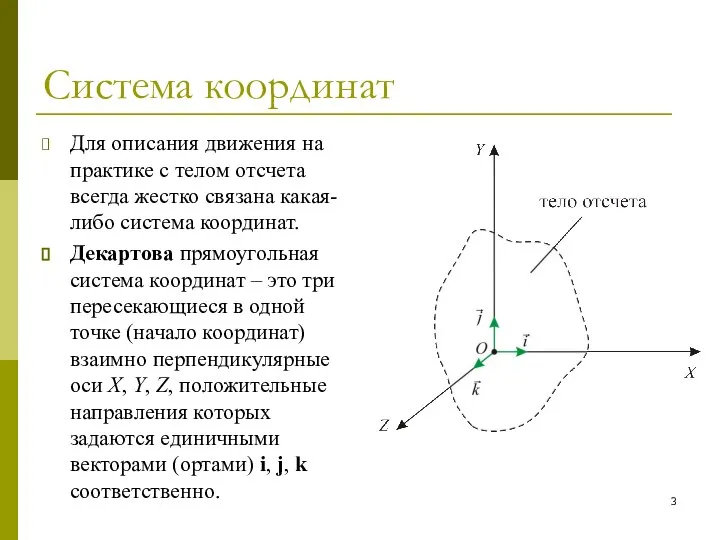
- 3. Система координат Для описания движения на практике с телом отсчета всегда жестко связана какая-либо система координат.
- 4. Координаты тела Координаты x, y, z небольшого тела P, определяют его положение в пространстве. Эти три
- 5. Измерение длины Определение координат тела в конечном счете сводится к измерению расстояний (длин отрезков). Под измерением
- 6. Измерение длины Инструментом для измерения длины может служить, например, линейка с нанесенной на нее миллиметровой шкалой
- 7. Измерение длины За единицу СИ (Международная система единиц) принят метр (м). Первоначально (с 1799 г.) за
- 8. Измерение времени Движение тел происходит в пространстве и во времени. Для его описания необходимо измерять также
- 9. Синхронизация часов Для описания механического движения необходимо пользоваться единым для всего пространства временем и, следовательно синхронизировать
- 10. Пространственно-временная система отсчета Мы установили, что для описания движения в пространстве и во времени необходимо иметь:
- 11. Постулаты классической механики о пространстве, времени и движении В классической ньютоновской механике размеры тел и промежутки
- 12. Постулаты классической механики о пространстве, времени и движении Опыт показывает, что предположения (постулаты) об абсолютности пространства
- 13. ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ 1.2 Векторный способ описания движения материальной точки
- 14. Кинематика. Выбор системы отсчета Кинематика – это раздел механики, в котором изучают способы описания движения тел,
- 15. Понятие материальной точки Реальные движения тел весьма сложны. Чтобы отвлечься от несущественных для данного движения деталей,
- 16. Понятие материальной точки Произвольное макроскопическое тело, размеры которого возможно не малы, по сравнению с характерными для
- 17. Векторный способ задания движения Рассмотрим движение частицы A в некоторой выбранной СО, начало координат которой расположено
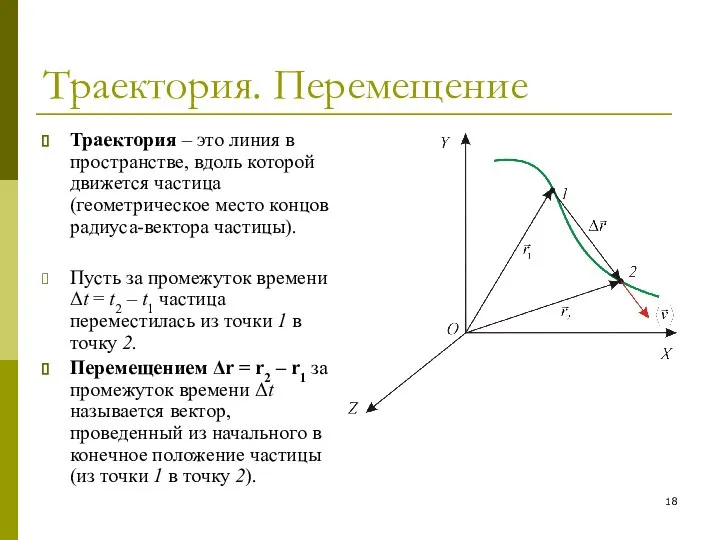
- 18. Траектория. Перемещение Траектория – это линия в пространстве, вдоль которой движется частица (геометрическое место концов радиуса-вектора
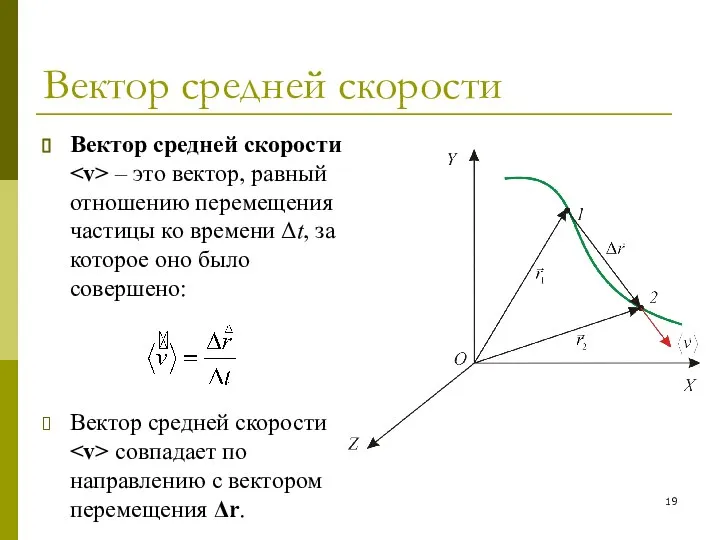
- 19. Вектор средней скорости Вектор средней скорости – это вектор, равный отношению перемещения частицы ко времени Δt,
- 20. Мгновенная скорость Пусть промежуток времени Δt стремится к нулю, тогда точка 2 траектории приближается к точке
- 21. Единица измерения скорости В СИ скорость измеряется в метрах в секунду (м/с). 1 км/ч = 1000
- 22. Ускорение Ускорением называется вектор, равный производной по времени скорости v частицы:
- 23. Прямая и обратная задачи кинематики Если зависимость радиуса-вектора от времени r(t) известна, то можно решить т.н.
- 24. ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ 1.3 Координатный способ описания движения материальной точки
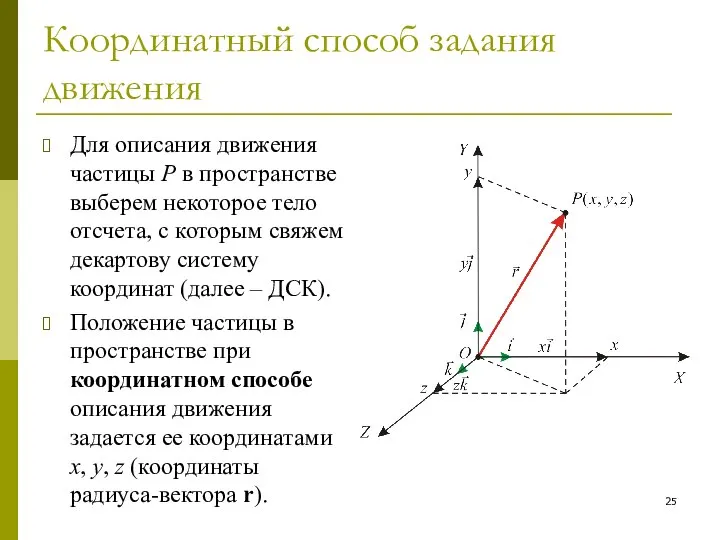
- 25. Координатный способ задания движения Для описания движения частицы P в пространстве выберем некоторое тело отсчета, с
- 26. Закон движения Законом движения называется зависимость от времени координат частицы: Между векторным и координатным способами описания
- 27. Скорость при координатном способе описания движения Скорость v, как и любой вектор, может быть представлена через
- 28. Модуль и направление вектора скорости Для каждого момента времени t можно определить модуль и направление (с
- 29. Ускорение при координатном способе задания движения Ускорение a, как и любой вектор, может быть представлен через
- 30. Модуль и направление вектора ускорения Для каждого момента времени t можно определить модуль и направление (с
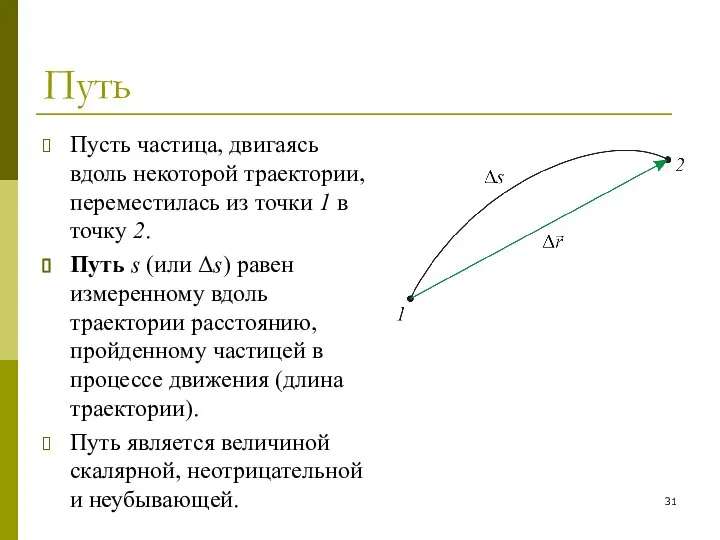
- 31. Путь Пусть частица, двигаясь вдоль некоторой траектории, переместилась из точки 1 в точку 2. Путь s
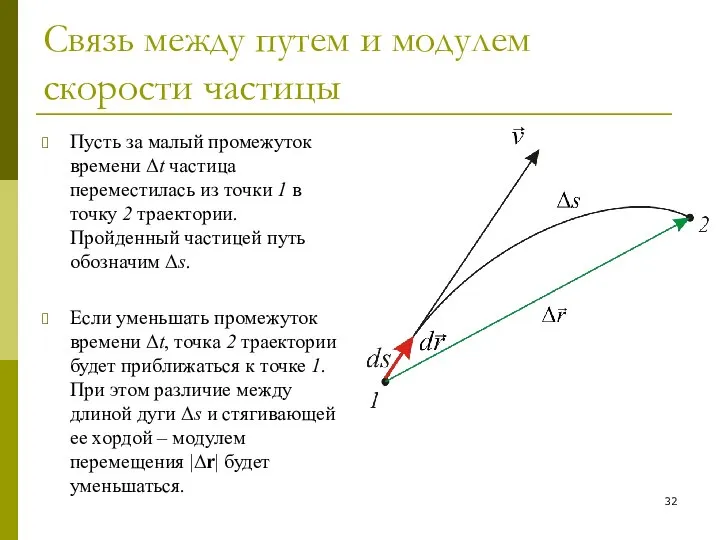
- 32. Связь между путем и модулем скорости частицы Пусть за малый промежуток времени Δt частица переместилась из
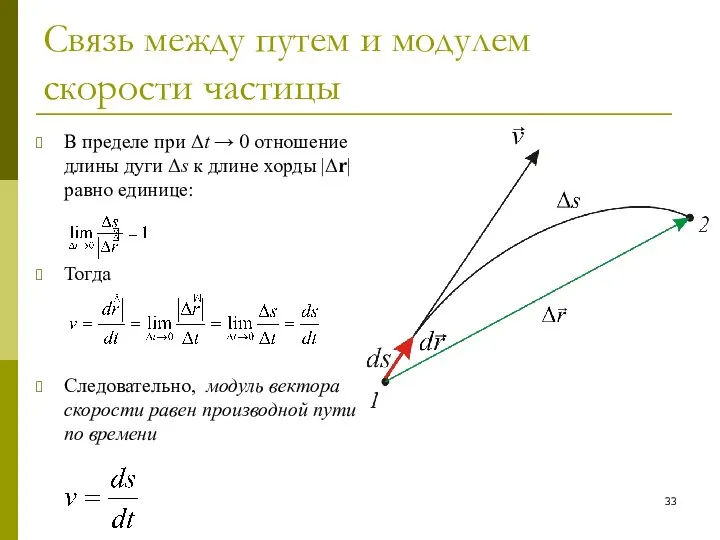
- 33. Связь между путем и модулем скорости частицы В пределе при Δt → 0 отношение длины дуги
- 34. Связь между путем и модулем скорости частицы Зная зависимость модуля скорости v от времени, можно вычислить
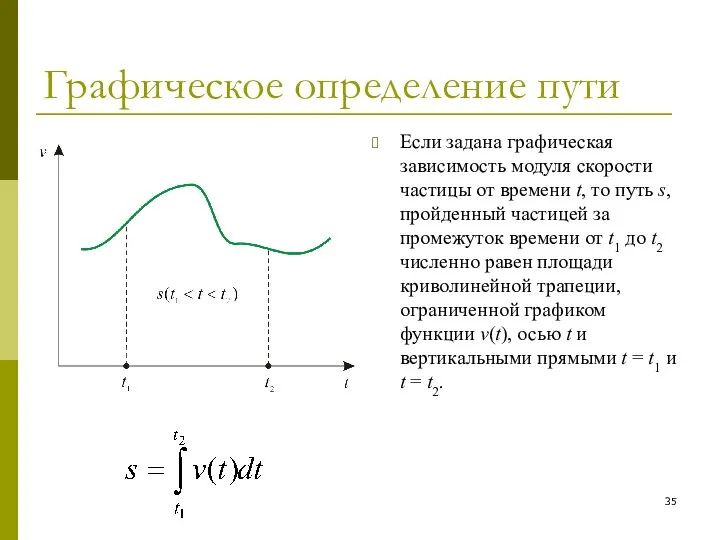
- 35. Графическое определение пути Если задана графическая зависимость модуля скорости частицы от времени t, то путь s,
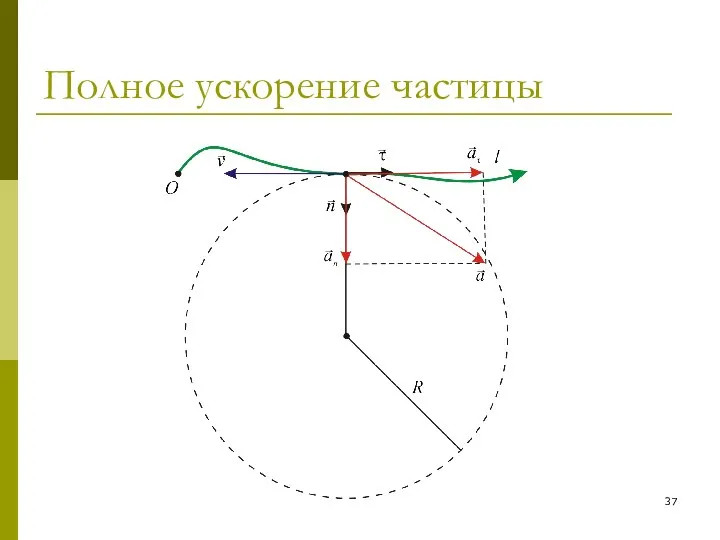
- 36. Полное ускорение частицы Полное ускорение частицы a можно представить в виде суммы двух перпендикулярных друг другу
- 37. Полное ускорение частицы
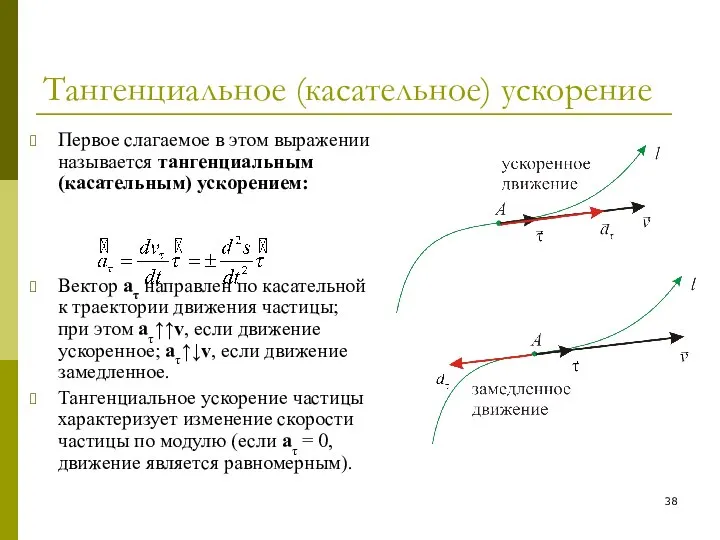
- 38. Тангенциальное (касательное) ускорение Первое слагаемое в этом выражении называется тангенциальным (касательным) ускорением: Вектор aτ направлен по
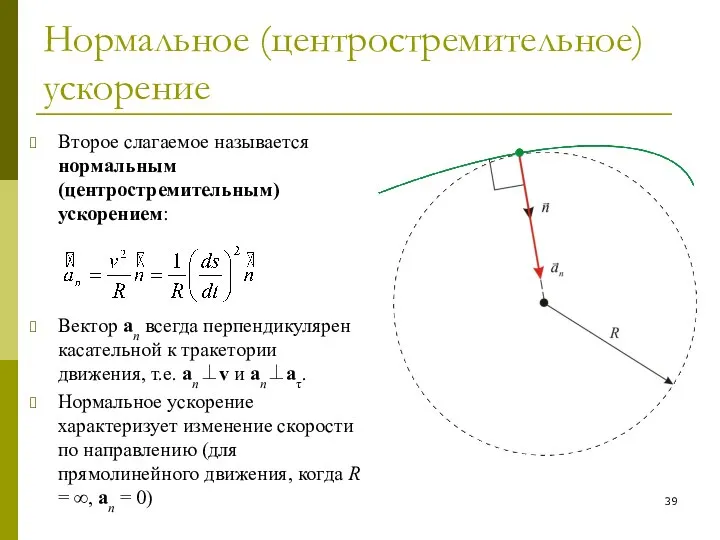
- 39. Нормальное (центростремительное) ускорение Второе слагаемое называется нормальным (центростремительным) ускорением: Вектор an всегда перпендикулярен касательной к тракетории
- 40. ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ 1.4 Твердое тело в механике. Виды движения твердого тела
- 41. Абсолютно твердое тело Абсолютно твердым телом в механике называют тело, при движении которого расстояния между любыми
- 42. Виды движения абсолютно твердого тела Различают 5 видов движения абсолютно твердого тела: поступательное движение; вращение вокруг
- 43. Поступательное движение абсолютно твердого тела При поступательном движении любая прямая, жестко связанная с движущимся телом, остается
- 44. Вращение абсолютно твердого тела вокруг неподвижной оси Вращением вокруг неподвижной оси называется движение, при котором существуют
- 45. Плоское движение абсолютно твердого тела При плоском движении траектория каждой точки твердого тела расположена в некоторой
- 46. Вращение абсолютно твердого тела вокруг неподвижной точки Вращение вокруг неподвижной точки называется движение твердого тела, имеющего
- 47. Свободное движение абсолютно твердого тела При свободном движении никаких кинематических ограничений на движение твердого тела не
- 48. Число степеней свободы Число степеней свободы тела – это количество независимых переменных (величин), которые необходимо задать,
- 49. ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ 1.5 Вращение твердого тела вокруг неподвижной оси
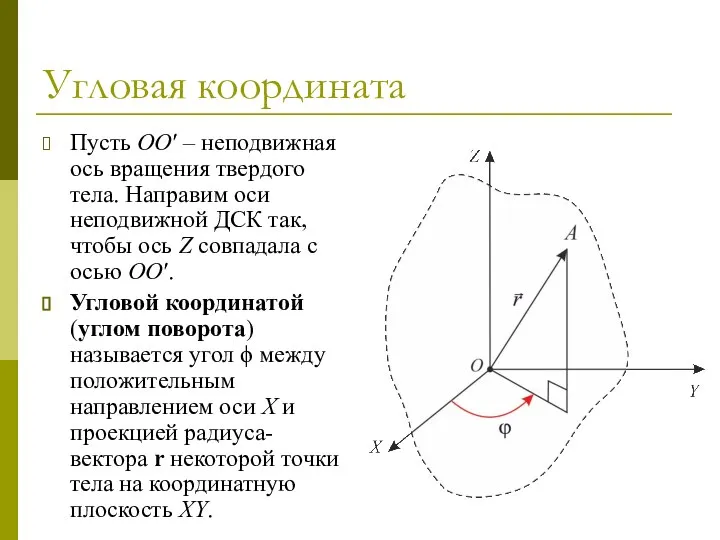
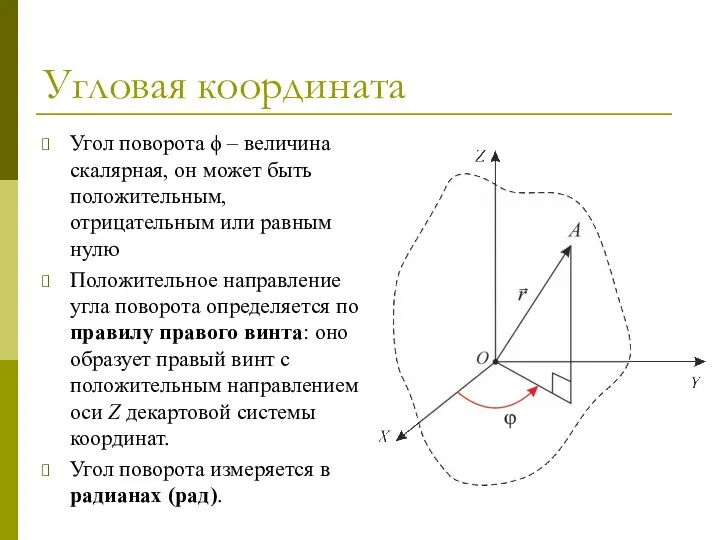
- 50. Угловая координата Пусть OO′ – неподвижная ось вращения твердого тела. Направим оси неподвижной ДСК так, чтобы
- 51. Угловая координата Угол поворота ϕ – величина скалярная, он может быть положительным, отрицательным или равным нулю
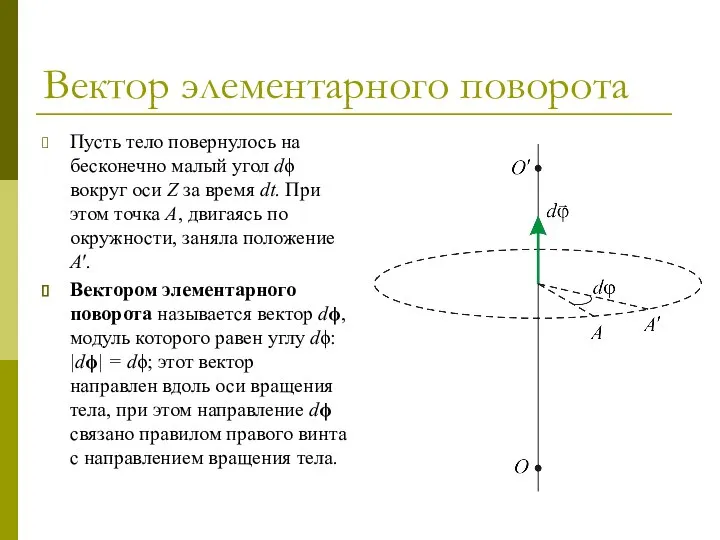
- 52. Вектор элементарного поворота Пусть тело повернулось на бесконечно малый угол dϕ вокруг оси Z за время
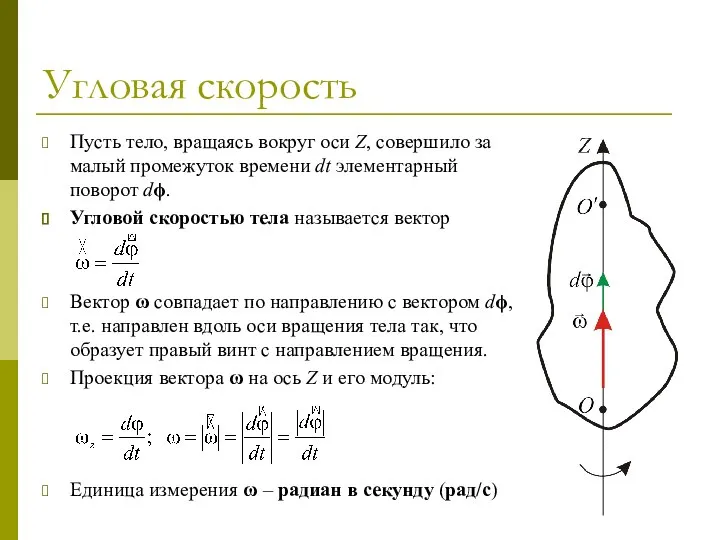
- 53. Угловая скорость Пусть тело, вращаясь вокруг оси Z, совершило за малый промежуток времени dt элементарный поворот
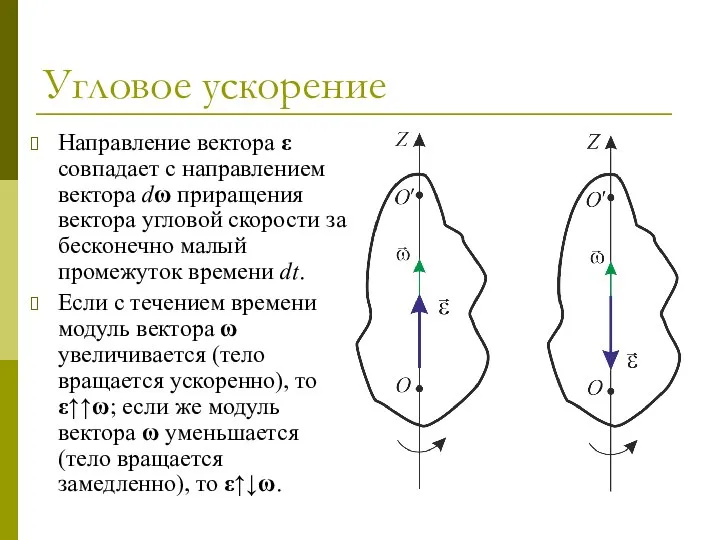
- 54. Угловое ускорение Угловым ускорением называется вектор, равный производной угловой скорости тела по времени: Проекция вектора углового
- 55. Угловое ускорение Направление вектора ε совпадает с направлением вектора dω приращения вектора угловой скорости за бесконечно
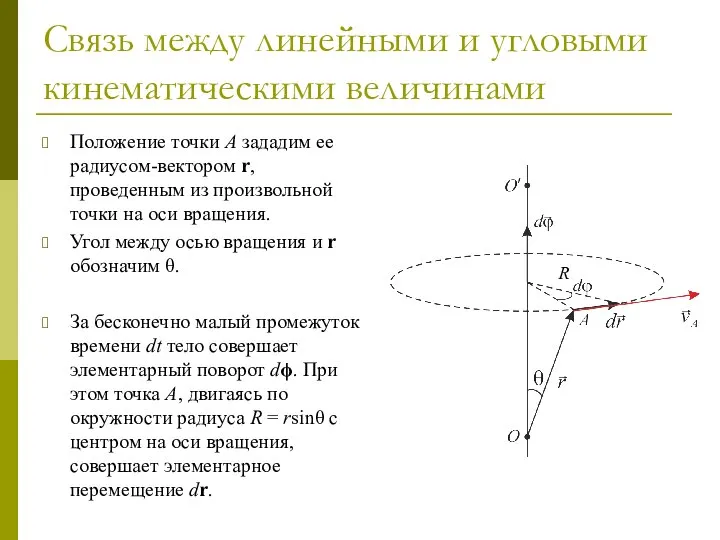
- 56. Связь между линейными и угловыми кинематическими величинами Постановка задачи. Пусть твердое тело вращается вокруг неподвижной оси
- 57. Связь между линейными и угловыми кинематическими величинами Положение точки A зададим ее радиусом-вектором r, проведенным из
- 58. Линейная скорость точки АТТ Модуль элементарного перемещения точки A: или в векторной форме: Тогда скорость точки
- 59. Угловое ускорение точки АТТ Найдем теперь выражение для ускорения точки A. Согласно определению ускорения, Первое слагаемое
- 60. Угловое ускорение точки АТТ Таким образом, полное ускорение точки A твердого тела:
- 61. ГЛАВА 1 ОСНОВЫ КИНЕМАТИКИ 1.6 Плоское движение твердого тела
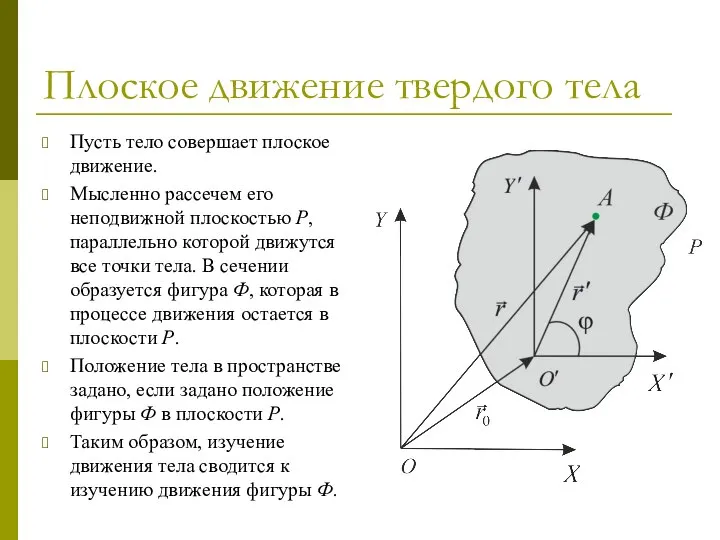
- 62. Плоское движение твердого тела Пусть тело совершает плоское движение. Мысленно рассечем его неподвижной плоскостью P, параллельно
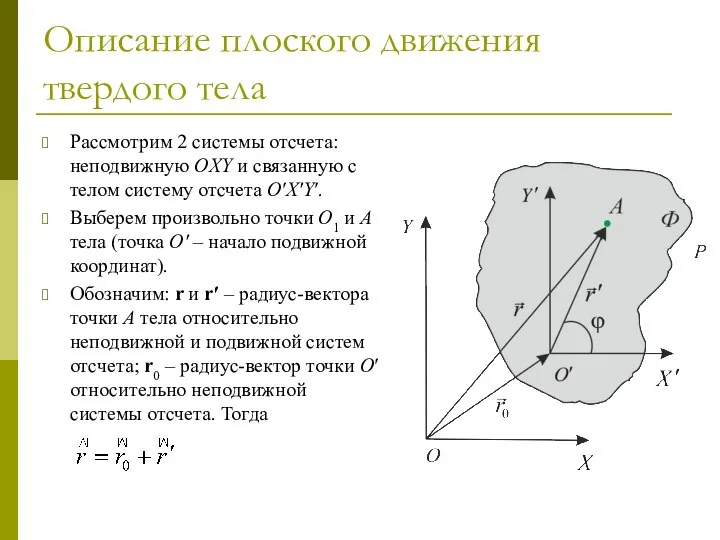
- 63. Описание плоского движения твердого тела Рассмотрим 2 системы отсчета: неподвижную OXY и связанную с телом систему
- 64. Линейная скорость точки твердого тела при его плоском движении Дифференцируем последнее равенство по времени, получаем: Здесь
- 65. Мгновенная ось вращения Таким образом, плоское движение твердого тела представляет собой совокупность 2-х видов движения –
- 67. Скачать презентацию













































 Синтез цифрового регулятора асинхронного електропривода в MATLAB
Синтез цифрового регулятора асинхронного електропривода в MATLAB Основы объективно-ориентированного программирования в среде Lazarus . Lazarus циклы
Основы объективно-ориентированного программирования в среде Lazarus . Lazarus циклы Геометрические тела
Геометрические тела Какую игрушку называют народной
Какую игрушку называют народной Критерии эффективности управленческого решения
Критерии эффективности управленческого решения Сборно-разборная эстакада
Сборно-разборная эстакада  Международная миграция рабочей силы
Международная миграция рабочей силы  Барокко 11 класс - Презентация_
Барокко 11 класс - Презентация_ Город мастеров Узюкино
Город мастеров Узюкино Бактерии
Бактерии Как узнать буквы корня в н_д
Как узнать буквы корня в н_д царство животных - презентация для начальной школы_
царство животных - презентация для начальной школы_ 6 grudnia Mikołaja
6 grudnia Mikołaja Северокавказский народ чеченцы
Северокавказский народ чеченцы Презентация на тему "23 февраля!" - скачать презентации по Педагогике
Презентация на тему "23 февраля!" - скачать презентации по Педагогике Концепция обучения русскому языку в старших классах: МОУ «Красноярская СОШ №1» Малахова Елена Васильевна
Концепция обучения русскому языку в старших классах: МОУ «Красноярская СОШ №1» Малахова Елена Васильевна Основы методики самостоятельных занятий физическими упражнениями. Самоконтроль при занятиях физической культурой и спортом
Основы методики самостоятельных занятий физическими упражнениями. Самоконтроль при занятиях физической культурой и спортом Презентация "Влияние античной культуры на современную жизнь" - скачать презентации по МХК
Презентация "Влияние античной культуры на современную жизнь" - скачать презентации по МХК Эластичность для менеджеров
Эластичность для менеджеров Сети связи и системы коммутации
Сети связи и системы коммутации Гражданское право
Гражданское право Характеристика основных моделей организационных культур
Характеристика основных моделей организационных культур Тестовые задания по ПДД.
Тестовые задания по ПДД. Emercom of Future. Молодежный форум робототехники МЧС. Проект "Роботы МЧС"
Emercom of Future. Молодежный форум робототехники МЧС. Проект "Роботы МЧС" Презентация "Эжен Делакруа" - скачать презентации по МХК
Презентация "Эжен Делакруа" - скачать презентации по МХК Международные индексы и рейтинги, структура и содержание
Международные индексы и рейтинги, структура и содержание мультипликатор цена/дивиденды в оценке стоимости предприятия
мультипликатор цена/дивиденды в оценке стоимости предприятия Азбука без букв (правила дорожного движения) Учитель 1-4 классов МБОУ «Кугесьский лицей» Чебоксарского района Чувашской Респу
Азбука без букв (правила дорожного движения) Учитель 1-4 классов МБОУ «Кугесьский лицей» Чебоксарского района Чувашской Респу