Содержание
- 2. Комбинаторные алгоритмы Исследуемые объекты представлены дискретными математическими структурами (множествами, графами). Требуется найти ответ на вопросы типа:
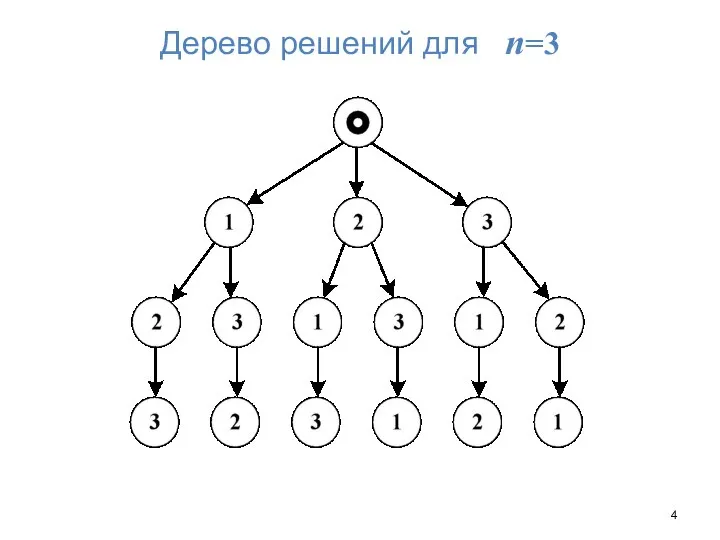
- 3. Перестановки Пример комбинаторной задачи: нахождение всех перестановок натуральных чисел от 1 до n: 1) первое число
- 4. Дерево решений для n=3
- 5. Перестановки
- 6. Алгоритм генерации всех перестановок В алгоритме используются 2 массива (их проще сделать глобальными, чтобы постоянно не
- 7. Алгоритм генерации всех перестановок void permut(int k) { for (int i = 0; i if (!Inc[i])
- 8. Сочетания
- 9. Алгоритм генерации всех сочетаний void combinat(int k) { int i = (!k)? 0 : Comb[k-1]+1; for
- 10. Задача о ферзях Пример для доски 4x4
- 11. Задача о ферзях Основные требования при поиске решения любой комбинаторной задачи: найти удобную форму для представления
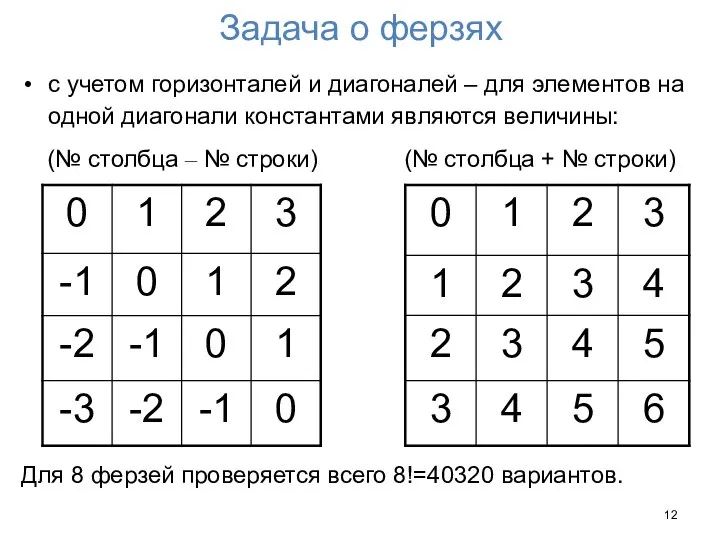
- 12. Задача о ферзях с учетом горизонталей и диагоналей – для элементов на одной диагонали константами являются
- 13. Гамильтоновы циклы и пути Гамильтонов цикл в неориентированном графе: начинается в произвольной вершине a проходит по
- 14. Гамильтоновы циклы и пути Любой гамильтонов цикл/путь задается некоторой перестановкой номеров вершин графа. Получать все перестановки,
- 15. Алгоритм поиска всех гамильтоновых циклов
- 16. Обертка для рекурсивной функции Для метода ham_loops необходимо заранее подготовить 2 массива и задать начальную вершину
- 17. Формализация комбинаторных задач
- 18. Бэктрекинг (поиск с возвратом)
- 19. Общий вид алгоритма поиска с возвратом Пусть S – текущее решение, M – множество элементов решений,
- 21. Скачать презентацию
















 Забота родителей и школы о здоровье младших подростков
Забота родителей и школы о здоровье младших подростков Управление e-learning проектом Тихомирова Елена Владимировна www.e-learningcenter.ru. - презентация
Управление e-learning проектом Тихомирова Елена Владимировна www.e-learningcenter.ru. - презентация Гостиничное дело. Основные службы гостиничного предприятия
Гостиничное дело. Основные службы гостиничного предприятия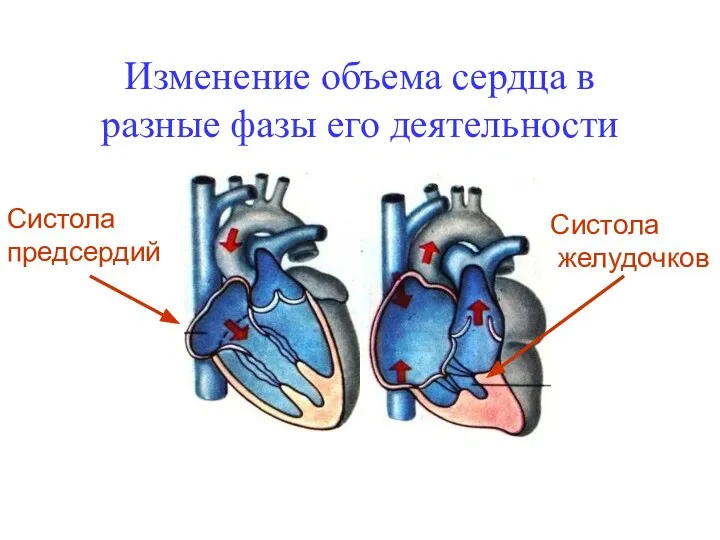 Изменение объема сердца в разные фазы его деятельности
Изменение объема сердца в разные фазы его деятельности Управление и организация монтажа холодильного оборудования в супермаркете
Управление и организация монтажа холодильного оборудования в супермаркете Основные направления в психологии
Основные направления в психологии Презентация "Проектирование системы управления предприятием" - скачать презентации по Экономике
Презентация "Проектирование системы управления предприятием" - скачать презентации по Экономике Народный праздник Масленица
Народный праздник Масленица Падежные окончания существительных
Падежные окончания существительных Презентация "Искусство" - скачать презентации по МХК
Презентация "Искусство" - скачать презентации по МХК Продажи гостиничного продукта на примере гостиницы «Центральная»
Продажи гостиничного продукта на примере гостиницы «Центральная» Модели каналов передачи данных
Модели каналов передачи данных Лечение о.аппендицита
Лечение о.аппендицита  Индивидуальные программы корпоративного страхования. - презентация
Индивидуальные программы корпоративного страхования. - презентация БЮДЖЕТИРОВАНИЕ ЗДРАВООХРАНЕНИЯ, ОРИЕНТИРОВАННОЕ НА РЕЗУЛЬТАТ доктор медицинских наук, профессор Флек Виталий Олегович
БЮДЖЕТИРОВАНИЕ ЗДРАВООХРАНЕНИЯ, ОРИЕНТИРОВАННОЕ НА РЕЗУЛЬТАТ доктор медицинских наук, профессор Флек Виталий Олегович Величаю Тебе, Боже, величаю
Величаю Тебе, Боже, величаю Принципы физического воспитания. Условия здорового образа жизни
Принципы физического воспитания. Условия здорового образа жизни Гражданское общество и правовое государство
Гражданское общество и правовое государство Элементы и соединения. Узлы Ферм. Лекция 9
Элементы и соединения. Узлы Ферм. Лекция 9 Юридические основы работы врача
Юридические основы работы врача 你知道四级的答题顺序吗
你知道四级的答题顺序吗 Знакомство с буквой З ,з Учитель: Пуговкина Елена Анатольевна Средняя общеобразовательная школа №7 города Ртищево Саратовской
Знакомство с буквой З ,з Учитель: Пуговкина Елена Анатольевна Средняя общеобразовательная школа №7 города Ртищево Саратовской  Лингво-стилистические особенности жанра: политическое аналитическое интервью
Лингво-стилистические особенности жанра: политическое аналитическое интервью Презентация на тему "ВМА - КТ в диагностике повреждений области лица" - скачать презентации по Медицине
Презентация на тему "ВМА - КТ в диагностике повреждений области лица" - скачать презентации по Медицине Алгоритмы и исполнители
Алгоритмы и исполнители Методика развития гибкости у детей 8-9 лет, занимающихся греко-римской борьбой
Методика развития гибкости у детей 8-9 лет, занимающихся греко-римской борьбой Монотипия – один из удивительных видов изобразительного искусства
Монотипия – один из удивительных видов изобразительного искусства Украшение и реальность. Паутинка. Изобразительная деятельность и художественный труд (2 класс)
Украшение и реальность. Паутинка. Изобразительная деятельность и художественный труд (2 класс)