Содержание
- 2. Systematic Changes in cj Objective function is replaced by Find the optimal solution as a function
- 3. Example: Wyndor Glass Problem Z(θ) = (3 + 2θ) x1+(5 - θ) x2
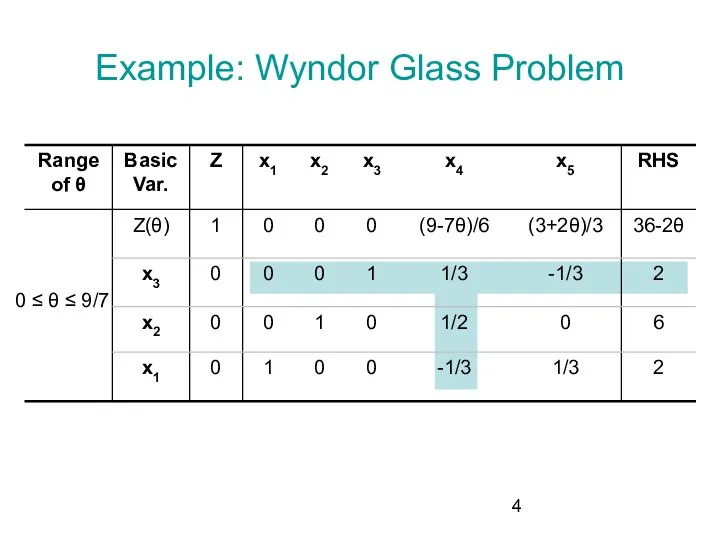
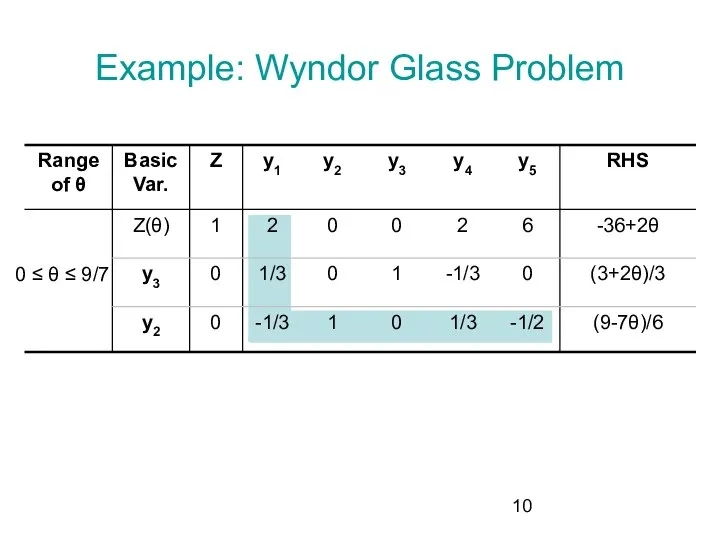
- 4. Example: Wyndor Glass Problem 0 ≤ θ ≤ 9/7
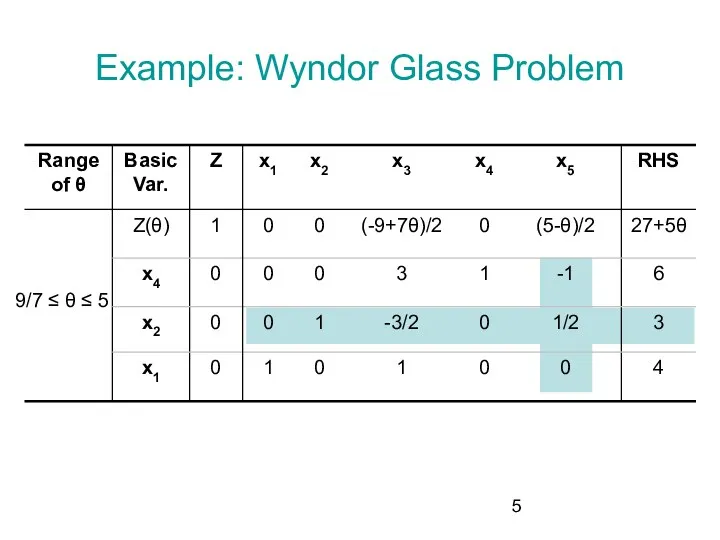
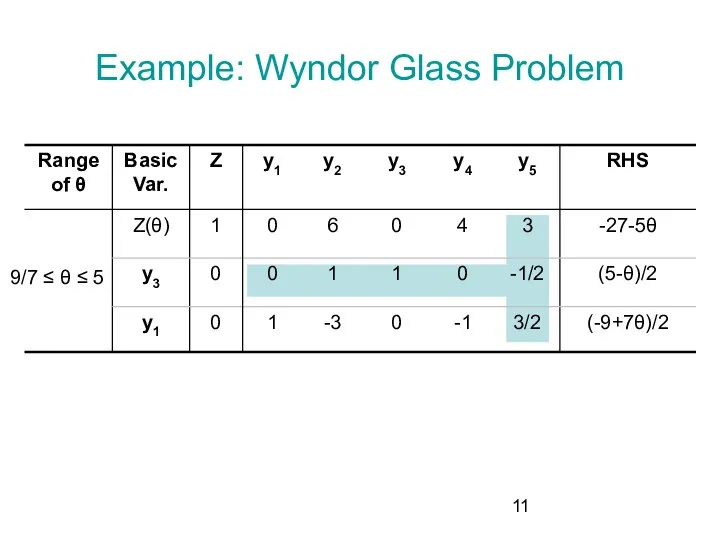
- 5. Example: Wyndor Glass Problem 9/7 ≤ θ ≤ 5
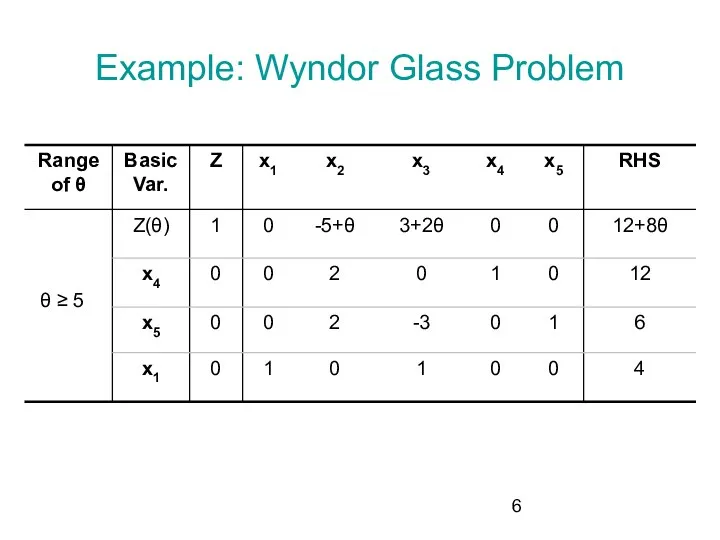
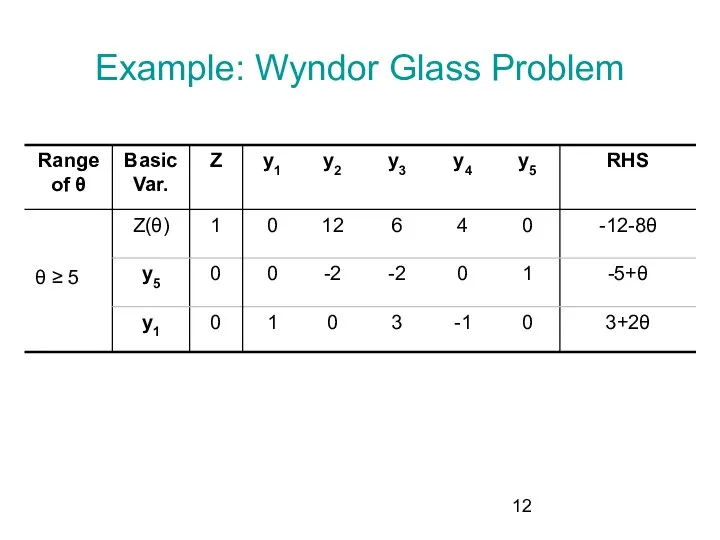
- 6. Example: Wyndor Glass Problem θ ≥ 5
- 7. Procedure Summary for Systematic Changes in cj 1. Solve the problem with θ = 0 by
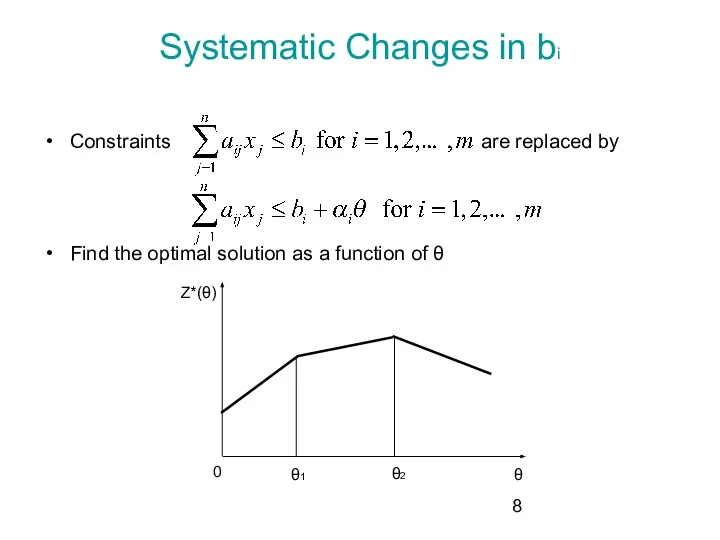
- 8. Systematic Changes in bi Constraints are replaced by Find the optimal solution as a function of
- 9. Example: Wyndor Glass Problem y1 + 3y3 ≥ 3 + 2θ 2y2 + 2y3 ≥ 5
- 10. Example: Wyndor Glass Problem 0 ≤ θ ≤ 9/7
- 11. Example: Wyndor Glass Problem 9/7 ≤ θ ≤ 5
- 12. Example: Wyndor Glass Problem θ ≥ 5
- 14. Скачать презентацию




 Экологические проблемы Урала
Экологические проблемы Урала  Аттестационная работа. Соперничество старого и нового света и его отражение в литературе
Аттестационная работа. Соперничество старого и нового света и его отражение в литературе УРОК ПО АЛГЕБРЕ 9 КЛАСС ТЕМА: СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ
УРОК ПО АЛГЕБРЕ 9 КЛАСС ТЕМА: СТЕПЕНЬ С ЦЕЛЫМ ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ  Easy access to embedded at SIM800(R)
Easy access to embedded at SIM800(R) Постуральный менеджмент. «Здоровое детство»
Постуральный менеджмент. «Здоровое детство» Презентация Налогообложение операций с ценными бумагами
Презентация Налогообложение операций с ценными бумагами Политический режим. Демократия
Политический режим. Демократия Многогранники геометрия 10-11 класс
Многогранники геометрия 10-11 класс Презентация на тему Молекулярные процессы синтеза у растений
Презентация на тему Молекулярные процессы синтеза у растений Мехатронные модули движения
Мехатронные модули движения Международное уголовное право
Международное уголовное право Политическая сфера
Политическая сфера Дарган мез
Дарган мез рисуем мальчика - презентация для начальной школы
рисуем мальчика - презентация для начальной школы Соединения. Классификация
Соединения. Классификация Федеральные государственные образовательные стандарты
Федеральные государственные образовательные стандарты  Антропогенное химическое загрязнение природной среды
Антропогенное химическое загрязнение природной среды Спортивная тренировка
Спортивная тренировка  Творчий проект «Переборні задачі Паскаль»
Творчий проект «Переборні задачі Паскаль» Презентация
Презентация Сельское хозяйство в России
Сельское хозяйство в России Презентация на тему: Жанры изобразительного искусства
Презентация на тему: Жанры изобразительного искусства буква с - презентация для начальной школы
буква с - презентация для начальной школы Мир византийской культуры Преподаватель истории Косарева Ирина Александровна МОУ Дивеевская СОШ С. Дивеево Нижегородской обла
Мир византийской культуры Преподаватель истории Косарева Ирина Александровна МОУ Дивеевская СОШ С. Дивеево Нижегородской обла Детско-юношеский отдых в регионах Татарстана. Лениногорский район
Детско-юношеский отдых в регионах Татарстана. Лениногорский район MICHELANGELO da CARAVAGGIO (1573-1610)
MICHELANGELO da CARAVAGGIO (1573-1610)  Древние образы, единство формы и декора в народных игрушках. Роспись дымковской игрушки
Древние образы, единство формы и декора в народных игрушках. Роспись дымковской игрушки Новосибирский государственный краеведческий музей
Новосибирский государственный краеведческий музей