Содержание
- 2. ГЕОГРАФИЧЕСКИЕ КАРТЫ Политическая Физическая карта карта Толчком, ускорившим развитие теории графов, явилась эпоха великих географических открытий.
- 3. ТЕОРЕМА О ЧЕТЫРЕХ КРАСКАХ. Теорема (доказана программистами IBM): Любую карту, нарисованную на плоскости или сфере, можно
- 4. ТОР Теорема 2: Любую карту, нарисованную на торе, можно раскрасить пятью красками так, что любые две
- 5. КРЕНДЕЛЬ Теорема 3: Любую карту, нарисованную на поверхности кренделя, можно раскрасить шестью красками так, что любые
- 6. ТОПОЛОГИЯ В топологии считается, что все тела сделаны из эластичного материала, и потому их можно сжимать
- 7. ОПРЕДЕЛЕНИЕ ПЛАНАРНОГО ГРАФА Граф, изображенный на плоскости или на шаре, называется плоским или планарным графом, если
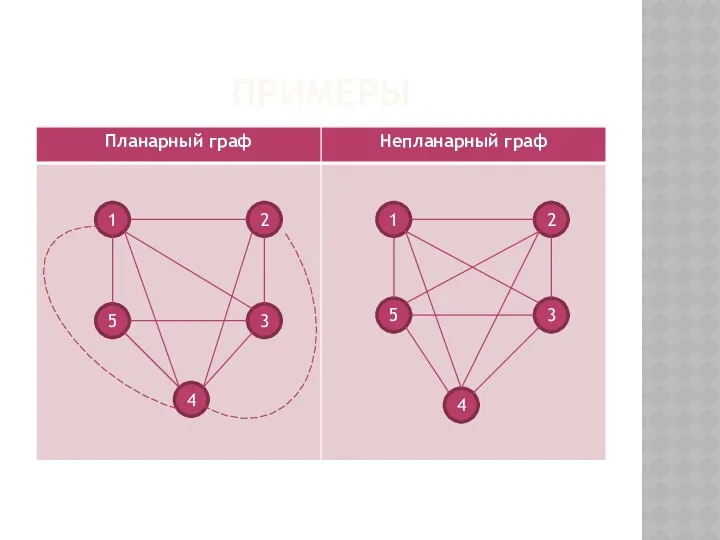
- 8. ПРИМЕРЫ 1 1 3 5 2 4 4 3 5 2
- 9. ЧТО ТАКОЕ «ГРАНЬ» Гранью (страной) в плоском представлении графа называется часть плоскости, ограниченная простым циклом и
- 10. ПРИМЕР
- 11. САМОСТОЯТЕЛЬНО Определить (занумеровать) все грани на планарном графе G(X,U): 1 5 3 6 2 4
- 12. ТЕОРЕМА ЭЙЛЕРА Пусть В - количество вершин в графе, Г - количество граней в плоском представлении
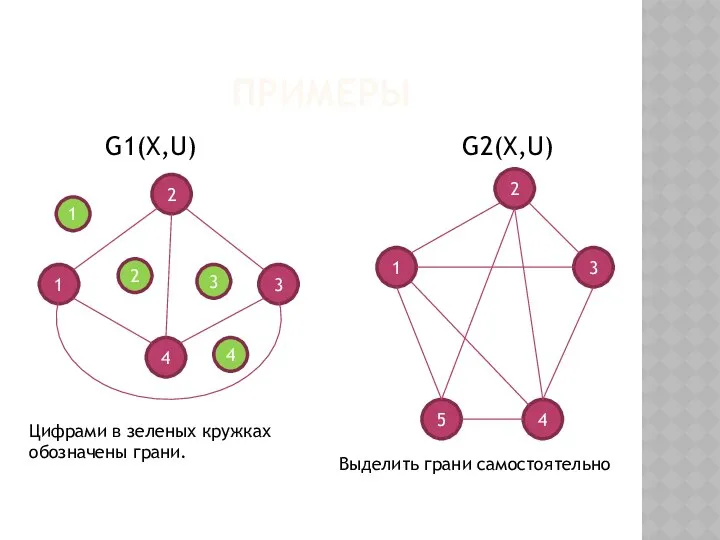
- 13. ПРИМЕРЫ G1(X,U) G2(X,U) 2 5 3 1 2 4 4 3 1 2 1 4 3
- 14. ФОРМУЛА ЭЙЛЕРА ДЛЯ НЕСВЯЗНОГО ГРАФА Для несвязного планарного графа с K компонентами связности формула Эйлера имеет
- 15. ПРИМЕР Несвязный планарный граф с К = 3 компонентами: 1 4 2 3 8 9 7
- 16. ТЕОРЕМА КУРАТОВСКОГО - ПОНТРЯГИНА Граф планарен тогда и только тогда, когда он не содержит подграфов типов,
- 17. САМОСТОЯТЕЛЬНО Проверить планарность графа G(X,U), изображенного ниже.
- 18. ДВОЙСТВЕННЫЕ ГРАФЫ Правила построения двойственного графа: 1. Каждая грань исходного графа заменяется вершиной двойственного. Если граф
- 19. ПРАВИЛО ПРАВОЙ РУКИ Построение двойственной дуги: 4 пальца указывают направление дуги исходного графа, а большой палец
- 20. ПРИМЕР Исходный орграф Двойственный орграф 2 4 3 1 1 2 3 1 2 3 Грани
- 21. СВОЙСТВА ДВОЙСТВЕННЫХ ГРАФОВ Простому контуру исходного графа, «закрученному» по часовой стрелке, соответствует вершина-источник двойственного графа. Простому
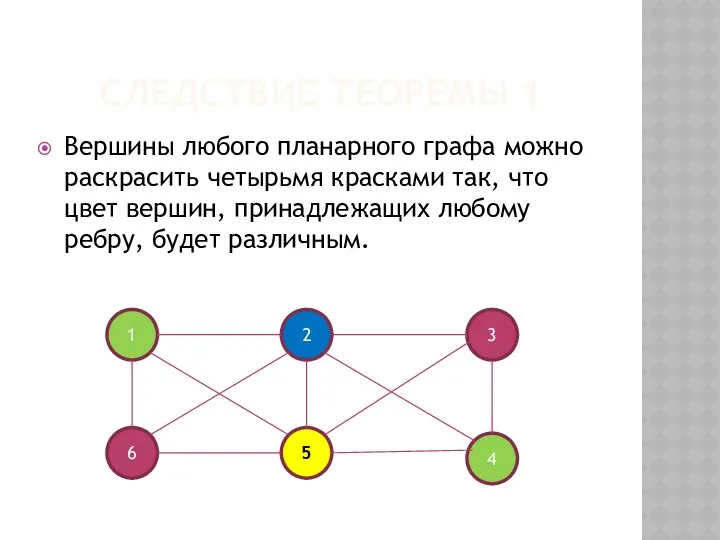
- 22. СЛЕДСТВИЕ ТЕОРЕМЫ 1 Вершины любого планарного графа можно раскрасить четырьмя красками так, что цвет вершин, принадлежащих
- 23. САМОСТОЯТЕЛЬНО Раскрасить вершины графа G(X,U) четырьмя красками так, чтобы цвет вершин, принадлежащих любому ребру, был различным.
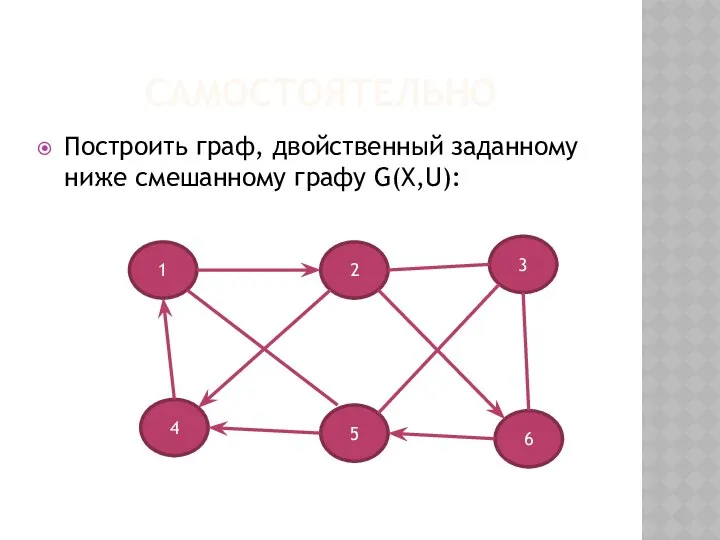
- 24. САМОСТОЯТЕЛЬНО Построить граф, двойственный заданному ниже смешанному графу G(X,U): 1 4 5 6 3 2
- 25. САМОСТОЯТЕЛЬНО Определить вес дуг и ребер графа, двойственного заданному ниже взвешенному смешанному графу G(X,U): 1 4
- 27. Скачать презентацию




















 Текст Государственного гимна Российской Федерации. Конституция Российской Федерации,
Текст Государственного гимна Российской Федерации. Конституция Российской Федерации, Организация работы на уроках русского языка с использованием ТУДО
Организация работы на уроках русского языка с использованием ТУДО Запорожские казаки сегодня
Запорожские казаки сегодня Социолингвистика в США
Социолингвистика в США Некоторые приемы работы со сборками. Анализ собираемости
Некоторые приемы работы со сборками. Анализ собираемости Тема: «Возрастная периодизация психического развития человека»
Тема: «Возрастная периодизация психического развития человека»  Подшипники скольжения
Подшипники скольжения Тема урока: Жизнь египетского вельможи План урока: В усадьбе вельможи Служба вельмож Вельможа при дворе фараона
Тема урока: Жизнь египетского вельможи План урока: В усадьбе вельможи Служба вельмож Вельможа при дворе фараона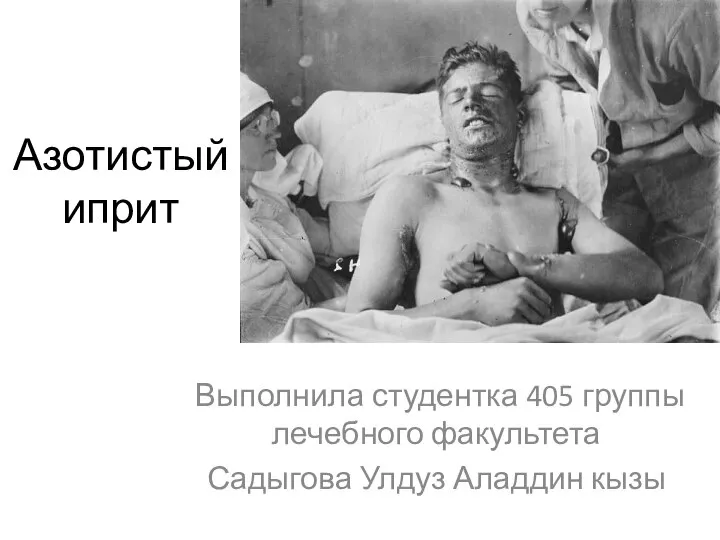 Азотистый иприт
Азотистый иприт  Закономерности распределения напряжений в грунте фазы деформаций грунта под фундаментом
Закономерности распределения напряжений в грунте фазы деформаций грунта под фундаментом Федеральный закон-52 О санитарно-эпидемиологическом благополучии населения
Федеральный закон-52 О санитарно-эпидемиологическом благополучии населения Презентация Рынок недвижимости и особенности его функционирования
Презентация Рынок недвижимости и особенности его функционирования  Приборы радиационного контроля
Приборы радиационного контроля  Разработка мехатронного модуля выдвижного устройства гидрологического прибора
Разработка мехатронного модуля выдвижного устройства гидрологического прибора МУЛЬТИПЛИКАТОР ЦЕНА/ВЫРУЧКА ОТ РЕАЛИЗАЦИИ В ОЦЕНКЕ СТОИМОСТИ ПРЕДПРИЯТИЯ (БИЗНЕСА)
МУЛЬТИПЛИКАТОР ЦЕНА/ВЫРУЧКА ОТ РЕАЛИЗАЦИИ В ОЦЕНКЕ СТОИМОСТИ ПРЕДПРИЯТИЯ (БИЗНЕСА)  Презентация Управление развитием таможенной деятельности в Стратегии развития таможенной службы
Презентация Управление развитием таможенной деятельности в Стратегии развития таможенной службы  Ферми-системы. Модель Хаббарда
Ферми-системы. Модель Хаббарда открывая двери_финал
открывая двери_финал Финансовое планирование и прогнозирование
Финансовое планирование и прогнозирование  Механический мерительный инструмент с преобразователями
Механический мерительный инструмент с преобразователями ВНЕШНЯЯ И ВНУТРЕННЯЯ СРЕДА ОРГАЗИЗАЦИИ
ВНЕШНЯЯ И ВНУТРЕННЯЯ СРЕДА ОРГАЗИЗАЦИИ Закон о кассовых аппаратах
Закон о кассовых аппаратах Назначение таможенной операции «временное хранение товаров» Презентацию подготовил студент 1 курса Фомин Максим
Назначение таможенной операции «временное хранение товаров» Презентацию подготовил студент 1 курса Фомин Максим  Презентация по экономике на тему: «История возникновения денег»
Презентация по экономике на тему: «История возникновения денег» Конденсаторы: виды, характеристики
Конденсаторы: виды, характеристики Специалист в автоматизации
Специалист в автоматизации Общие сведения о сборно-разборных и цельноперевозимых пролетных строениях
Общие сведения о сборно-разборных и цельноперевозимых пролетных строениях АНО ДОД ДЮСШ «REAL-M»
АНО ДОД ДЮСШ «REAL-M»