Содержание
- 2. Содержание 1. Основные понятия и определения 1.1. Уравнения и характеристики плоскопараллельного движения тела 1.2. Определение скоростей
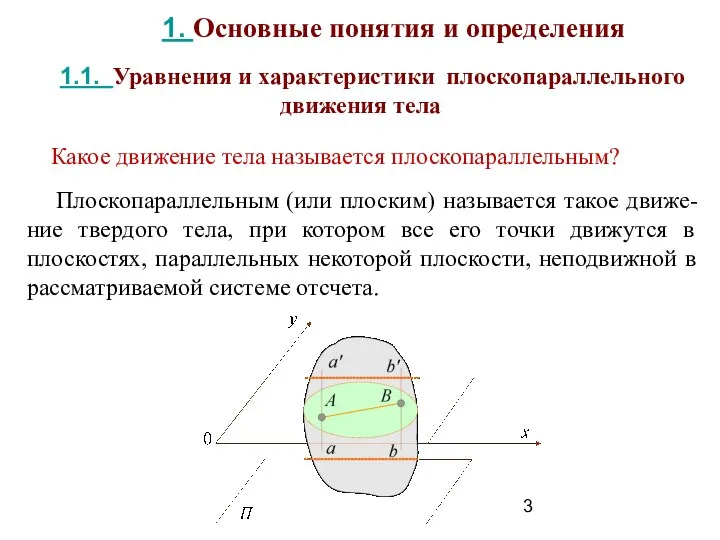
- 3. Плоскопараллельным (или плоским) называется такое движе-ние твердого тела, при котором все его точки движутся в плоскостях,
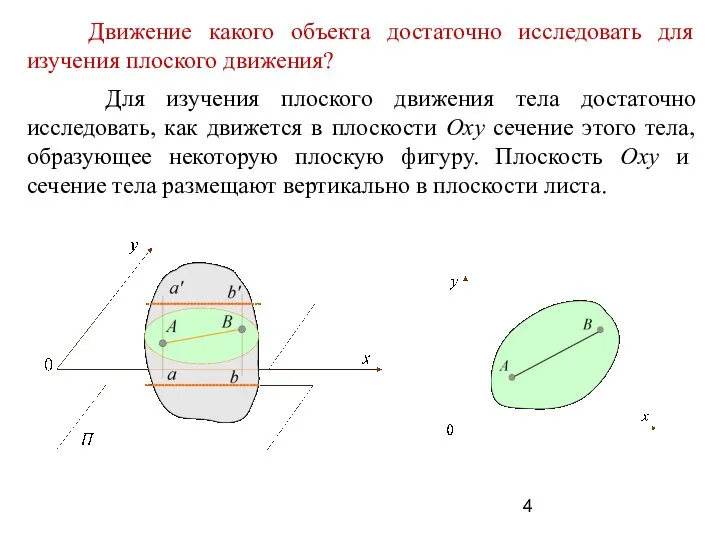
- 4. Для изучения плоского движения тела достаточно исследовать, как движется в плоскости Оху сечение этого тела, образующее
- 5. Чем определяется положение плоской фигуры при движении в плоскости Oxy? Положение плоской фигуры в плоскости Оху
- 6. Закон движения плоской фигуры в ее плоскости, а следова-тельно, и плоского движения твердого тела относительно системы
- 7. Назовите основные кинематические характеристики плоского движения тела? Какая точка выбирается за полюс? В качестве полюса вообще
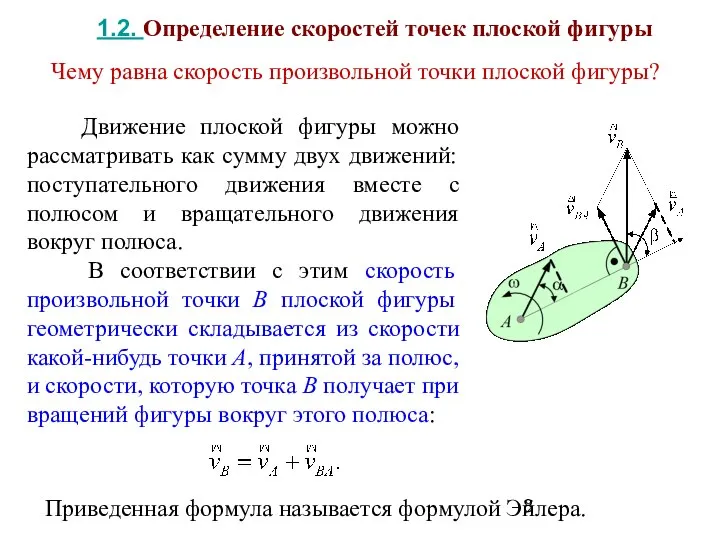
- 8. Движение плоской фигуры можно рассматривать как сумму двух движений: поступательного движения вместе с полюсом и вращательного
- 9. Чему равна скорость точки B во вращательном движении вокруг полюса? Как формулируется теорема о проекциях скоростей
- 10. Что называется мгновенным центром скоростей? Точка плоской фигуры, скорость которой в данный момент времени равна нулю,
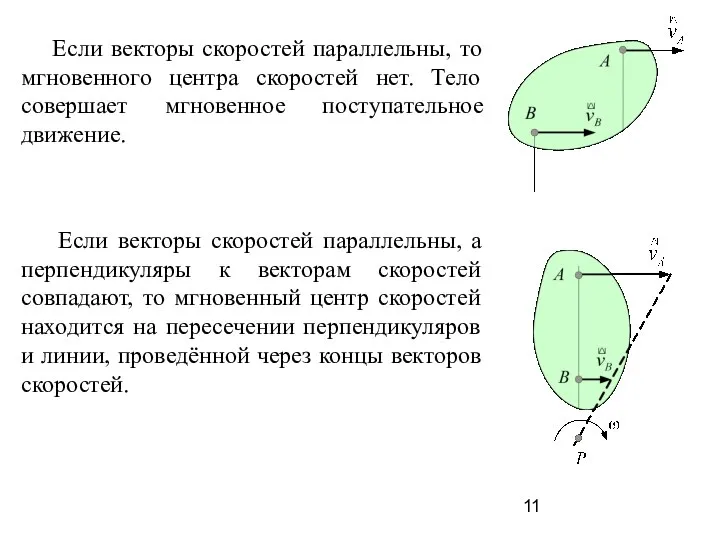
- 11. Если векторы скоростей параллельны, то мгновенного центра скоростей нет. Тело совершает мгновенное поступательное движение. Если векторы
- 12. Если векторы скоростей параллельны и противоположны, а перпендикуляры к векто-рам скоростей совпадают, то мгновенный центр скоростей
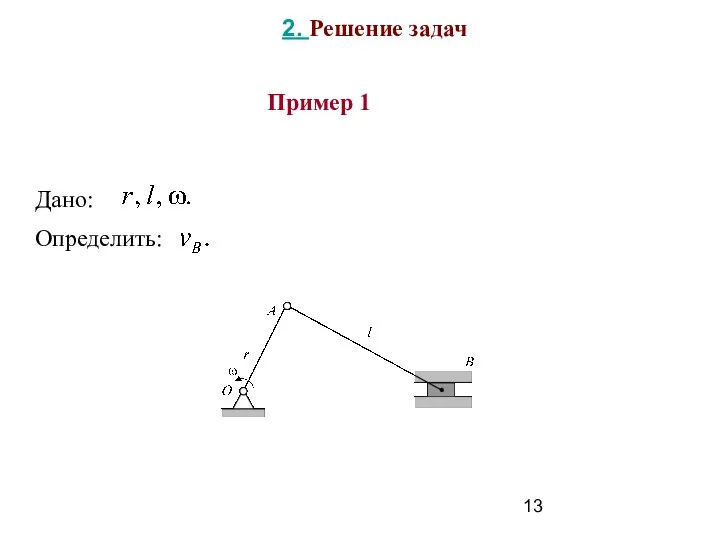
- 13. Пример 1 2. Решение задач
- 14. Решение (Применение формулы Эйлера) В кривошипно-шатунном механизме плоскопараллельное движение совершает шатун АВ. Примем точку А за
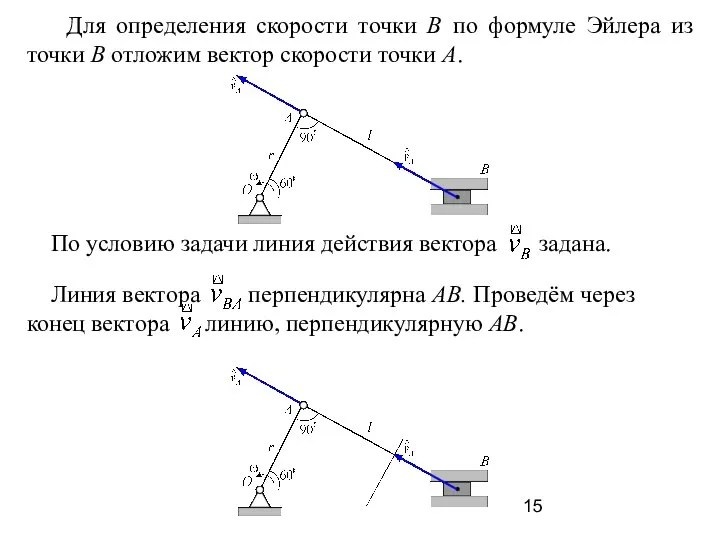
- 15. Для определения скорости точки В по формуле Эйлера из точки В отложим вектор скорости точки А.
- 16. Расставим стрелки векторов в соответствии с формулой Эйлера. Из векторного треугольника найдём скорость точки В.
- 17. Попутно можно из треугольника найти скорость точки В во вращательном движении вокруг полюса А.
- 18. Аналитический способ При аналитическом способе применения формулы Эйлера в точке В строятся векторы скоростей, линии действия
- 19. Из полученной системы уравнений находим неизвестные величины. Из второго уравнения: Подставляем vВА в первое уравнение и
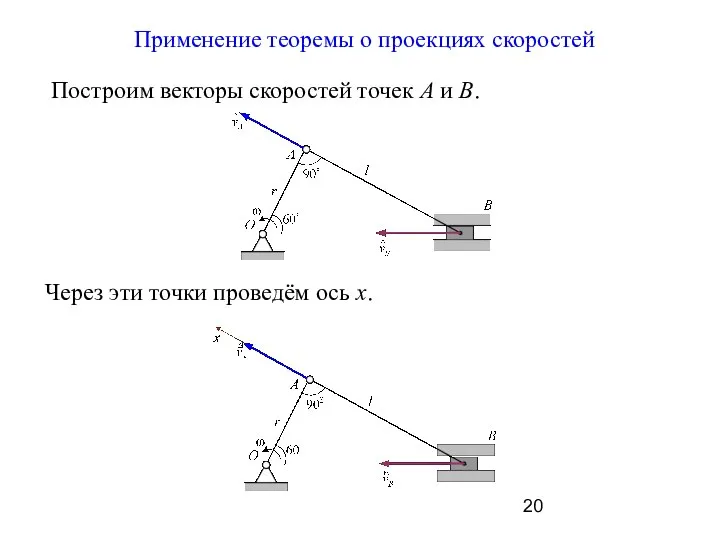
- 20. Применение теоремы о проекциях скоростей Построим векторы скоростей точек А и В. Через эти точки проведём
- 21. По теореме о проекциях скоростей двух точек плоской фигуры: Находим из рисунка проекции на ось x
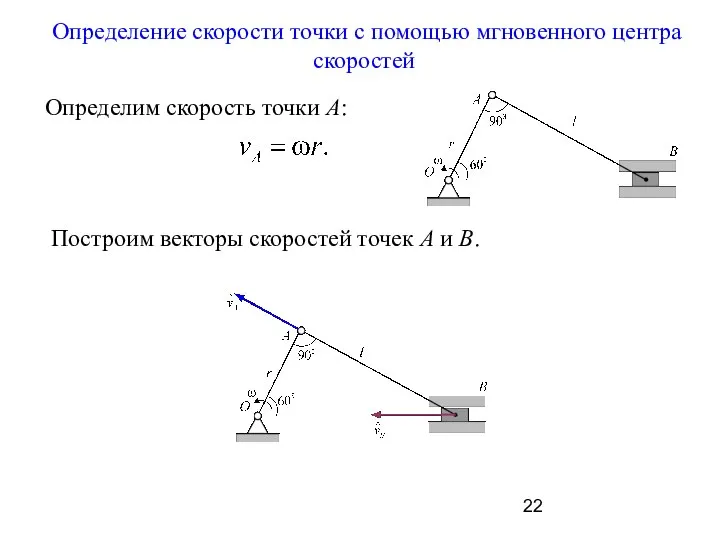
- 22. Определение скорости точки с помощью мгновенного центра скоростей Определим скорость точки А: Построим векторы скоростей точек
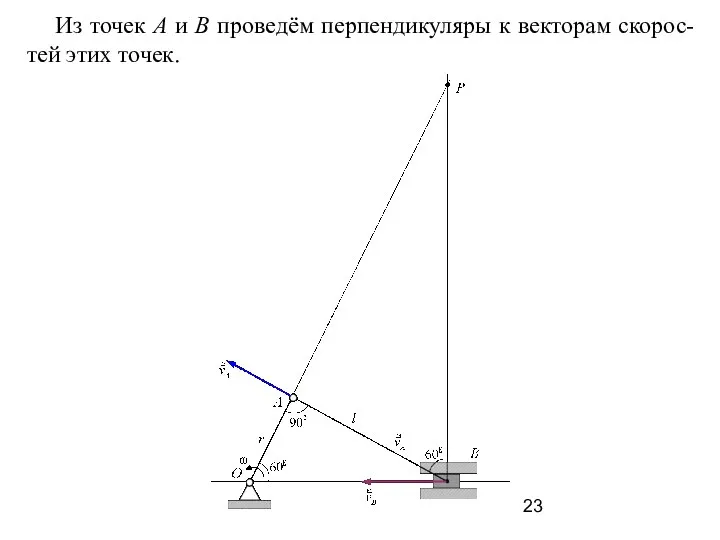
- 23. Из точек А и В проведём перпендикуляры к векторам скорос-тей этих точек.
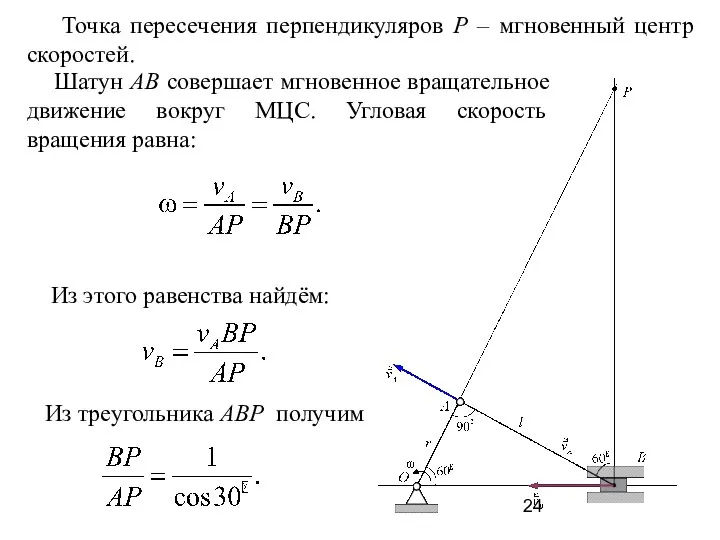
- 24. Точка пересечения перпендикуляров Р – мгновенный центр скоростей. Шатун АВ совершает мгновенное вращательное движение вокруг МЦС.
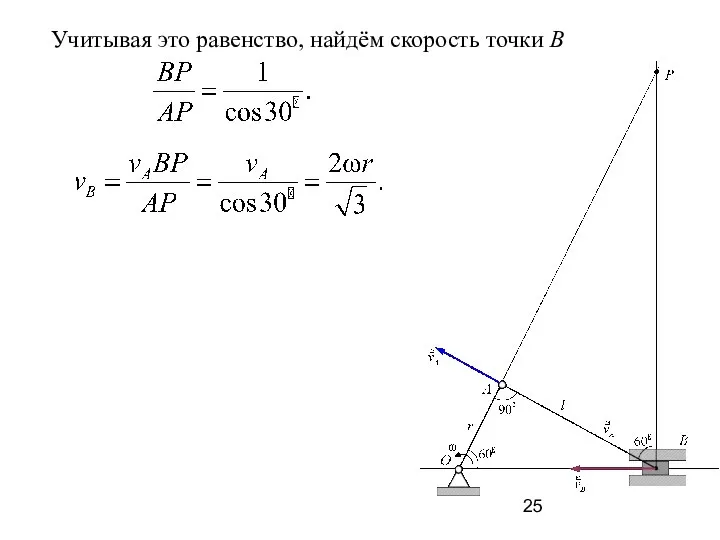
- 25. Учитывая это равенство, найдём скорость точки В
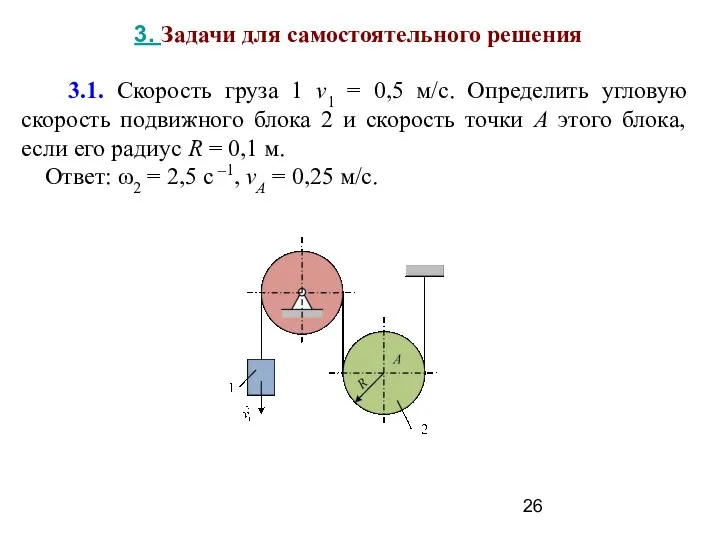
- 26. 3.1. Скорость груза 1 v1 = 0,5 м/с. Определить угловую скорость подвижного блока 2 и скорость
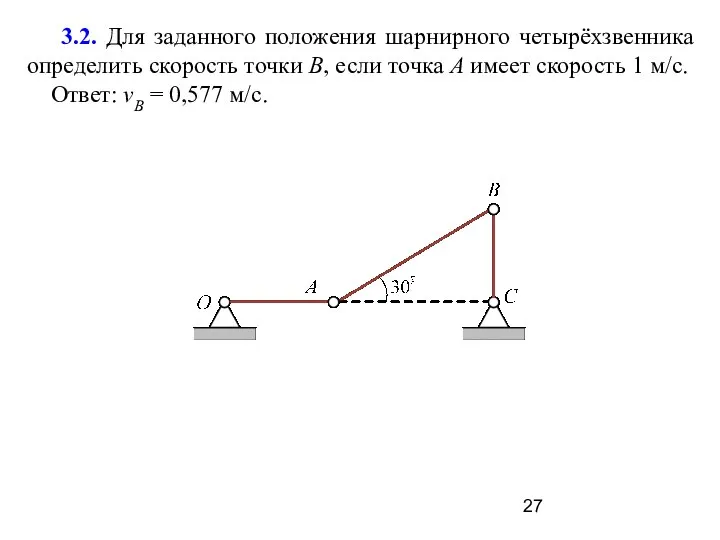
- 27. 3.2. Для заданного положения шарнирного четырёхзвенника определить скорость точки В, если точка А имеет скорость 1
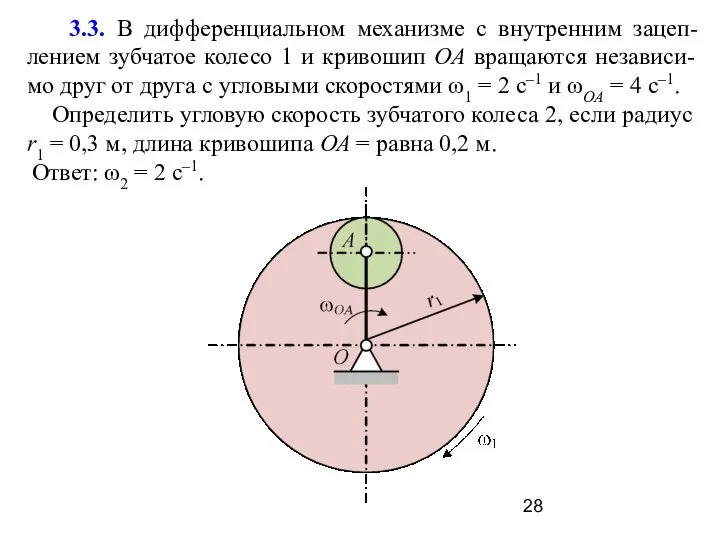
- 28. 3.3. В дифференциальном механизме с внутренним зацеп-лением зубчатое колесо 1 и кривошип ОА вращаются независи-мо друг
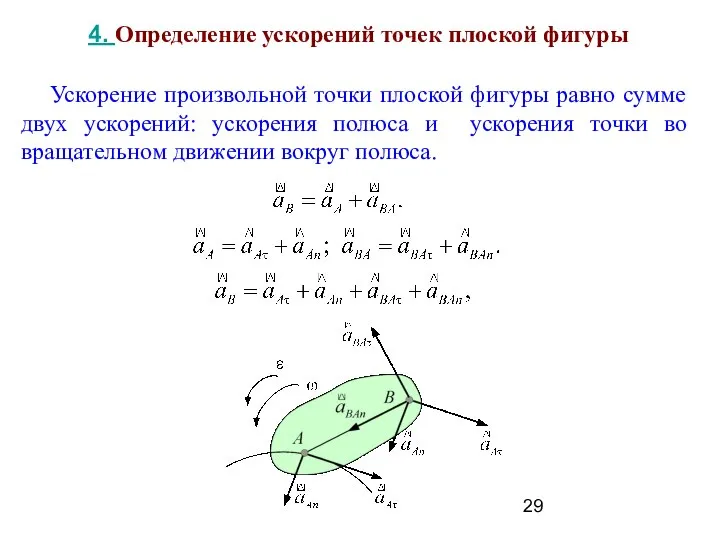
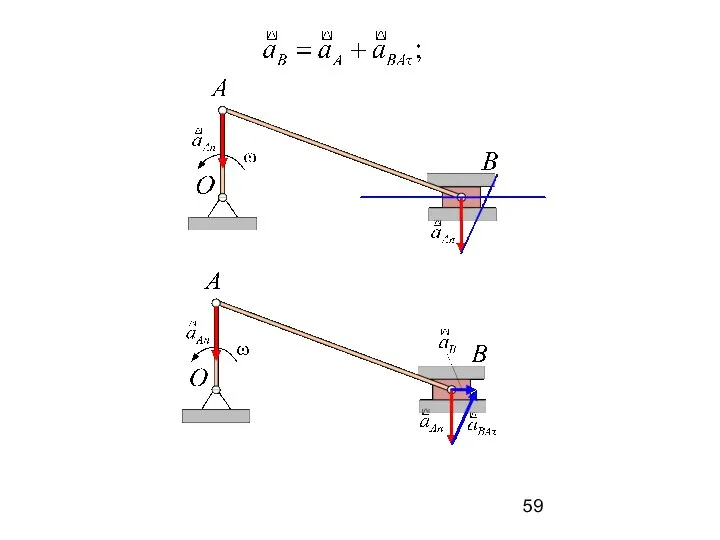
- 29. Ускорение произвольной точки плоской фигуры равно сумме двух ускорений: ускорения полюса и ускорения точки во вращательном
- 30. При решении задач векторное выражение ускорения точки плоской фигуры проецируется на координатные оси: Если неизвестным является
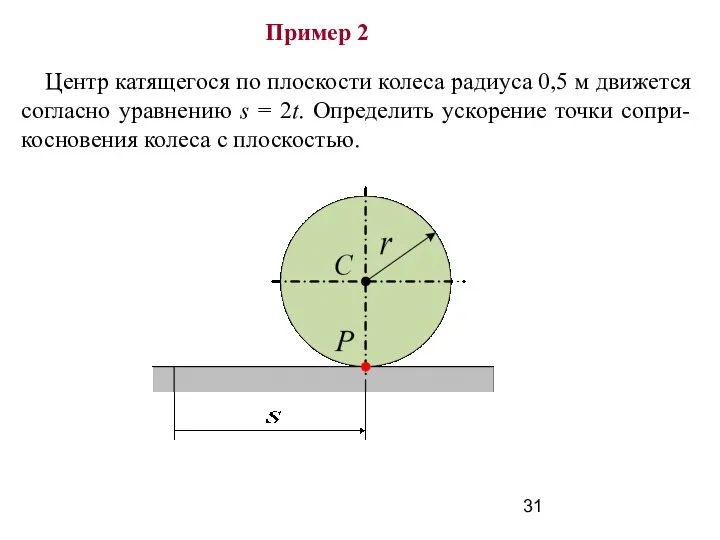
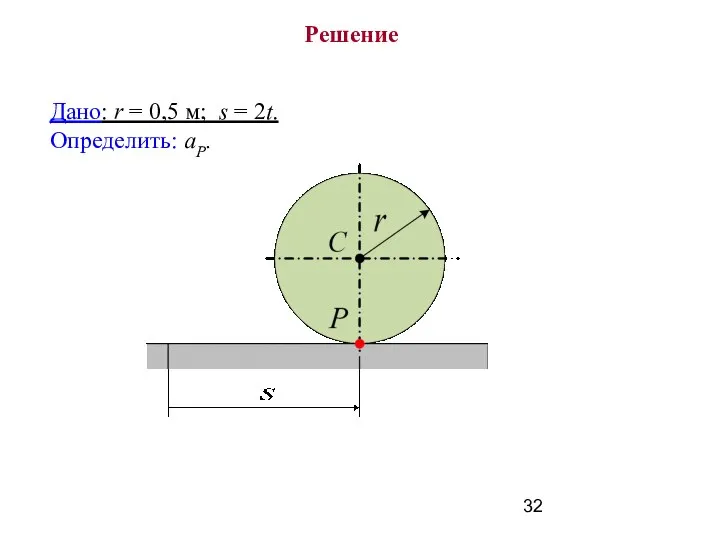
- 31. Пример 2 Центр катящегося по плоскости колеса радиуса 0,5 м движется согласно уравнению s = 2t.
- 32. Дано: r = 0,5 м; s = 2t. Определить: аР. Решение
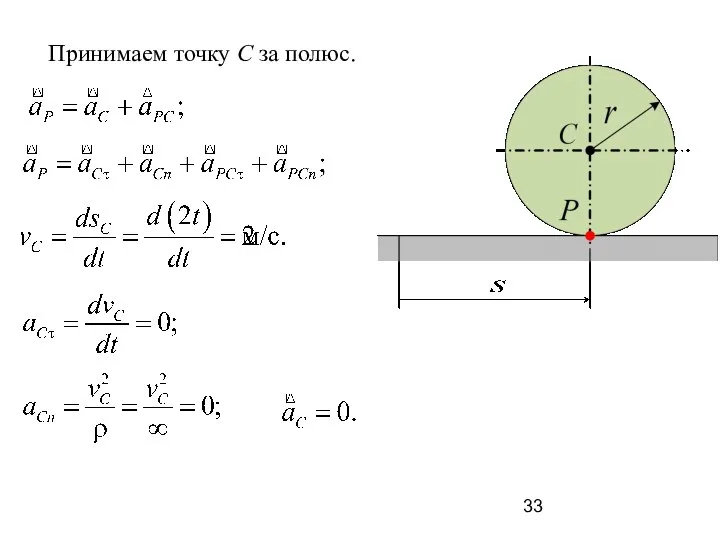
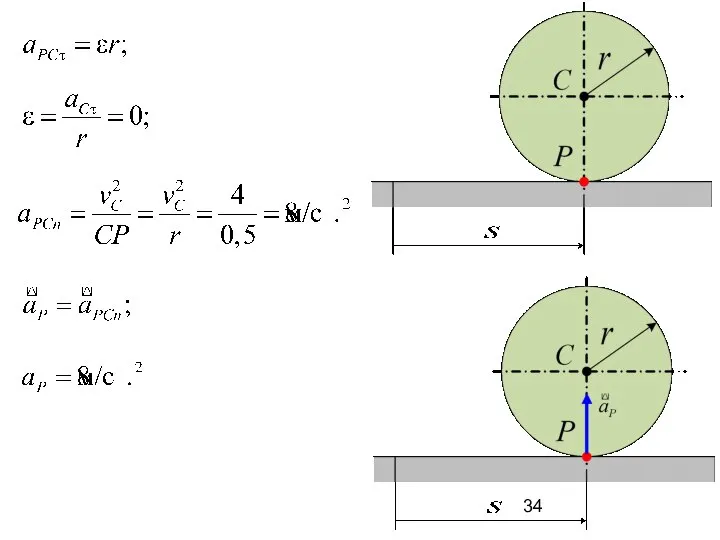
- 33. Принимаем точку С за полюс.
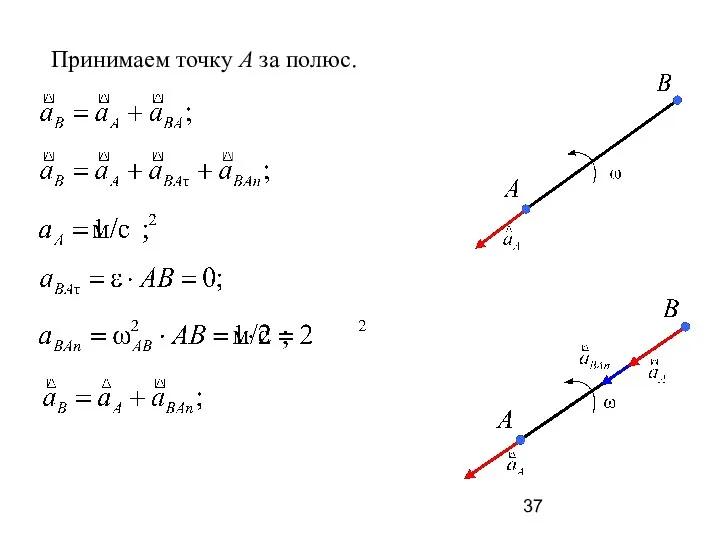
- 35. Пример 3 Стержень АВ длиной 2 м находится в плоскопараллельном движении. Найти ускорение точки В, если
- 36. Дано: АВ = 2 м; аА = 1 м/с2; ω = 1 рад/с; ε = 0.
- 37. Принимаем точку A за полюс.
- 38. Пример 4 Стержень АВ движется в плоскости. Ускорение точки А в данный момент времени аА =
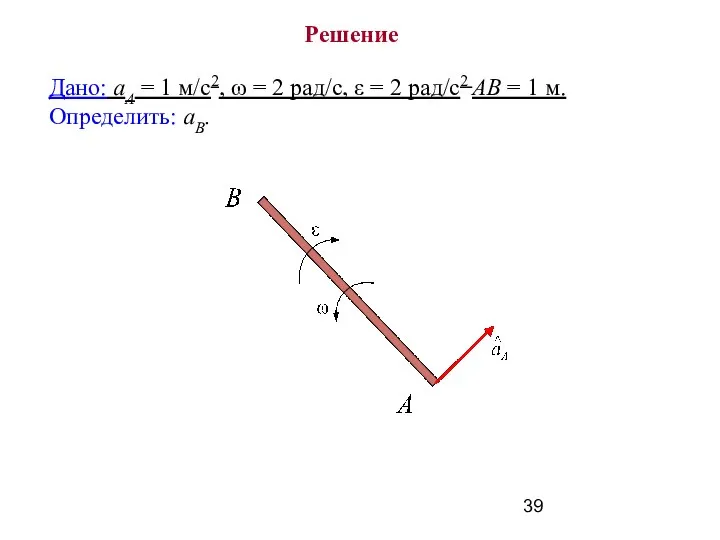
- 39. Дано: аА = 1 м/с2, ω = 2 рад/с, ε = 2 рад/c2 АВ = 1
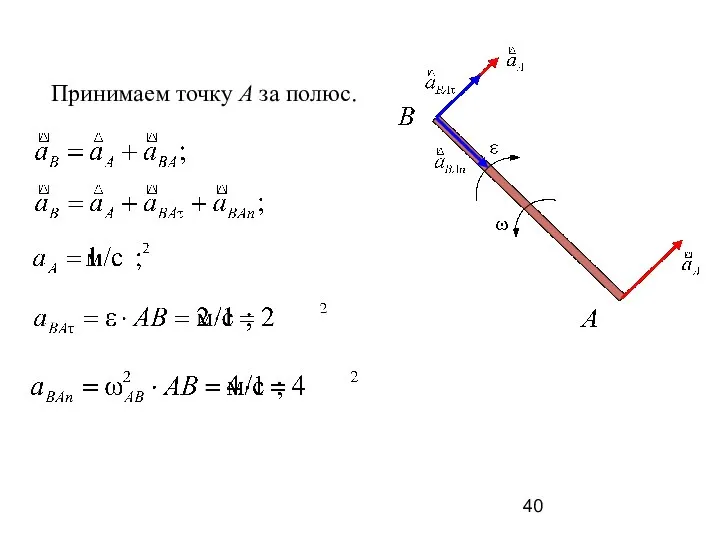
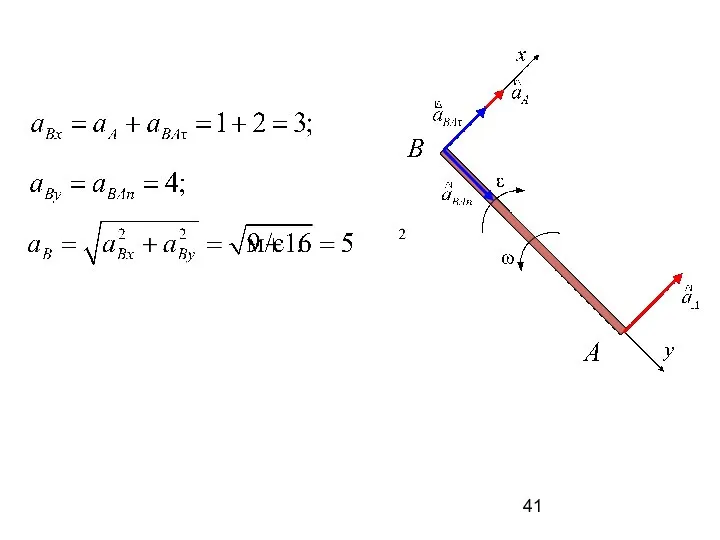
- 40. Принимаем точку A за полюс.
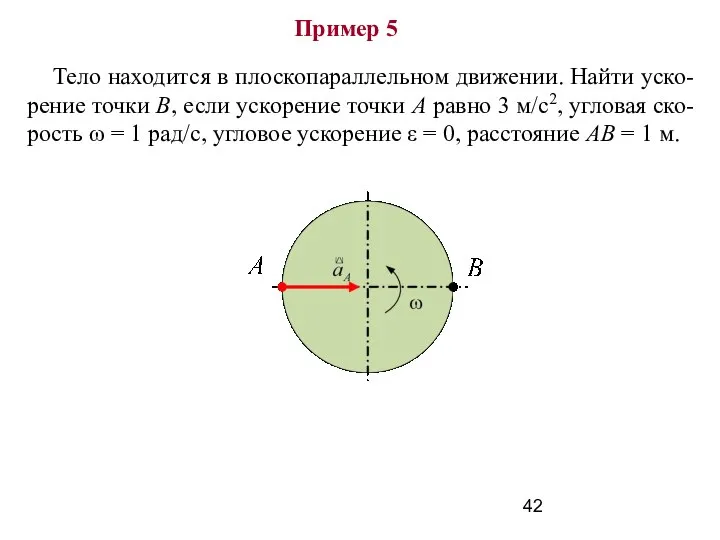
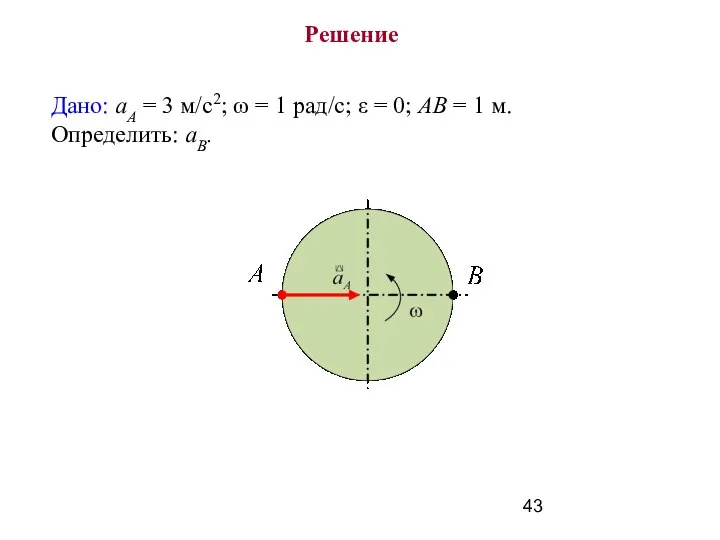
- 42. Пример 5 Тело находится в плоскопараллельном движении. Найти уско-рение точки В, если ускорение точки А равно
- 43. Дано: аА = 3 м/с2; ω = 1 рад/с; ε = 0; АВ = 1 м.
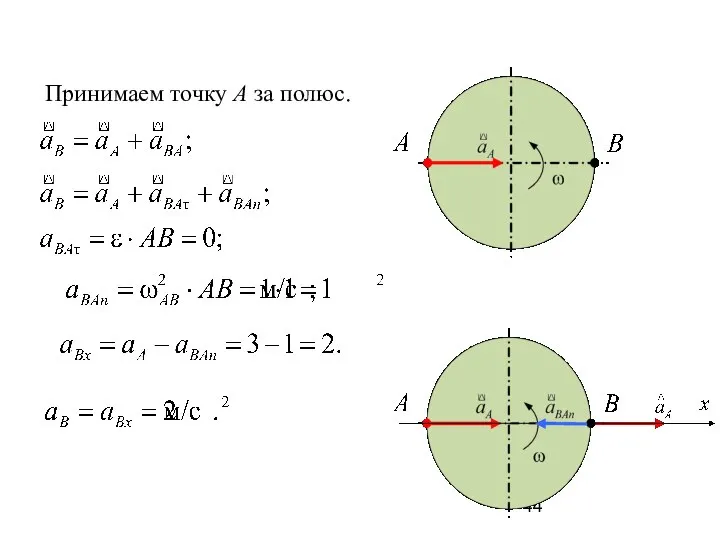
- 44. Принимаем точку A за полюс.
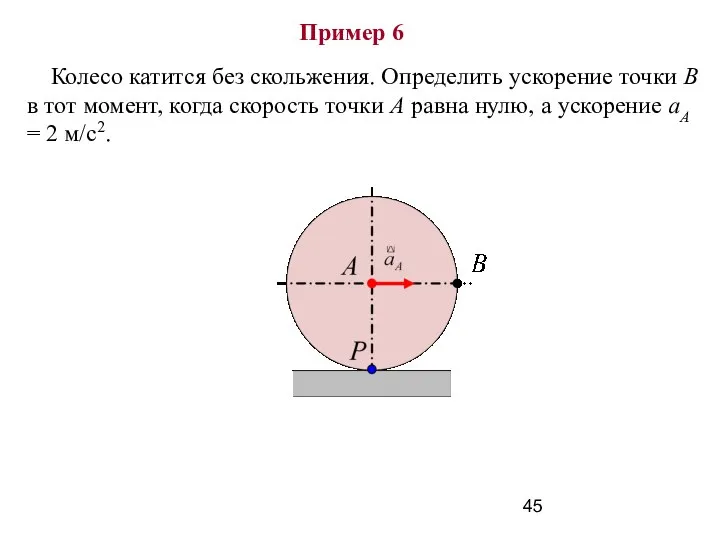
- 45. Пример 6 Колесо катится без скольжения. Определить ускорение точки В в тот момент, когда скорость точки
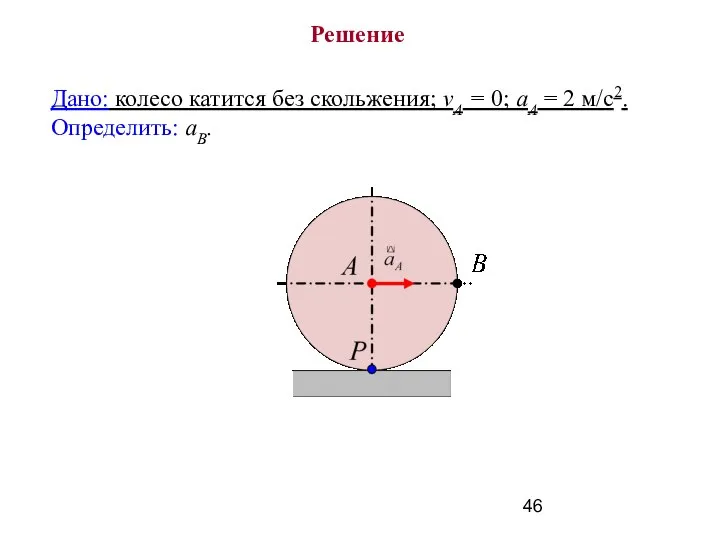
- 46. Дано: колесо катится без скольжения; vА = 0; аА = 2 м/с2. Определить: аВ. Решение
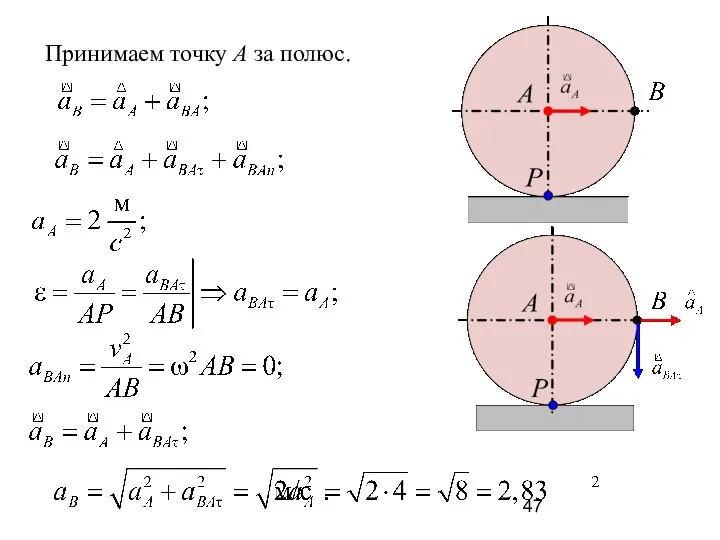
- 47. Принимаем точку A за полюс.
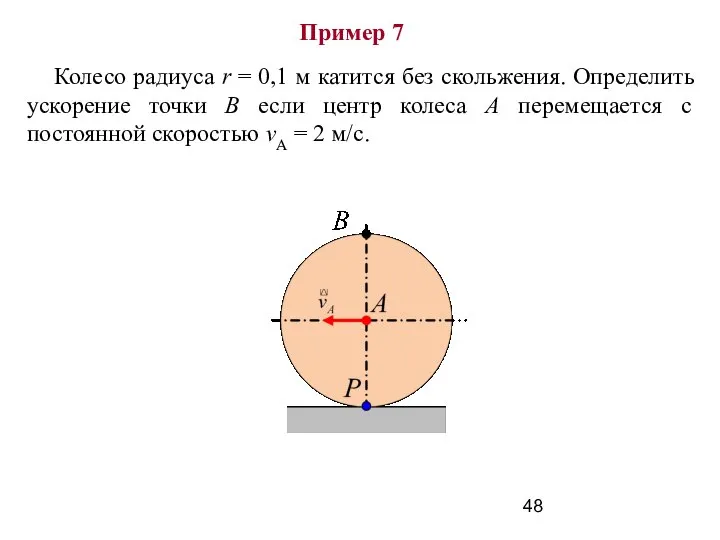
- 48. Пример 7 Колесо радиуса r = 0,1 м катится без скольжения. Определить ускорение точки В если
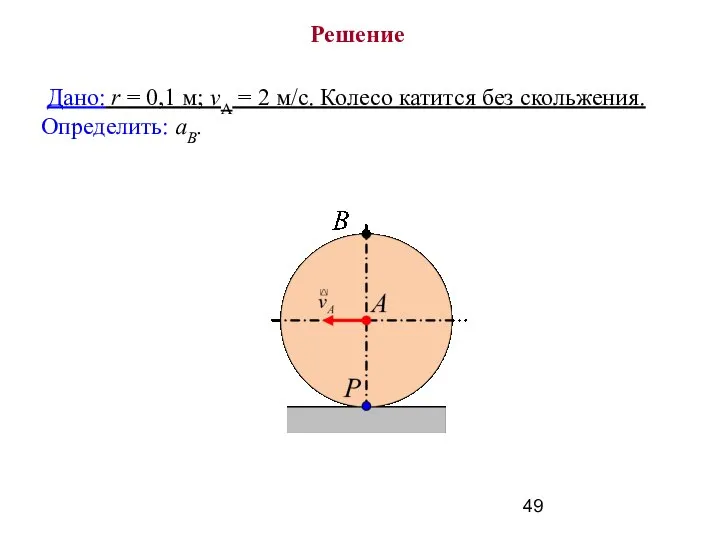
- 49. Решение Дано: r = 0,1 м; vА = 2 м/с. Колесо катится без скольжения. Определить: аВ.
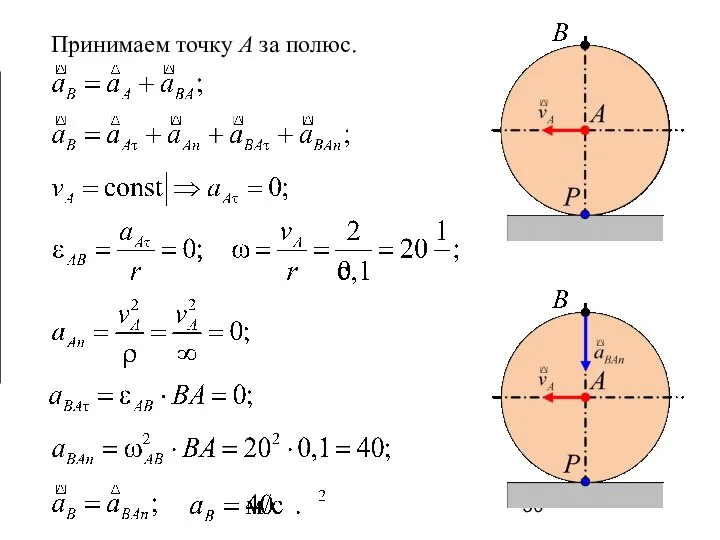
- 50. Принимаем точку A за полюс.
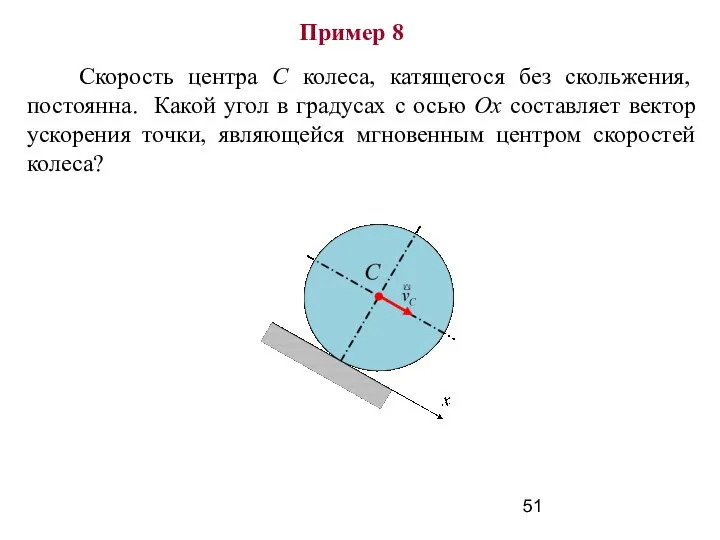
- 51. Пример 8 Скорость центра С колеса, катящегося без скольжения, постоянна. Какой угол в градусах с осью
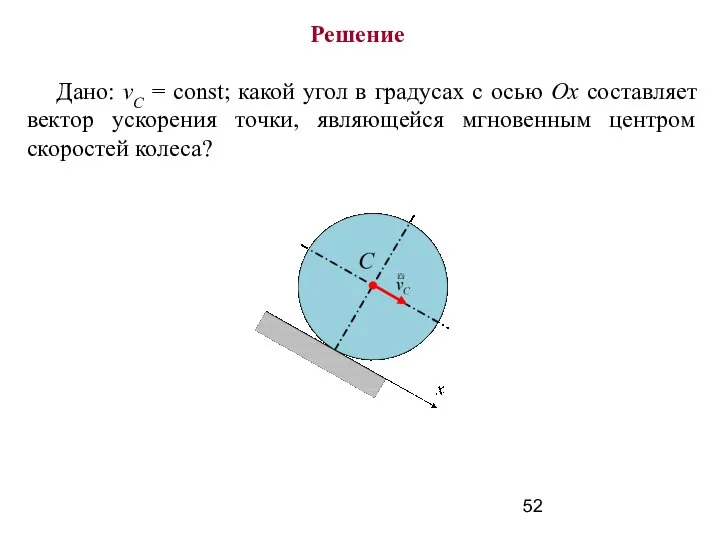
- 52. Решение Дано: vС = const; какой угол в градусах с осью Ox составляет вектор ускорения точки,
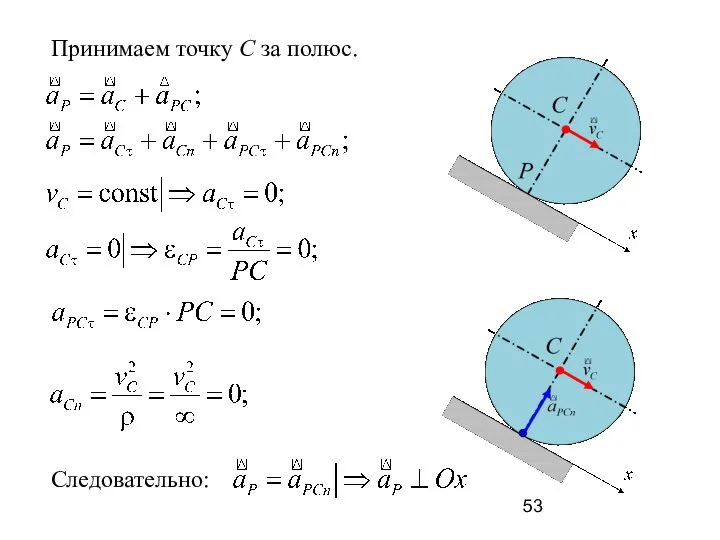
- 53. Принимаем точку С за полюс. Следовательно:
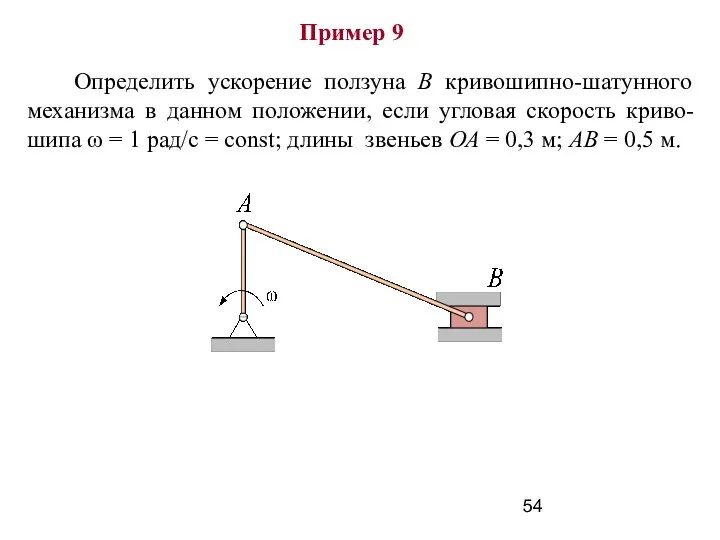
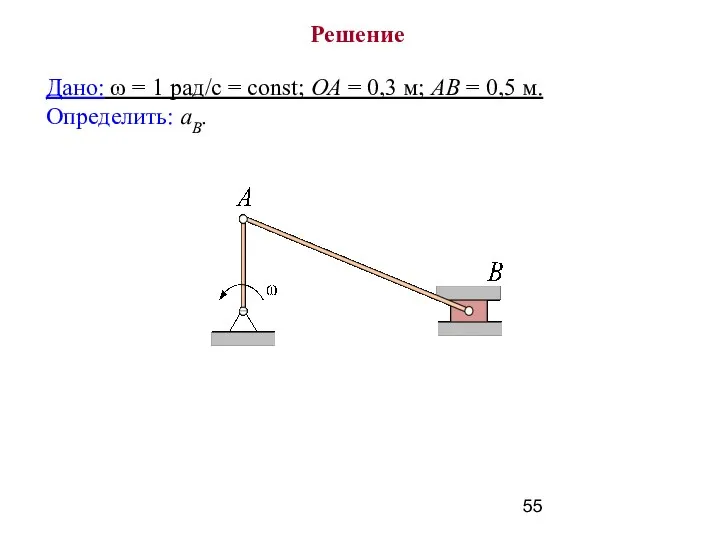
- 54. Пример 9 Определить ускорение ползуна В кривошипно-шатунного механизма в данном положении, если угловая скорость криво-шипа ω
- 55. Дано: ω = 1 рад/с = const; ОА = 0,3 м; АВ = 0,5 м. Определить:
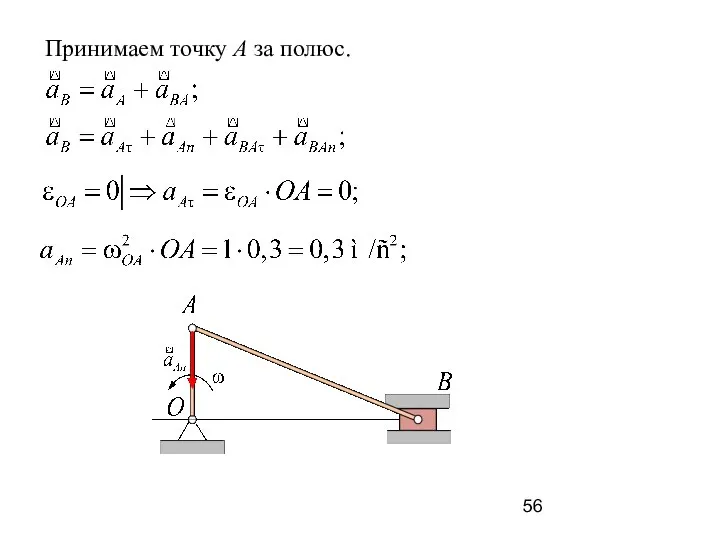
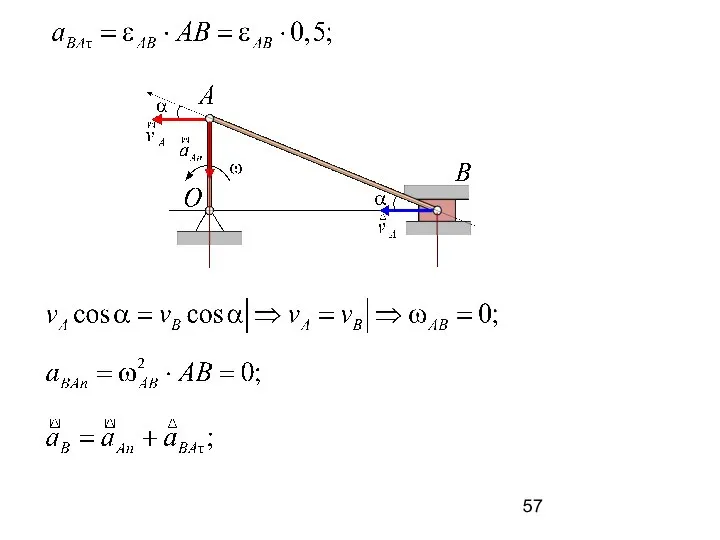
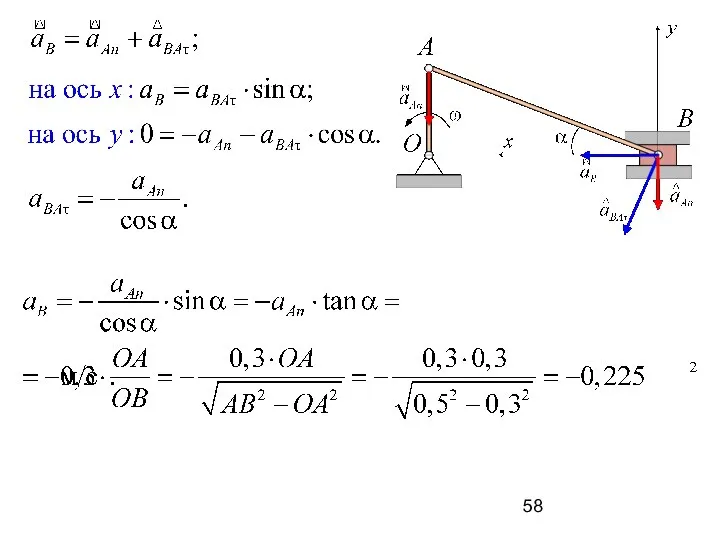
- 56. Принимаем точку A за полюс.
- 60. 5.1. В указанном на рисунке положении четырёхзвенника скорость и ускорение точки А кривошипа ОА равны: vA
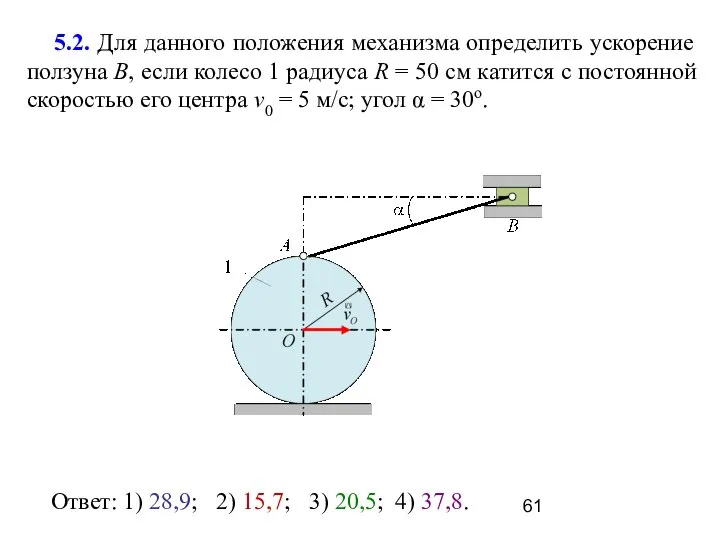
- 61. 5.2. Для данного положения механизма определить ускорение ползуна В, если колесо 1 радиуса R = 50
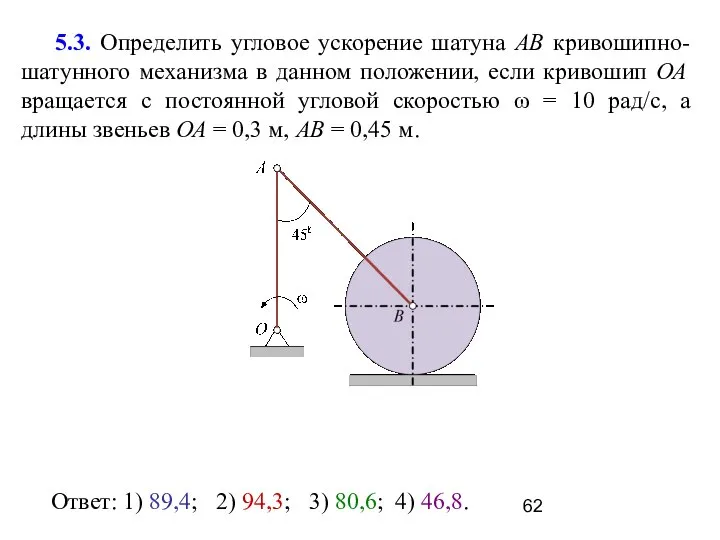
- 62. 5.3. Определить угловое ускорение шатуна АВ кривошипно-шатунного механизма в данном положении, если кривошип ОА вращается с
- 64. Скачать презентацию


















 Бумажная пластика - презентация для начальной школы
Бумажная пластика - презентация для начальной школы Издержки фирмы
Издержки фирмы Креативная парковая полоса
Креативная парковая полоса Культура Китая Выполнила Биер Анастасия ученица МОУ СОШ №13 10 класса
Культура Китая Выполнила Биер Анастасия ученица МОУ СОШ №13 10 класса Игры и развлечения на воде, применяемые на различных этапах обучения
Игры и развлечения на воде, применяемые на различных этапах обучения Презентация "Готический стиль" - скачать презентации по МХК
Презентация "Готический стиль" - скачать презентации по МХК Нормирование точности деталей вал и стакан цилиндрического двухступенчатого редуктора
Нормирование точности деталей вал и стакан цилиндрического двухступенчатого редуктора Загрязнения Каспийского моря нефтью и нефтепродуктами
Загрязнения Каспийского моря нефтью и нефтепродуктами Презентация на тему "Диагностика инновационного потенциала личности" - скачать презентации по Педагогике
Презентация на тему "Диагностика инновационного потенциала личности" - скачать презентации по Педагогике Разрезы (вырезы) на аксонометрических изображениях деталей. 8 класс
Разрезы (вырезы) на аксонометрических изображениях деталей. 8 класс Распространенные заболевания человека
Распространенные заболевания человека Тәулсіз қазақстанның сыртқы саясатының доктринасы
Тәулсіз қазақстанның сыртқы саясатының доктринасы Кривошипно-шатунный механизм
Кривошипно-шатунный механизм Сучасне теплове обладнання (Експрес-кавоварки)
Сучасне теплове обладнання (Експрес-кавоварки) Лекція 8. Українська культура другої половини XX століття
Лекція 8. Українська культура другої половини XX століття Історія української культури
Історія української культури Христианство. Распространение христианства в мире
Христианство. Распространение христианства в мире Существующие системы контроля технического состояния автосцепного устройства
Существующие системы контроля технического состояния автосцепного устройства Улан-Удэ, 2009. - презентация
Улан-Удэ, 2009. - презентация Резьба. Крепёжные изделия
Резьба. Крепёжные изделия КОВАЛЕВСКАЯ Софья Васильевна (1850-1891)
КОВАЛЕВСКАЯ Софья Васильевна (1850-1891) Турбо Паскаль
Турбо Паскаль Введение в религиоведение
Введение в религиоведение Разработка главных страниц и пользовательских элементов управления
Разработка главных страниц и пользовательских элементов управления Königsberger
Königsberger Проф. д-р Иван Козовски Управител на Медицински център за асистирана репродукция “Варна” ООД
Проф. д-р Иван Козовски Управител на Медицински център за асистирана репродукция “Варна” ООД Графические возможности яп VB
Графические возможности яп VB Композиционные и оксидные проводящие материалы
Композиционные и оксидные проводящие материалы